[Tutorial] Optimized Binary Lifting Technique

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
2	maomao90	163
4	atcoder_official	161
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	nor	153
9	Dominater069	153

Hello Codeforces!

Me and my friend JaberSH1 are glad to introduce this technique to the CP community since maybe only a few people know about it, personally me and Jaber worked on it and we haven't heard/read about such a thing before.

What can it do?

$$$K$$$-th ancestor & $$$LCA$$$ queries in $$$O(N*log(log(N)))$$$ preprocessing, and $$$O(log(log(N))$$$ per query.

Prerequisites:

Tree basics
Heavy-Light Decomposition
Binary Lifting

Ok let's get into it,

$$$K$$$-th ancestor queries:

Given a tree of $$$N$$$ vertices, let's build the HLD chains. For each chain, we are going to store its vertices in an array such that we can reach them by index. Let's take a vertex $$$u$$$, now we want the $$$K$$$-th ancestor of $$$u$$$. It's easy to look it up walking up the chains until we reach the chain with the maximum-depth top vertex for which its depth is less than or equal to $$$depth_u - k$$$. This operation costs $$$O(log(N))$$$ since we only change the chain we are in when the subtree size doubles up. Now imagine another tree containing only the light edges of our original tree, its depth is going to be less than or equal to $$$log(N)$$$. This is equal to adding $$$smart$$$ edges between the top vertices of the chains, each top vertex connected to the top vertex of the chain of its parent. See the picture below:

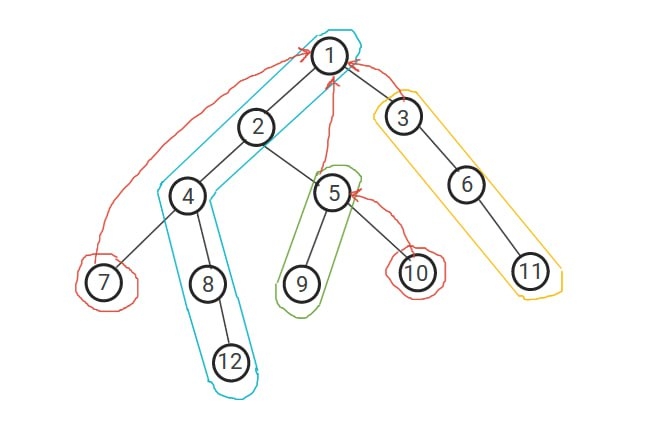
Let's build a binary lifting array over this compressed tree. Since its depth is not more than $$$log(N)$$$ then we will store only $$$log(log(N))$$$ info for each top vertex. Ok, now back to the $$$K$$$-th ancestor query, we can binary lift to the chain with the minimum-depth for which its depth is bigger than $$$depth_u - k$$$, this operation costs $$$O(log(log(N)))$$$. Our required vertex is going to be in the parent chain of this chain and we can reach it by index in $$$O(1)$$$.

$$$LCA$$$ queries:

Using the same technique, we can get the $$$LCA$$$ of two nodes $$$u$$$, $$$v$$$ in $$$O(log(log(n)))$$$ time complexity, we will store for each chain in the HLD tree the depth of the chain (how many chains above it), now if we consider node $$$u$$$ has a chain with higher depth than the chain of node $$$v$$$, we will try to lift node $$$u$$$ to be in a chain with the same depth of the chain of node $$$v$$$. to do this, we will have to find the chain with depth equal to the depth of the chain of $$$v$$$ plus $$$1$$$, and then we will go to the parent of the top node of that chain so now, node $$$u$$$ and $$$v$$$ have the same chain depths, and if they are in the same chain then it's easy to see that the higher node is the $$$LCA$$$. Otherwise, we will lift both chains of $$$u$$$ and $$$v$$$ as long as the head of the chains differ, after we lift the chains, the parent of the chain with the highest top node should be the $$$LCA$$$.

Jaber's code:

#pragma GCC optimize("O3", "unroll-loops")
#pragma GCC target("avx2", "popcnt")
#include <bits/stdc++.h>
// v.erase( unique(all(v)) , v.end() )    ----->   removes duplicates and resizes the vector as so
using namespace std;
#define IO_file freopen("output.txt","w",stdout), freopen("input.txt","r",stdin);
#define ll long long
#define lld long double
const lld pi = 3.14159265358979323846;
#define pb push_back
#define pf push_front
#define all(a) a.begin(),a.end()
#define rall(a) a.rbegin(),a.rend()
#define getunique(v) {sort(v.begin(), v.end()); v.erase(unique(v.begin(), v.end()), v.end());}
constexpr int mod = (int)(1e9 + 7);
#define log(x) (31^__builtin_clz(x)) // Easily calculate log2 on GNU G++ compilers
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
int rand(int x, int y) {
  return uniform_int_distribution<int>(x, y)(rng);
}
 
const int N = 2e5 + 1;
 
struct HLD {
  
  int n; // the number of nodes
  vector<int> sub, top, depth, parent, in, out, seq;  
  vector<vector<int> > adj;
  vector<int> dep; // for the lift tree
  vector<int> up[4]; // for the lift tree
  int tick;
 
  HLD() {}
  
  HLD(int n) {
    init(n);
  }
  
  void init(int n) {
    this->n = n;
    sub.resize(n + 1);
    top.resize(n + 1);
    depth.resize(n + 1);
    parent.resize(n + 1);
    in.resize(n + 1);
    out.resize(n + 1);
    seq.resize(n + 1);
    adj.resize(n + 1, {});
    dep.resize(n + 1);
    for(int i = 0 ; i < 4 ; i++){
      up[i].resize(n + 1);
    }
    tick = 0;
  }
  
  void add_edge(int u, int v) {
    adj[u].push_back(v);
    adj[v].push_back(u);
  }
  
  void build_HLD(int root = 1) {
    top[root] = root;
    depth[root] = 0;
    parent[root] = -1;
    up[0][root] = root;
    dfs1(root);
    dfs2(root);  
  }  
  
  void dfs1(int v) {
    if(parent[v] != -1){
      adj[v].erase(std::find(adj[v].begin(), adj[v].end(), parent[v]));
    }
    sub[v] = 1;
    for(auto &u : adj[v]){
      parent[u] = v;
      depth[u] = depth[v] + 1;
      dfs1(u);
      sub[v] += sub[u];
      if(sub[u] > sub[adj[v][0]]){
        std::swap(u, adj[v][0]);
      }
    }
  }
  
  void dfs2(int v) {
    in[v] = ++tick;
    seq[in[v]] = v;
    for(auto u : adj[v]){
      top[u] = u == adj[v][0] ? top[v] : u;
      if(top[u] != top[v]){
        dep[u] = dep[top[v]] + 1;
        up[0][u] = top[v];
        for(int c = 1 ; c < 4 ; c++){
          up[c][u] = up[c - 1][up[c - 1][u]];
        }
      }
      dfs2(u);
    }
    out[v] = tick;
  }
 
  // is u an ancestor of v ?
  bool is_ancestor(int u, int v) {
    return in[u] <= in[v] && in[v] <= out[u];
  }
  
  // kth ancestor of u
  int lift(int u, int k) {
    if(k < 0 || k > depth[u]) return -1;
    int t = top[u];
    if(depth[t] <= depth[u] - k){
      return seq[in[t] + depth[u] - k - depth[t]];
    }
    for(int c = 3 ; c >= 0 ; c--){
      if(depth[up[c][t]] <= depth[u] - k) continue;
      t = up[c][t];
    }
    t = up[0][t];
    return seq[in[t] + depth[u] - k - depth[t]];
  }
  
  // lowest common ancestor of u and v
  int LCA(int u, int v) {
    if(depth[u] > depth[v]) swap(u, v);
    if(is_ancestor(u, v)) return u;
    int tu = top[u];
    int tv = top[v];
    if(dep[tu] > dep[tv]) swap(tu, tv);
    if(is_ancestor(tu, tv)){
      for(int c = 3 ; c >= 0 ; c--){
        if(dep[up[c][tv]] <= dep[tu]) continue;
        tv = up[c][tv];
      }
      return parent[tv];
    }
    int k = dep[tv] - dep[tu];
    while(k){
      int c = log(k);
      tv = up[c][tv];
      k ^= (1 << c);
    }
    for(int c = 3 ; c >= 0 ; c--){
      if(up[c][tu] == up[c][tv]) continue;
      tu = up[c][tu];
      tv = up[c][tv];
    }
    return depth[tu] < depth[tv] ? parent[tu] : parent[tv];
  }
  
};
 
int main()
{ios_base::sync_with_stdio(0),cin.tie(0);
int n, q; cin>>n>>q;
HLD t(n);
for(int i = 2 ; i <= n ; i++){
  int p; cin>>p;
  t.add_edge(p, i);
}
t.build_HLD();
while(q--){
  int x, y; cin>>x>>y;
  cout<<t.LCA(x, y)<<'\n';
}
    return 0;
}

My code:

#include <bits/stdc++.h>
#define GO cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);
typedef long long ll;
using namespace std;
const int N = 2e5 + 50;
vector<int> adj[N];
int ST[N][4], par[N], depth[N], sz[N];
int ind[N], comp[N];
int dep[N];
vector<int> v[N];
int n, q;
 
void DFS(int u = 1, int p = 1, int d = 0){
    par[u] = p;
    depth[u] = d;
    sz[u] = 1;
    for(int v : adj[u]){
        if(v == p) continue;
        DFS(v, u, d + 1);
        sz[u] += sz[v];
    }
}
 
void DFS2(int u = 1, int p = 1, int c = 1){
    int mx = 0, nd;
    ind[u] = v[c].size();
    v[c].push_back(u);
    comp[u] = c;
    for(int v : adj[u]){
        if(v == p) continue;
        if(sz[v] > mx){
            mx = sz[v];
            nd = v;
        }
    }
    for(int v : adj[u]){
        if(v == p) continue;
        if(v == nd) DFS2(v, u, c);
        else{
            ST[v][0] = c;
            dep[v] = dep[c] + 1;
            DFS2(v, u, v);
        }
    }
}
 
int jump(int u, int k){
    if(!k) return u;
    if(k > depth[u]) return -1;
    if(ind[u] >= k) return v[comp[u]][ind[u] - k];
    k -= ind[u];
    u = comp[u];
    int dpt = depth[u];
    for(int i = 3; i >= 0; i--){
        int nC = ST[u][i];
        if(dpt - depth[nC] < k) u = nC;  
    }
    k -= dpt - depth[u] + 1;
    u = par[u];
    return v[comp[u]][ind[u] - k];
}
 
int LCA(int u, int v){
    if(comp[u] == comp[v]){
        if(depth[u] < depth[v]) return u;
        return v;
    }
    if(dep[comp[u]] < dep[comp[v]]) swap(u, v);
    u = comp[u];
    if(dep[comp[u]] > dep[comp[v]]){
        for(int i = 3; i >= 0; i--){
            int nU = ST[u][i];
            if(dep[nU] > dep[comp[v]]) u = nU;
        }
        u = par[u];
        if(comp[u] == comp[v]){
            if(depth[u] < depth[v]) return u;
            return v;
        }
        u = comp[u];
    }
    v = comp[v];
    assert(dep[u] == dep[v]);
    for(int i = 3; i >= 0; i--){
        int nU = ST[u][i];
        int nV = ST[v][i];
        if(nU != nV) u = nU, v = nV;
    }
    if(depth[u] < depth[v]) return par[u];
    return par[v];
}
 
int main()
{
    GO
    cin >> n >> q;
    for(int i = 2; i <= n; i++){
        int a;
        cin >> a;
        adj[a].push_back(i);
        adj[i].push_back(a);
    }
    DFS();
    DFS2();
    ST[1][0] = 1;
    for(int i = 1; i < 4; i++){
        for(int j = 1; j <= n; j++){
            int u = ST[j][i - 1];
            ST[j][i] = ST[u][i - 1];
        }
    }
    while(q--){
        int u, v;
        cin >> u >> v;
        cout << LCA(u, v) << '\n';
    }
    return 0;
}

Комментарии (20)

Показать архивные | Написать комментарий?

Hosen_ba

13 месяцев назад, # |

+18

Thank you,very interesting Technique.

→ Ответить

JaberSH1

+31

Khaled_Al_Awad

+14

Brilliant!! Thx for sharing.

Ayman-Al-Khatib

It's really great work. Thank you for your efforts.

Omar_Al_Midani

Great achievement!!

Go8

Thx for your effort. Great technique<3

AboModar

+12

very interesting thanks!

Chifwin

← Rev. 2 →

Interesting technique!

Also I checked your codes on judge.yosupo.jp: first, second and my template, so on tree n <= 5*10^5 simple binary liftings with tin\tout 1.5 times faster than yours( Maybe this can be optimized somehow?

UPD: you can try to send on this problem, there are 10^7 queries and intended solution is O(1) on query, maybe your also AC

13 месяцев назад, # ^ |

+28

Thank you!

Probably the implementation could be optimized further ig, thx for your feedback and testing!

Yes, it passed the second problem. Here's the submission: https://codeforces.net/gym/100091/submission/228193926

better.call.grizo

Thanks, I didn't know this before, I've solved many problems using this technique

Rj3i_Flicker

+21

Are you LGM guys ? Very brilliant idea

Aaeria

+19

Interesting idea, but don't stop there. Now you can use "Optimized Binary Lifting Technique" on your compressed tree.

joaozao

← Rev. 5 →

Very interesting!!

But, the preprocessing cost wouldn't be $$$O(n)$$$? Because you spend $$$O(n)$$$ to build the compressed tree, and then $$$+O(log(n)\cdot log(log(n)))$$$ to binary lift on it, which results in a total of $$$O(n)$$$ preprocessing and $$$O(log(log(n)))$$$ per query?

+16

In a worst case scenario the number of chains could be $$$N-1$$$ so it would cost $$$Nlog(log(N))$$$ to build the binary lifting array.

Hmmmmm, you are right, I'm confusing the number of chains with the height of the compressed tree

2147483648

This technique is well known in Russia (I'm not kidding).

Nice lol

I expected that somebody out there must've come up with this technique before us because it's really straight forward.

EyadBT

Could you maybe provide a link?

Well, during our university algorithmic course we once had a task (as a theoretical HW) to come up with solution to LA with $$$O(n\log \log n)$$$ preprocessing and $$$O(\log \log n)$$$ query time without using 4 russian method. Everyone came up to your's idea :D

X_01

these techniques are not easy to find or comes up instantly thanks for sharing

Блог пользователя EyadBT