Нужно сгенерировать координаты N (1 <= N <= 300) точек, таких что любые три точки не лежат на одном отрезке. Нужно что-бы координаты точек были не больше по абсолютной величине 10000.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
09:58:51
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
09:58:51
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 07:36:10 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Может быть так? Взять окружность с центром в 0,0 и радиусом r = 10000, затем точки размещать на окружности. Длина окружности π·10000·2 чего должно хватить для 300 точек. Так как все точки будет на окружности, то любая прямая максимум сможет пройти через 2 точки.
Я тоже так думал, но координаты должны бить целыми.
Может я конечно накосячил где-то, но моя программа насчитала лишь 4 целочисленных точки на этой окружности:
UPD. Все же накосячил. Исправил баг — 36 точек.
UPD2. Больше всего точек на окружности радиуса 5525 — 180 штук. Надо что-то похитрее, чем окружность придумать
Немного переделал эту программу. Она берет целочисленные точки с окружностей: http://ideone.com/ugQPuy
точки: (0,0), (1,1), (2,3), (3,6), (4,10), ...
UPD: да, ошибся, 300 в квадрат не умею возводить :D можно 4 ветви попробовать, но вроде тоже чуть-чуть не хватит
UPD2: 4 ветви, дают больше 300 точек, сделать все тоже самое, что написано, но в 4 стороны симметрично центра и не ставить нулевую точку
Согласен, такое решения тоже рассматривал.
Что мешает делать random? Проверка будет занимать N^2, генерировать N точек. Будет работать довольно быстро, примерно N^3 * sqrt(N)
Я не знаю как написать такую программу. Я думаю здесь есть более простое решение. По этому я написал в форум.
Полгода занимаетесь СП и даже не имеете представления, как это загуглить? Запущенный случай...
int n = 0;
vector<pair<int, int>> arr;
while (arr.size() < N)
{
int x = rand() % 20000 — 10000;
int y = rand() % 20000 — 10000;
if (check(arr, x, y))
{
}
}
check
int n = arr.size();
for(int i = 0; i < n; ++i)
{
for(int j = i + 1; j < n; ++j)
{
}
}
return true;
точОк :D :D
з.ы. простите
з.ы.ы. исправьте
Впервые узнали о существовании Украинского языка? То что CodeForces его не поддерживает ещё не значит что подобные нюансы достойны порицания :)
Казалось бы, совсем тупая задача.
Генерируем точки рандомно и добавляем их по одной во множество. При добавлении точки проверяем за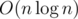 : не образовалась ли у нас тройка лежащих на одной прямой точек. Надеюсь, мне не нужно объяснять, как выполнить последний пункт?
: не образовалась ли у нас тройка лежащих на одной прямой точек. Надеюсь, мне не нужно объяснять, как выполнить последний пункт?
Рассмотреть две функции: y=sqr(x) задавать значения x [-100,100], и у=sqrt(x) задавать значения x [1,100] и добавить еще какую то точку, которая точно не будет принадлкжать или лежать на одной прямой с точками графиков, например (-1,-1).
Там нельзя дробные координаты, а sqrt даст только 10 таких на интервале
Во-первых 100, во-вторых я не прав со своим предложением
Параболу можно взять по простому модулю.
x = t, для t = 1, 2, ... N, N < p < 10000.
для t = 1, 2, ... N, N < p < 10000.
Очень красивая идея, спасибо за то, что поделились! Приму на вооружение.
Хотя я немного сомневаюсь, что автор топика сможет доказать тот факт, что у нас не будет трех точек на одной прямой для N < P.
Да, это правда! Я не могу понять и доказать эту формулу, но и Вы поймите меня: 1) Вы не учли разницу в веке и образовании ( Ilya_MSU — студент МГУ, я — ученик СОШ в Богом забитом в селении) 2) Ближайшей человек, который нормально знает програмирование находится в радиусе 100 км от меня. 3) Все что я знаю, я добыл на властном опыте!
Сразу признаю одну вещь: я повел себя слишком грубо и высокомерно.
Тем не менее, мне прекрасно видно, что Вы пытаетесь найти на все готовое решение. Даже скорее так: Вы не ищете его сами, а ждете, когда кто-то его Вам даст. Я считаю это ужасной вещью и начинаю злиться, когда кто-то себя так ведет. И я не считаю, что этому есть какие-то оправдания.
Хотя я сам себя веду как дурак: пытаюсь задеть Вас своими высказываниями, хотя мне хорошо понятно, что от этого никакого толку не будет. Ладно, в следующий раз вообще ничего не буду писать.
Я согласен с Вами. То что я пишу сюда это ужасно! Но я знаю, что пишу в форум только тогда, когда я УВЕРЕН, что не смогу решить задачу без стороной помощи. И то что Вы зашли на мой блог и дали ответ на любой вопрос это большой плюс. Ведь все что не делается, делается к лучшему. И по этому большое спасибо всем. :)
Вот это заявление. Совершенно не понимаю, что в этом такого сложного.
Пусть оказались на одной прямой.
оказались на одной прямой.
Это значит, что (распишем равенство векторного произведения нулю): .
.
Чтобы не возиться со взятиями остатка по модулю, даже ослабим утверждение. Запишем, что левая и правая часть не равны, а сравнимы по модулю p, тогда можно внутренние взятия остатка убрать:
Сократим обе части на (b - a)·(c - b) (так как мы брали разные a, b и c в пределах, скажем, от 1 до N < P, то это выражение не равно нулю).
Надеюсь, это поможет автору топика.
Формула интересная, но чекер нашел где-то ошибку в формуле. :(
У Вас есть чекер, который может находить ошибки в формулах? о_О
Все спокойно заходит на Accepted.
Я кинул решение на acmp, то программа падает на 11 тесте. И я все делал по формуле и учел, что p — простое число, которое больше N.
Речь наверняка идет об этой задаче. Просто на будущее: на том сайте есть обсуждение к каждой задачке и часто там уже написаны решения(как например в этом случае) и можно не создавать для этого тему отдельно здесь.
да, но
здесь есть прямой эфир, а значит ответят очень быстро
здесь больше красных, которые могут посоветовать простые идеи (см. выше)
Можно просто сгенерировать в несократимые дроби знаменатель и числитель которых не превышают 25, отсортировать их и потом написать что-то такое:
Заметим, что полученная функция выпукла. В А хранятся отсортированные несократимые дроби.
У меня такое зашло.
Upd Чуть-чуть изменив это решение мне удалось сгененрировать более 2400 точек, соответствующих условию задачи. Код.
Или вот такое. Тоже очень простое в реализации и для понимания. И тоже Accepted. Мы просто строим две вот такие функции:
~~~~~
cin >> n; cout << "YES\n"; flag = true; k = 1; x = -10000; y = -10000; while (n != 0) if (flag) { printf("%d %d\n", x + 10000, y); n--; flag = !flag; } else { printf("%d %d\n", x, y); flag = !flag; y += k; k++; x++; n--; }Большое спасибо. Не понятно почему все мои (и не только) алгоритмы не проходили 11 тест.
Ворс плохого не посоветует. ;)
Ворс молодец, Ворс хорошие графики принес посмотреть...
Почему в 3м лице о себе?
Да, тут целое соревнование для марафона: кто больше точек вместит в квадрат:)
Парабола
Попробовал решить с помощью вычисления комплексных корней из -1. Берём N корней из -1 и размещаем на окружности радиусом 9000
Для N <= 300 работает без проблем, но уже при N=400 появляются точки на одной линии.
Можно вместо корней из минус единицы брать точки вида (round(R cos x), round(R sin x)) при целых x от 0 до n - 1 и R = 10000. Работает примерно с таким же эффектом (т. к. такие точки приблизительно равномерно распределены по окружности при больших n), где-то до n = 375.