I cannot optimize this code anymore. Please let me know how to optimize.
Thanks in advance. My Code
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
I cannot optimize this code anymore. Please let me know how to optimize.
Thanks in advance. My Code
| Name |
|---|



Although I haven't got AC yet, I have learned something to optimize. Thanks
In constant optimisation problems, especially in those which have enormous input data, it is good to write your own function for scanning integers. Below is the procedure i have used in many problems:
The most significant thing you need to optimize is storing the result of base^2,base^4,base^8.... So when calculating base^n you can just multiply the corresponding power of twos like base^7 = base * base^2 * base^4
Nobody has really helped you, but your post got
-8rating. Codeforces community is so awful...In fact, if you have an N × N matrix (let's call it M), it's possible to calculate ME × V (V is a vector) in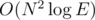 , not in
, not in 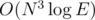 . To do so, you need to precalculate M1, M2, M4, M8.... Then, if you need to calculate, for example, M13 × V, you can just use the following formula: M13 × V = M8 × (M4 × (M1 × V)).
. To do so, you need to precalculate M1, M2, M4, M8.... Then, if you need to calculate, for example, M13 × V, you can just use the following formula: M13 × V = M8 × (M4 × (M1 × V)).
Sorry for my pidgin English, but in Russian (my native language) I'd explain this exactly the same way.
UPD. With this idea I instantly got AC in Java in 2.7s without any additional optimizations.
Nice trick, didn't know about it before :)
AlexanderBolshakov , I always become happy when I learn a new thing. This is a very good idea. Got AC in 2.15s. Thanks :)
Code
AFAIK, calculating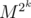 from
from 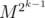 will take
will take 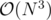 .
. 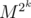 until
until 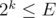 , won't the precalculation itself take
, won't the precalculation itself take 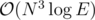 ?
?
so if we continue calculating
Yes, the precalculation takes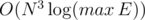 . But in such problems this time is negligible, because the precalculation is performed only once, but calculation of ME × V — many times.
. But in such problems this time is negligible, because the precalculation is performed only once, but calculation of ME × V — many times.
i understand now. there are multiple queries, each with different value of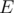 .
.
thanks for ur help! :)
I got AC with a 3x3 matrix and optimizations, but I heard that there is a way of doing with just a 2x2 matrix. Can someone tell me how to find this 2x2 matrix?
PROBLEM: G(n) is defined as G(n) = G(n-1) + f(4n-1) , for n > 0 and G(0) = 0 f(i) is ith Fibonacci number. Given n you need to evaluate G(n) modulo 1000000007.
MY SOLN: use/prove: G(n) = f(2n) * f(2n + 1),
FOR EXTRA SPEED: use the following recurrences:
f(2n) = f(n)[2*f(n+1) – f(n)],
f(2n + 1) = f(n)^2 + f(n+1)^2
Nice! Fibonacci has so many interesting properties, it doesn't stop to amaze me.
For this problem I used the idea that G(n) = 7*G(n-1) — G(n-2) + 1 I don't know how to prove it, but it works.
Submitted in one GO without extra speed. Just tell me how u got the relations for extra speed
Link To Solution -> Code
Passed in 0.10 sec