Hello everybody,
I was solving last year's IOI problem Game. In short, you are given an initially empty grid and the problem consists of answering queries "Update element in cell x,y" and "Get GCD of all elements in rectangle x1,y1~x2,y2". Note that the grid is huge (10^9 x 10^9)
If it is solved using 2D segment tree it is pretty straightforward, however reading Bruce Merry's post about it, he suggest that there is more efficient (though harder to code) implementation using balanced binary trees. Obviously 2D segment tree would take O(logR*logC) time and memory per query (R,C are the sizes of the grid), however according to his post you can do it in O(logNu*logNu) time per query (Nu is the number of update operations) and significantly less memory.
I can code and understand how to do it in 1D using balanced binary tree, but I can't seem to find a correct way to extend it into higher dimensions. Can anyone explain how would the given problem be solved using balanced binary trees (not segment trees) ?
Thank you in advance,
Enchom
If I truly understand bmerry, he advised to implicitly build a huge O(N * R) segment tree using the following idea: if some node doesn't exist, it is treated as being completely filled by zeroes. During each update, we'd create at most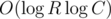
new nodes. Am I right?
If so, you can just replace the 1D segment trees of the second dimension with binary search trees and get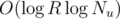
time and 
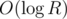memory per query.
But I still don't know how to solve this in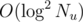
per query.
Well yes but I can't seem to understand what will be technique exactly? Like if you replace the 1D segment trees with binary search trees, what exactly do you keep in your segment tree?
And yea, he seems to be talking about some way to replace both segment trees with binary search trees.
In a vertex corresponding to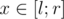
we store all elements of our 2D array with x from this range, sorted by y.
I understand it, but I still don't know how to do this (at least, easily) :).
Aha, I understand it now, so it really turns out to be O(logR) memory per query, which will be sufficient to solve it (as 2D segment failed memory limit on last subtask). Thank you very much!
If someone, however, knows what bmerry meant, i.e. how to replace both segment trees, it'll be wonderful to share the knowledge :)
It'd be great :).
P.S. I've just remembered that it's possible to solve this problem with a k-d tree in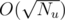
.
O(sqrt(Nu)) memory or time per query?
Time. The memory will be O(Nu).
And I forgot that we'd need to build a k-d tree online. I don't know how to do this.
I can't actually remember what I was thinking when I wrote that post, but I think I probably had in mind only replacing the inner dimension with binary search trees. Rebalancing operations in the outer dimension would just be too expensive.
With balanced binary trees in the inner dimension, it would require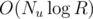
memory. It's nasty to implement because the rebalancing operations need to recompute GCDs for internal nodes, which rules out using an off-the-shelf balanced binary tree like std::map.
It might also be possible to solve the problem using segment trees with a higher branching factor to reduce the height of the tree, at the cost of most expensive queries. I haven't worked through the calculations about exactly how much memory is used, however.
I think it's OK, because when you calculate gcd of n numbers, straightforward implementation works in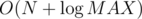
, not in 
.
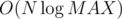I think that each rebalancing would take
, because you need O(N) operations to merge 'values' (which are trees themselves) of two nodes, don't you?
Thank you very much for the explanation. My friend Hristo Venev got full score on the competition itself by compressing chains of nodes, so that works too, though I don't like it. I will try to code the solution you described by making the inner structure Treap :)