How can I find modular multiplicative inverses of a range in linear time?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 19:18:17 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Do you want to find a multiplicative inverse for all numbers from 1 to N — 1?
It can be easily done for a prime N, the idea should be obvious if you'll read about primitive roots modulo N.
For non-prime N the idea should also be similar.
I read about primitive roots that -
If the prime number is p, a primitive root g is a number, that when n goes from [1...p - 1], then gn mod p goes through all the numbers [1...p - 1] in some order.
How do I utilize this further? Sorry but I am unable to really understand how to form a relation between modular inverse and primitive root.
If you thought harder, you'd come up with an idea :).
Due to Fermat's Little Theorem: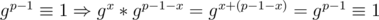 .
.
if the number with respect to which you are finding the modular inverse (i.e. the 'M' in A%M is prime)you can use the Fermat's little theorem according to which the modular inverse of a number with respect to a prime number (say A and P respectively) is pow(A,P-2)
so in one for loop you may find the modular multiplicative inverses of the numbers in the range but the complexity is O(nlogp) as the power function takes log(p) time
http://e-maxx.ru/algo/reverse_element#4 (it's in russian but you can see the code)
Can you please explain the last step before QED in the proof provided?
What have they done after taking mod m on both sides?
They've multiplied both sides of the equality by
r[i] * r[m mod i].