Hello everybody,
Recently I was solving a problem with queries on a tree and I stumbled upon Heavy-Light Decomposition. I read this article and understood the concept, then coded the solution itself. However, I noticed that for the proposed problem in the article — Dynamic distance query, they say it could be solved in O(logn) per query, while I can't see how to improve the O(log^2) bound. The article says
"It might seem that we have to ascend logarithmically many heavy paths each of which takes logarithmic time, but this is not the case; only the first one, if we start out on it, has to take logarithmic time to query; for the others, which we skip over in their entirety, we can just look up a variable indicating the sum of all weights on that path"
However I don't think this is true. When going up the tree you don't have to necesserily skip entire paths, it might turn out that each heavy path you stumble upon, you start from somewhere in the middle of it, and therefore have to perform a query in the corresponding segment tree. I was wondering if I am missing something or the article isn't entirely correct?
Thanks in advance!










Sounds like you might be leaving the path in the middle all the times but you enter a path in the middle at most once. Can't prefix sums help you then?
yes, but you have update operation too, so how do you keep prefix sums efficiently?
Sorry, my miss, didn't read it carefully and did not see that there is an 'update' operation there. Having this one I would agree with your question.
Yeah, in order to have an solution using HLD, we'd need a "dynamic prefix sums" structure with O(1) complexities of query and update.
solution using HLD, we'd need a "dynamic prefix sums" structure with O(1) complexities of query and update.
Does such structure exist with O(logN) complexity per update?
Since you update only one heavy path, so it doesn't have to be constant.
I might be wrong again in this topic but isn't it only the query operation required to have O(1) complexity? It seems to be ok to have complexity O(logN) for the update because we always update only one path.
Uh, right, just logarithmic per update. Still, I don't know any such structure.
Well I suppose such structure doesn't exist or is way too difficult to implement (with large constants possibly), else we would use it instead of BIT everywhere.
I think that a possible o((N+Q+M) log N) solution (Q = queries, M = modifications, N = number of vertices of the tree) may be the following:
You have at most log N heavy paths. So you can store for each heavy edge E, the heavy paths H(E) such that if you are standing at the root of any of the H(E) heavy paths and you want to go to the root you have to traverse the edge E. Then whenever you update an edge in the heavy path that contains E and in E or a closer to the root edge, you also make the update in all the H(E) heavy paths.
Let's define H in a more formal way. If A-B is an edge, and A is closer to the root than B, then we associate B with that edge (as B has only one parent but A may have more than one child). Let's call that edge E[B]. If E[B] is heavy then there exists a heavy path that uses A-B. Let's say that the path is for example X-Y-A-B-C-D. Then we use a BIT to store the values of the edges X-Y, Y-A, A-B, B-C and C-D. We also add an edge R-X (R for root), and we store that value outside the BIT. R-X will be the path from X to the root only considering the weights of the heavy edges (that is, the weight of the path to the root if we modify the light edges to have weight 0).
Now we calculate H as follows: We enumerate the BITs that store the heavy paths as follows: Heavy[0], Heavy[1], Heavy[2], ... and for each node T we store in H the indexes of the BITs that correspond to the heavy paths that are below T. We can do it recursively as follows (it's pseudocode, not code):
And we call fillH(root).
Then we ignore H for the light edges. Now we must fill the R-X edge for each BIT. We can do it as follows:
and we call this for each 0 <= BITNumber < NumberOfHeavyPaths
Then every time we make an update to a heavy edge, we search for the heavy paths that are below that edge and update that value as follows:
and now the query is just asking for the light edges, for the first heavy path, and for the RX edge of that path.
I hope you all understand this solution, if needed I can write code and post it here.
Wow, that's a very interesting way of doing it. I'm sure that the article didn't mean that but it really seems to be O(logN) per query! Great job!
Why is there at most log N heavy paths? For instance, every edge of perfect binary tree is light.
And it has logarithmic height.
I still don't understand why there are at most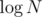 heavy paths. Can anyone enlighten me?
heavy paths. Can anyone enlighten me?
Let F(x) be the maximum amount of successive heavy paths in a tree of size x. The condition for an edge (u, v) to be light is that v's subtree is no more than half the size of u's subtree, so the amount of heavy paths in a single traversal from the root downwards will be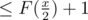 . This means we will encounter at most log(N) heavy paths in one query.
. This means we will encounter at most log(N) heavy paths in one query.
But doesn't this just show that in a particular path there are at most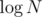 heavy paths involved? There can still be more than
heavy paths involved? There can still be more than 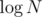 heavy paths in the entire tree.
heavy paths in the entire tree.
You change a maximum of log N paths while going from any vertex to a leaf, because when you change a path, you did not choose to go to a heavy child, so the current subtree size of the child must be less than that of the heavy child. So by changing a path, you reached a vertex that has at most half the subtree size of it's parent. So, after at most log N changes, you'll reach a leaf in the tree. Hence, any path in the tree can be traversed by changing at most O(log N) paths.
Yes, there are at most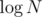 heavy paths and
heavy paths and 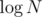 light edges in any single path from root to leaf. However, if I understand correctly, ltaravilse claimed that there are at most
light edges in any single path from root to leaf. However, if I understand correctly, ltaravilse claimed that there are at most 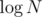 heavy paths in the entire tree, and this claim is essential for his algorithm to run in
heavy paths in the entire tree, and this claim is essential for his algorithm to run in  time per update.
time per update.
My explanation above was kind of short and not clear at all. Let me rephrase my idea.
Successive heavy paths will be connected by light edges, and the condition for an edge (u, v) to be light is that v's subtree is no more than half the size of u's subtree, so the amount of heavy paths in a single query will be logarithmic.
Of course, this doesn't mean that the total amount of heavy paths in the tree will be logarithmic. We can construct a tree like this...
and for a tree of size 2501, we will have 500 heavy paths, which clearly isn't logarithmic. However, we will only find one heavy path in a single traversal to the root.
I know that for normal heavy-light decomposition, the amount of heavy paths involved in a single query is logarithmic. Since query on a single heavy path takes time, therefore a single query in heavy-light decomposition takes
time, therefore a single query in heavy-light decomposition takes 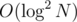 time in the worst case, which is not optimal. (Link-cut tree can perform query and update in
time in the worst case, which is not optimal. (Link-cut tree can perform query and update in  armotized time per operation.) So Enchom asked how to improved heavy-light decomposition to perform query and update in
armotized time per operation.) So Enchom asked how to improved heavy-light decomposition to perform query and update in  time.
time.
ltaravilse proposed an algorithm that claims to perform query and update in time per operation. However if I understood correctly, this time complexity relies on his claim that there are at most
time per operation. However if I understood correctly, this time complexity relies on his claim that there are at most  heavy paths in the entire tree, which I think is not true. Hence my question.
heavy paths in the entire tree, which I think is not true. Hence my question.
Ahhhh, sorry, I misunderstood the question then.
Anyway, are you sure he is claiming that there are log(N) heavy paths in the entire tree?
That claim, as I showed above, is clearly not true, unless he is talking about a specific problem with some special tree properties.
You can read his comment above and interpret it yourself.
Yes, I think he meant that. Anyway, I'm pretty sure we can still manage to get O(logN) per query and update, even if the amount of heavy paths is in the order of O(N).
In addition to the usual BIT, let's keep for each heavy path the following values: sumh = total sum of edges' values of the path h, globalh = sum of global updates to the path h (updates that cover every edge of the path), lengthh = amount of edges in the path h. Then, we'll have the following operations...
Since there will be at most two heavy paths we need to query/update partially for every query or update, we'll perform up to O(logN) constant operations and only two O(logN) operation, making the updates and the queries O(logN), unless I'm messing up somewhere.
Why is there at most one heavy path we need to query/update partially for every query or update?
Only the first and last heavy path may need to be updated partially, all other heavy paths in the middle will be traversed entirely, so the update will be global to those paths.
I don't think this is true. As OP said, "When going up the tree you don't have to necesserily skip entire paths, it might turn out that each heavy path you stumble upon, you start from somewhere in the middle of it, and therefore have to perform a query in the corresponding segment tree."
Yes, you're right about that. Sorry for messing up, my solution won't work then.
I know this post is about heavy-light, but this problem looks a lot easier to solve without it.
When you change edge from x to x's parent and increase it by d, what you are doing is increasing "distance to root" by d for every vertex in x's subtree. So you can keep the distances to root in pre-order, and update them using a BIT.
Haha, simple solutions are the best. Even though HLD+BIT is just 1 DFS (constructing the paths) and a while-loop for update/query, this is probably even easier to code. Now, this question is really just about the method described in the article, not about the problem in general.
I wonder if I've ever used subtree-path duality to get rid of the log-factor of BIT, though. My most recent (Yandex Algorithm round 2) binsearch+BIT with complexity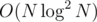 seems to work in 60 ms for N ≤ 5·104, that's insanely fast... and I don't remember ever getting TLEs due to the log-factor of BIT.
seems to work in 60 ms for N ≤ 5·104, that's insanely fast... and I don't remember ever getting TLEs due to the log-factor of BIT.
The link-cut tree paper ("A Data Structure for Dynamic Trees", Sleator and Tarjan 1982) uses biased binary search trees to get from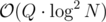 down to
down to 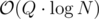 . The same concept can be aplied to the special case of a static heavy-light decomposition, using static binary search trees.
. The same concept can be aplied to the special case of a static heavy-light decomposition, using static binary search trees.
Cool, but I don't see the connection to the topic discussed here. Is it a better method than ffao's subtree-path duality + BIT one? How is it related to the question in the OP?
It's just a way to get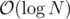 time per query for heavy-light decomposition. I cannot make any judgement about whether it is "better" (for any given definition of goodness) than some other proposition, because I haven't tried any.
time per query for heavy-light decomposition. I cannot make any judgement about whether it is "better" (for any given definition of goodness) than some other proposition, because I haven't tried any.
For me, better means "I'd prefer coding this during a contest, because it'd probably yield the most points". It's good if a code contains as few important ideas as possible (lower chance of a wrong / loose idea), as few risky places (possible problems with memory, overflow, mistakes in +-1s, too many / too long copypastas...) as possible, well-known structures or those I remember how to code exactly are better than pre-coded or longer / trickier ones, and last but not least, general time expected for writing the code.
Also, the "compatibility" of the person in question with the following type of problems — it's all subjective, anyway. And I'm skipping here mental state, past experience, type of contest, goals in the contest (points / experience / trying out new approaches...) and intuition, and maybe some more :D
I think it's safe to say that most of theoretical computer science does not care about implementation concerns, so when I refer to a paper, I don't offer a competitive programming-type solution. I'm offering background information, ideas, proofs and further theoretical reading on the subject, because those are harder to come by than implementations.
you can try divide and conquer and for query(left,right) build virtual tree with node in this intervals..
it is O(Q*log(Q))..
Can you please provide an example problem and solution/reference?