Given $$$N$$$ integer intervals $$$[a, b]$$$, find the maximum number of pairs of overlapping intervals where each interval can belong to at most one pair.
Two intervals overlap if they share a common point, including closed endpoints.
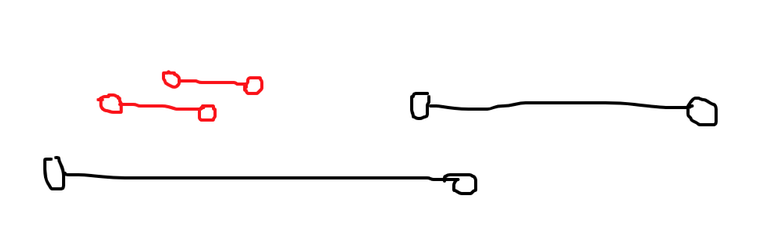
The answer to the example above is 2. Pair the 2 black intervals and the 2 red intervals together.
What is the best time complexity that can be achieved for this problem? Currently I'm not sure if it's even solvable in polynomial time.










maybe give some constraints genius, but i can do O(n log n) i thonk
You can do it in n*log(n). Sort the endpoints and process them from left to right. When a segment is ending, if it doesn't have a partner yet, this is your last chance to match it, so you might as well try. Among all unmatched open segments, pair this one with the one who ends first.
You can use an exchange argument to show this will always give you the best answer. I'm not sure if it's possible in linear time, but my gut says no.
a really nice question can be made from this concept, try contributing this question to leetcode or codeforces, nlog(n) is the best approach i could come up with thanks to @SecondThread
Question is similar to cses problem Room allocation. expected time complexity is O(nlogn)