Sieve of Eratosthenes used to determine prime numbers. A bool array in taken and initialized to false
first of all it starts with 2 and updates index of bool array of all multiples of 2 to be true..
like 4,6,8..but not 2 which is kept false. next false number is picked which is 3..and all its multiples are updated true like 6,9,12,15...updated true but 3 is kept false
similarly it is followed..
all numbers in the end which are false are primes.
then next false number is picked
int main() { static bool b[100000];
for(int i=2;i<=30000;i+=1)
{
if(!b[i])
{for(int j=2;j*i<30000;j++)
{
b[i*j]=true;}
}
} for(int i=2;i<30000;i++)
{
if(!b[i])
{
printf("%d",i);}
}
return 0;
}











We can reduce the number of iterations.
We only need to iterate i from 2 to sqrt(N), where N is the upper bound.
And j can start from i.
Check this code.
This is because any composite number has a divisor that does not exceed its square root.
(proof: Let n be a composite. There exists a, b (1 < a <= b < n) s.t. a*b=n. Then a must be less than or equal to sqrt(n))
Actually it's not the asymptotic optimization.
What is asymptotic optimization?
Sieve of Eratosthenes works in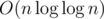 your optimization don't make it better.
your optimization don't make it better.
I just said we can reduce the number of iterations. I didn't say I optimized it nor my code has better time complexity.
Your code is not really most optimized. See my code: http://pastebin.com/fi2f9HCN
Could you tell me which part is different?
I used j+=i instead of j++ in
for (int j=i*i; j<N; j+=i)And because global array is initialized by zero, I named my array NonPrime instead of IsPrime to avoidfor (int i = 1; i <= N; i++) is_prime[i]=1;.P/S: I got TLE in one problem use this sieve. By a trade-off between readablity and performance. My following code run faster 3x.
First loop means we remove numbers 6k, 6k+2, 6k+3, 6k+4. Second loop means we try to iterate 5, 7, 11, 13, 17, 19, ... (6k-1 and 6k+1)
I got it. Thanks!
If you just want to generate prime number in [1,n], you can try this simple algorithm. It's running time is O(n).
your suggestions are welcomed. Guys i am just beginner programmer.This is my very first post.It may not be best solution but i posted it for beginner programmers(easy to understand) and my future reference.
Thanks for your suggestions in the matter.
:D :D