Покрывающий прямоугольник минимальной площади

10 лет назад, # |

+10

Если у нас есть выпуклая оболочка множества, то достаточно строить прямоугольники только на отрезках этой оболочки — ориентация подходящего прямоугольника будет совпадать с ориентацией какого-то из отрезков оболочки, и одна из его сторон будет содержать этот отрезок.

При указанных ограничениях это дает несложное решение за N^2 — O(N) кандидатов и проверка каждого наивным перебором за О(N).

→ Ответить

adamant

10 лет назад, # ^ |

А быстрее можно? :)

И как доказать факт про выпуклую?

→ Ответить

10 лет назад, # ^ |

← Rev. 2 →

Можно и быстрее; для заданного выпуклого многоугольника покрывающий прямоугольник минимальной площади можно найти за линейное время. Аналогично поиску диаметра этого многоугольника с помощью rotating calipers, только теперь нам нужно поддерживать две взаимно перпендикулярные пары rotating calipers вместо одной. А дальше аналогично — рассматриваем критичные углы для каждой из касательных, выбираем минимальных из четырех, поворачиваем...

По поводу доказательства — никогда не интересовался доказательствами, если честно:) Подозреваю, что его можно найти в любой фундаментальной книге по геометрии, вроде Препараты/Шеймоса) Или даже доказать самостоятельно, если немного подумать)

→ Ответить

10 лет назад, # ^ |

Что-то не вижу задачи в книге Препарата и Шеймоса(

→ Ответить

10 лет назад, # ^ |

← Rev. 3 →

-8

Факт не совсем верен. Верно, что оптимальный прямоугольник таков, что либо два из его углов совпадают с двумя противоположными вершинами выпуклой оболочки, либо на одной из его сторон лежит одна из сторон выпуклой оболочки.

В этом легко убедиться, если предположить, что на каждой стороне по одной точке и покрутить прямоугольник. Тогда площадь прямоугольника будет меняться, как произведение двух каких-то синусов (на константу), а произведение двух каких-то синусов — это, в свою очередь, сумма каких-то синусов/косинусов. Косинусы и синусы — выпуклые функции (в определённых рамках, конечно), значит, их сумма тоже выпукла, а значит, минимум достигается на границе интервала, то есть, когда они из сторон прямоугольника упёрлась в ещё одну вершину выпуклой оболочки.

→ Ответить

adamant

10 лет назад, # ^ |

Из первого не следует второе? Оо

→ Ответить

10 лет назад, # ^ |

Что первое, что второе?

→ Ответить

adamant

10 лет назад, # ^ |

Отвечал к первой версии правки)

→ Ответить

10 лет назад, # ^ |

два из его углов совпадают с двумя противоположными вершинами выпуклой оболочки — при этом все равно какая-то из сторон оболочки будет лежать на одной из сторон прямоугольника.

Если нет — значит, можно еще "покрутить" и уменьшать площадь (согласно рассуждениям, которые ты сам написал в следующем абзаце) до тех пор, пока не упремся в еще одну вершину, а из выпуклости оболочки следует, что мы при этом полностью накроем какую-то сторону этой оболочки.

→ Ответить

10 лет назад, # ^ |

Если два противоположных угла попали в вершины, то мы вылезем за рамки, в которых функции выпуклые.

Кстати., даже если только один угол прямоугольника попал в вершину выпуклой оболочки, то всё равно можем вылезти. Например, если рассмотреть треугольник со сторонами 1000, 1000, 1.

→ Ответить

10 лет назад, # ^ |

Что не так с этим треугольником? У меня плохо с воображением)

На всякий случай погуглил, пишут что указанного мною условия достаточно.

→ Ответить

10 лет назад, # ^ |

Да, я что-то затупил, извиняюсь.

→ Ответить

10 лет назад, # ^ |

"В этом легко убедиться, если предположить, что на каждой стороне по одной точке и покрутить прямоугольник. " — Что понимается под кручением прямоугольника? Судя по всему, это не поворот, ведь предполагается, что его площадь будет изменяться.

→ Ответить

10 лет назад, # ^ |

Да, имеется в виду поворот всех прямых содержащих стороны прямоугольника, относительно вершины выпуклой оболочки, через которую она (сторона) проходит. Четыре новые прямые по-прежнему образуют прямоугольник, поскольку это по-прежнему две пары параллельных прямых, перпендикулярных друг другу (в смысле, прямые из разных пар перпендикулярны друг другу).

→ Ответить

10 лет назад, # ^ |

Хорошо, тогда что понимается как "произведение 2 синусов"?

→ Ответить

10 лет назад, # ^ |

← Rev. 4 →

если рассмотреть отрезок (пусть его длина l) между двумя противоположными вершинами, в которые упираются стороны, то ширина полосы, в которую он влезает равна l·sin(α), где α — угол наклона между прямыми и этим отрезком. Так же и с другим аналогичным отрезком. Ну а площадь прямоугольника — произведение двух этих ширин. При этом угол наклона к прямым у двух отрезков отличается на некую константу.

→ Ответить

10 лет назад, # ^ |

Ага, теперь понятно. Только вот там дальше не все так просто. "Косинусы и синусы — выпуклые функции (в определённых рамках, конечно), значит, их сумма тоже выпукла, а значит, минимум достигается на границе интервала," — не факт, что рамки, в которых сумма синусов и косинусов выпукла, содержат в себе границы, в которых можно менять угол α, и нет гарантии, что минимум действительно достигается на экстремальном значении α

→ Ответить

10 лет назад, # ^ |

← Rev. 4 →

Если угол между этими отрезками составляет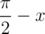 $\text{[math]}$ , α, то (опустив константу) получаем, что 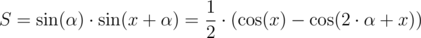$\text{[math]}$ . cos(x) — константа, α меняется в промежутке [L, R], где 0 ≤ L ≤ R ≤ π. При этом 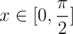$\text{[math]}$ . Таким образом, функция - cos рассматривается только на промежутке 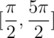$\text{[math]}$ . Чтобы функция была на этом отрезке выпукла, надо немного получше ограничить α...

→ Ответить