(When discussing, problem setter think his program have error middle result because of "Numerical instability"(may refer to floating error?), but I think this is an algorithm error, and the realization of me and Rainbow_sjy is hacked at local by myself when choosing the same seed)
Specifically, for the minimum circle coverage, we have that if $$$p_i$$$, $$$p_j$$$, and $$$p_k$$$ are the three points of $$$C_{res}$$$, then for a $$$p_{k'} \not\in C{res}$$$, there is a conclusion that $$$p_k \in C_{p_k',p_j,p_i}$$$ (Note that we have the condition $$$p_i \not \in C_{k,k',j},p_j \not \in C_{k,k',i}$$$).so the new circle can cover all the original points.But for this question, we do not have such a conclusion.
For example, when
R77=Circle((231850.00,887100.00),247424.00000000)
R31=Circle((145307.00,741503.00),326852.00000000)
R10=Circle((412747.00,958406.00),197166.00000000)
R2=Circle((672652.00,75788.00),902701.00000000)
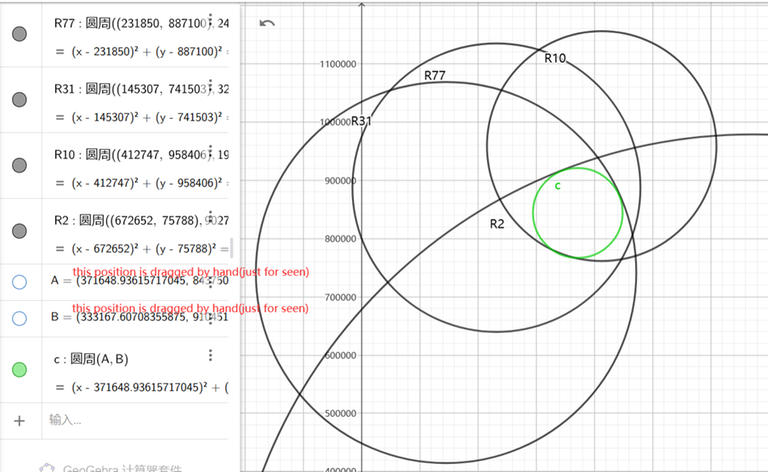
thus,our (R2,R31,R77) circle isn't restricted by R77,though we've known it should be restricted when we ends for-loop.that may become serious problems.when we use (R10,R31,R77) to instead (R2,R31,R77),R77 is still useless and the restrict of R2 is thrown away. When R2 is a useful restrict at R[1,77] the process will returned a invalid answer in spite of R2.
If you stick to let the result circle tangent to the three circle, instead of the biggest circle contained of the circles(like std is doing), there will be other questions like some input circle don't intersect with result circle(because it's not biggest).
The std solution returned NaN first time, when using my seed mt19937(321625) to call std::shuffle.Then it returned right, because it always reshuffle when returned NaN, but now no one can prove the correct of expect time complexity.And I don't know how to make that wrong or TLE.But the problem setter acknowledges that "There is a one-out-of-thousand chance that the returned answer will return a non-NaN value which deviates far from the actual answer." when testing his solution.
The data mentioned earlier can be downloaded from https://hydro.ac/file/4279/it.in .You can download it without login and have a test whether your solution is right when using seed mt19937(321625) and std::shuffle to shuffle the sequence.











Maybe you should ping the author chromate00 to check this.
I have consulted the coordinator for a way to fix this. If I can swap out the model solution to the $$$\mathcal{O}(n {\log_2}^2 n)$$$ tester solution that is guaranteed to work, then at least the problem becomes fine. I am unsure if this is possible however. I will keep you updated.