Господа, есть отсортированный вектор V из 10^7 элементов.
Например:
0 0 1 1 1 2 3 4 4 5 ...
Далее первый элемент вектора увеличивается на K, после чего вектор должен быть отсортирован.
Хотел бы узнать, какой из следующий методов является быстрее:
1)
V[0] += K;
sort(V.begin(), V.end());
2)
V[0] += K; i = 0;
while(A[i] > A[i + 1] && i < N - 1)
swap(A[i], A[i + 1]), i++;
3)
V[0] += K;
Через модифицированный бинарный поиск найти индекс **ind** куда можно вставить наш элемент
V.insert(ind, V[0]);
V.erase(V.begin());
4) Ваш вариант.
Буду благодарен.










1)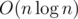 2) O(n) 3)
2) O(n) 3)  4) использовать список
4) использовать список
Спасибо, а как вы хотите со списком? можно пожалуйста пример?
Да ступил, список будет за O(n).
Можно multiset использовать, тогда удаление и вставка будет за
tmp = *mst.begin() + K;
mst.erase(mst.begin());
mst.insert (tmp);
так как мы увеличиваем только первый элемент, достаточно очереди с приоритетами:
спасибо большое, а вы не знаете как примерно реализован алгоритм вставки за O(long n) ? Просто сейчас нет возможности в исходниках копаться..
Обычно черно-красное (самобалансирующееся бинарное) дерево
Если все время нужно получать только самый большой элемент, лучше всего реализовывать двоичную кучу. Она же (скорее всего) реализована в priority_queue. Можете посмотреть ее реализацию вручную: 7099319, задча 446B - DZY любит модификации.