Manhattan Triangle

https://codeforces.net/contest/1979/problem/E

Given that the Manhattan distance between any two points is,

It's similar to adding two positive values whose sum is $$$d$$$. So, if we consider a point $$$(x,y)$$$ , then points that are at a distance $$$d$$$ from it are in the following form:

There could be more such sets of values if we consider adding $$$\pm d$$$ to $$$x$$$ or $$$y$$$.

If we look at the above set of points, all those points lie on a straight line with slopes $$$1$$$ and $$$-1$$$. This means considering a point $$$(x,y)$$$ , all the points that are at an equal Manhattan distance $$$d$$$ will form a square rotated by $$$45^\circ$$$ around it as a center.

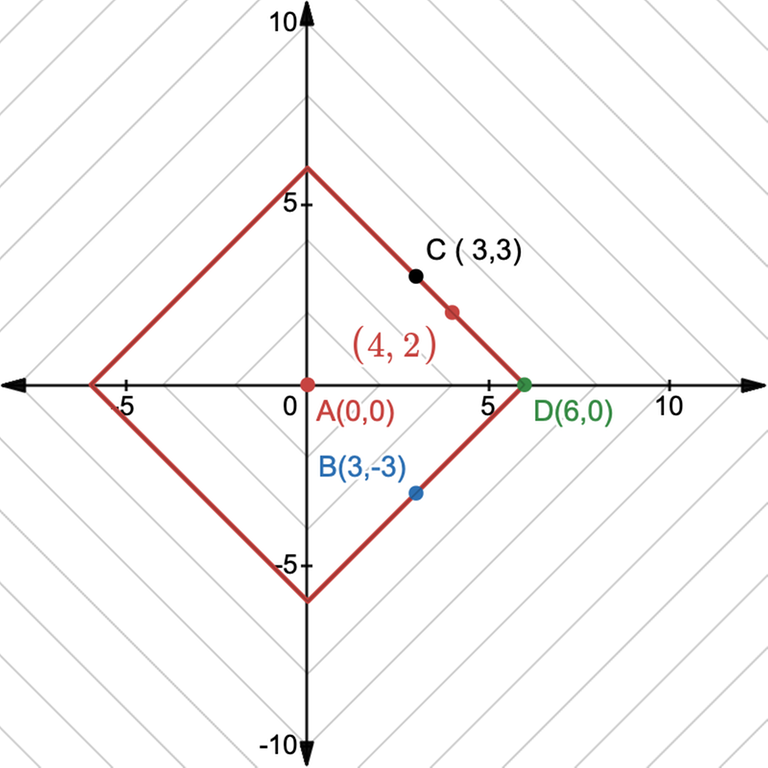
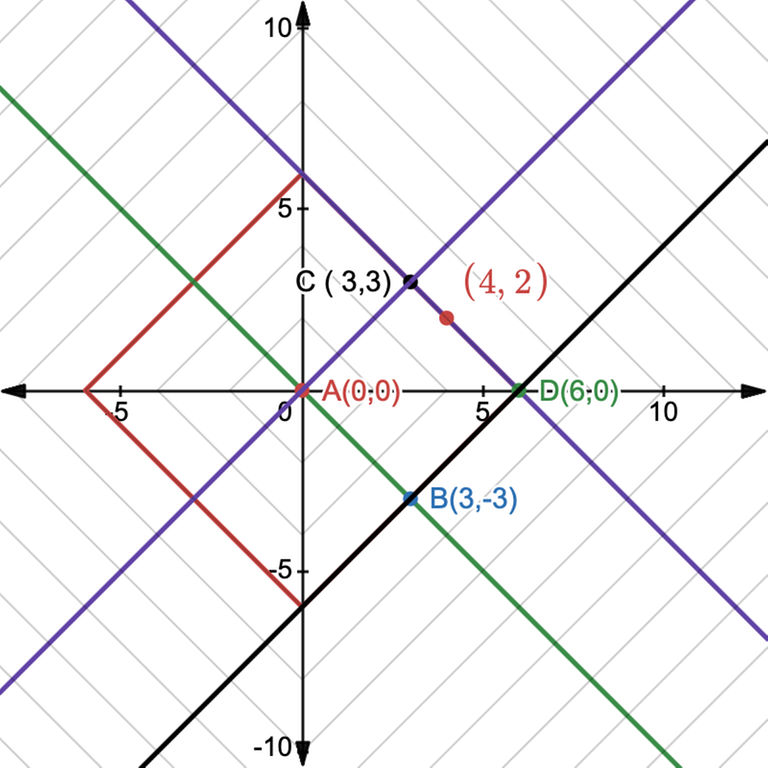
Let's analyze this square, ABCD.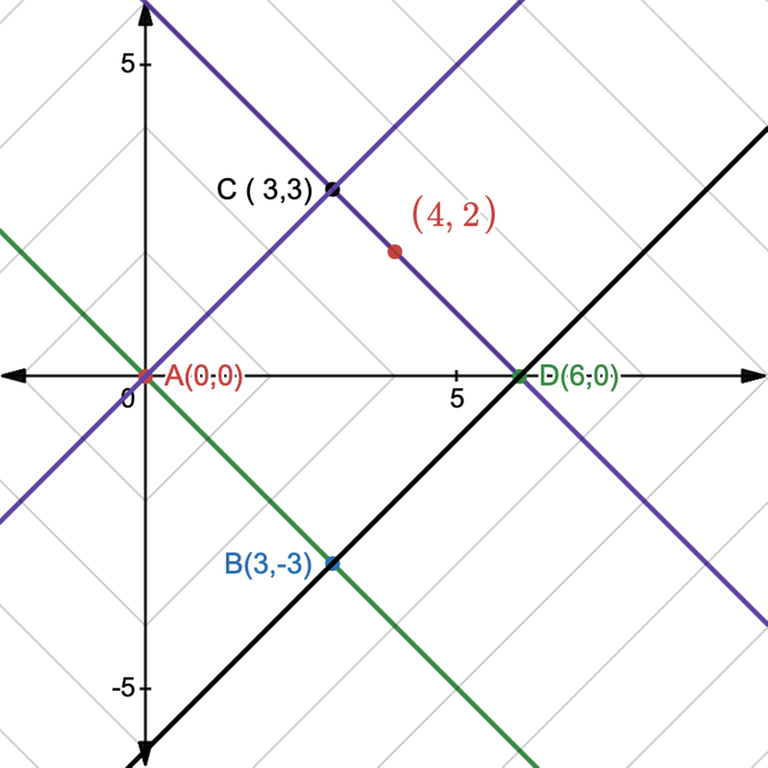

If we look at the square and select points A and B, then any point lying on the opposite side of the square CD will be at a Manhattan distance of $$$d$$$.

We will use this to solve the given problem.

If we transform the square by rotating it $$$45^\circ$$$ and scale it so that the sides become parallel to the axis, then all the vertical lines will reflect $$$x+y = d$$$ and all the horizontal lines will reflect $$$y-x = d$$$

Now, Lets consider

so each point can be represented as

Now, the line parallel to $$$X$$$ at a distance of $$$\pm d$$$ will be $$$X\pm d$$$, same goes with $$$Y$$$

Lets maintain three maps to represent the coordinates are their indexes,

type point struct {
    x,y int
}

X := map[int][]int{}
Y := map[int][]int{}
imap := map[point]int{}

$$$X[i] =$$$ list of all $$$Y_j$$$ lying on the line $$$X = i$$$
$$$Y[i] =$$$ list of all $$$X_j$$$ lying on the line $$$Y = i$$$
$$$imap[{x,y}] =$$$ index of point $$$(x,y)$$$

Transform all Points

for p:=1 ; p<=n; p++ {
            var pnt point
            fmt.Scan(&pnt.x, &pnt.y)
            temp := pnt.x
            pnt.x = pnt.x + pnt.y
            pnt.y = pnt.y - temp // y - x
            imap[pnt] = p
            X[pnt.x] = append(X[pnt.x], pnt.y) // x+y lines, vertical after rotation
            Y[pnt.y] = append(Y[pnt.y], pnt.x) // x-y, horz 
}

// sort to make the future search easier
for _,v := range X {sort.Ints(v)}
for _,v := range Y {sort.Ints(v)}

Check for Squares to select ABC

Lets start checking with left & right squares at the bottom formed with $$$Y-d$$$

For each point $$$(x,y)$$$ we need $$$(x,y-d)$$$ and a point between $$$[x+d, y , x+d,y-d]$$$

if _,there := imap[point{pnt.x, pnt.y - d}]; there {
                // check for C
                C_y := lower_bound(X[pnt.x+d], pnt.y-d)
                if (C_y != nil && *C_y <= pnt.y) {
                    fmt.Println(imap[point{pnt.x, pnt.y}], imap[point{pnt.x, pnt.y-d}],imap[point{pnt.x+d, *C_y}]) // A 
                    found = true
                    break 
                }

                C_y = lower_bound(X[pnt.x-d], pnt.y-d)
                if (C_y != nil && *C_y <= pnt.y) {
                    fmt.Println(imap[point{pnt.x, pnt.y}], imap[point{pnt.x, pnt.y-d}],imap[point{pnt.x-d, *C_y}]) // A 
                    found = true; break;
                }
           }

We should also check for squares to the top i.e $$$Y+d$$$

if _,there := imap[point{pnt.x - d, pnt.y}]; there {
                // check for C
                C_x := lower_bound(Y[pnt.y+d], pnt.x-d)
                if (C_x != nil && *C_x <= pnt.x) {
                    fmt.Println(imap[point{pnt.x, pnt.y}], imap[point{pnt.x-d, pnt.y}],imap[point{*C_x, pnt.y+d}])
                    found = true; break;
                }
                C_x = lower_bound(Y[pnt.y-d], pnt.x-d)
                if (C_x != nil && *C_x <= pnt.x) {
                    fmt.Println(imap[point{pnt.x, pnt.y}], imap[point{pnt.x-d, pnt.y}],imap[point{*C_x, pnt.y-d}])
                    found = true; break;
                }
           }

And, We are done!!