Добрый день. Возник вопрос: можно ли узнать номер перестановки (если их все выписать в лексикографическом порядке) за O(N)?
Заранее спасибо.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Добрый день. Возник вопрос: можно ли узнать номер перестановки (если их все выписать в лексикографическом порядке) за O(N)?
Заранее спасибо.
| Название |
|---|



neerc.ifmo.ru/wiki/index.php?title=Получение_номера_об_объекту_и_объекта_по_номеру
Я спрашивал о существовании решения за O(N).
Для маленьких N можно предподсчитать табличку размера 2N и дальше находить номер за O(N) на запрос.
Для больших N сам номер будет занимать порядка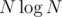 битов, поэтому его гарантированно не найти за O(N).
битов, поэтому его гарантированно не найти за O(N).
Спасибо большое, согласен.
Поясните, пожалуйста, как предпросчитать табличку? N <= 10 (думаю то, что надо)
Я умею табличку 2N·N:
2N даёт маска уже использованных чисел,
N — для какого числа мы хотим узнать позицию.
Поясните, пожалуйста, подробнее.
Все, сам додумал до конца. Спасибо.
(Нынче даже массив не очень нужен, операция popcount стала быстрой.)
Сначала решение за O(N2). Заведём булевский массив размера N: какие числа мы ещё не видели. Увидев очередной элемент перестановки x, мы хотим прибавить к номеру соответствующий факториал, умноженный на количество ещё не виденных чисел, меньших x. Например, для перестановки
4 1 3 5 2, увидев4, мы прибавляем 3·4!: ведь мы ещё не видели числа1,2и3, которые меньше, чем4. Дальше мы видим1и прибавляем 0·3!. Дальше идёт3, а к ответу прибавляется 1·2!: ведь из чисел, меньших3, мы ещё не видели только одно число2. И так далее.Теперь решение с битовым сжатием. Вместо булевского массива будем рассматривать двоичное число, например, типа
int. Бывшие элементы булевского массива превращаются в биты этого числа с соответствующими номерами. В остальном решение остаётся прежним.Ускорение: научимся находить, сколько битов с номерами, меньшими заданного, ещё не обнулены в нашем двоичном числе, за O(1). Тогда весь поиск номера будет работать за O(N). Увидев очередное число x, мы берём наши биты, оставляем только первые x - 1 из них (это просто
b -> b AND (2^x - 1)) и считаем количество единичных битов.Например, это можно сделать, посчитав для каждого возможного двоичного числа от 0 до 2N, сколько в нём единичных битов, и сохранив в массиве размера 2N.
В современных процессорах есть инструкция
POPCNT, которая делает это без предподсчитанных массивов за O(1).Круто. :)
a how does the code write? c++ sorry my isn't well
Here is an example: ideone.com/0E74XW.
thanks