I hope this post will be helpful for someone :).
I use a lot standard c++ gcd function (__gcd(x, y)).
But today, I learnt that on some compiler __gcd(0, 0) gives exception. (Maybe because 0 is divisible by any number?! )
Note for myself and everybody: While using __gcd we must carefully handle (0, 0) case or write own gcd.
upd: riadwaw noted below that we must be careful also with case __gcd(x, 0).











Good to know, thanks.
Why not use this for computing gcd ?
This work on Euclid algorithm. It is much faster then __gcd function.
but shorter to write __gcd(a, b), right?
I know that time complexity of my function is O(log(min(a,b))) but often is faster then that. __gcd say this:
I test two c++ program:
2.
On this test cases : https://sites.google.com/site/lovroshr/Home/gcd.zip?attredirects=0&d=1
It seen to be a first code faster then second for 0.1 s.
Not sure what exactly you were measuring, but I'm pretty much sure that the 0.1s of difference comes from a different place. Try to experiment with this and you'll see that your implementation is slower. For example, you can try to modify it and run on 10^6 random test cases and then compare the resutls.
@lavro-sindi, your code:
int gcd(int a,int b){return b?gcd(b,a%b):a;}
I have never tested it, but this realization is recursive, which may be slow. I use this, because it is fun and easy to code:
Before reading your comment I used to think that my implementation is a little scary:
But you definitely beat it:)
It's a perversion :).
Ordinary
while(b) a %= b, swap(a, b);is shorter (and faster on modern computers).Actually I tested some gcd implementations and here are results:
Source
First run:
Second run:
inline for recursive function? I think it's not correct, is it?
Why not? First, an
inlinekeyword doesn't force the compiler to inline the function, but only advises to do so. Second, for a recursive function it's possible to inline several levels of recursion and then actually perform a recursive call (just like loop unrolling). In MSVC it's even possible to directly control the level of inlining.Tail recursion can be eliminated and fully inlined. GCD falls into this category.
Thanks, I've understood)
Sorry, but gcd1 is so fast only because it's wrong.
To proove it, let's see, what variables will be equal to after each iteration, if a > 0 and b > 0.
The fastest implementation I've got is faster than built-in, but only a little:
I think this is faster since we dont have to use temporary variable
cI'm using this implementation
It works just like version with
whilebecause ofinline(I've tested it). Maybe your code is funny but my is easier to read ;-)Sorry about a little irrelevant question. I wrote some function with inline and it is slower than the same function without inline. I don't know when inline was better.
This is my function:
Using inline in this case make this function becomes slower.
Following the C++ FAQ the keyword inline is a black box. You don't know, will inline function work faster or slower.
I have best results with inlining recursive functions like GCD or DFS. Of course performance increasing is rather small, not more than 20% I guess.
This is undefined behavior.
Agreed. Upvote parent. Downvote and don't use grandparent's (izban's) version -- his version of the xor swap is not valid C/C++ code.
Why is it invalid?
In C/C++ there is the concept of sequence points, and you as the programmer must make sure that you (among other things) don't attempt to modify the same variable twice between two sequence points.
More reading: http://c-faq.com/expr/index.html (esp. item 3.3b) http://stackoverflow.com/questions/4176328/undefined-behavior-and-sequence-points
Very interesting, thank you. I have been writing such code for ~5 years, and I didn't know, that is is UB. Perhaps, you have saved me from a fail on some official competition :)
Can you explain this or provide a source for the explanation?
If you will just look at your xor operations and remember that a^a=0, then you'll know that all this xor is just next function:
it is easier to code, so...
I think your code is wrong. You should write swap(a, b) instead of a = b
Yeah, thanks. I fixed it now.
Is Euclidean algorithm faster than __gcd(a,b)?
if u're looking for faster code, i think this'll come in handy too:
it's all arithmetic and binary operations.
Which is UB anyway
yeah, u're right. although i've been using it for 4-5 years and it never behave abnormally!
__gcd(_EuclideanRingElement __m, _EuclideanRingElement n) { while (n != 0) { _EuclideanRingElement __t = __m % __n; __m = __n; __n = __t; } return __m; } why? __gcd use Euclid algorithm too
Again: it's not standard, but gcc-specific.
Well, in headers I see that on my computer it's defined in the following way:
So even __gcd(x, 0) won't work
thank you riadwaw.
By the way, is this bug? Maybe gcd(0, 0) = undefined, but gcd(x, 0) must be defined.
the mathematical definition is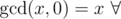 integers
integers  (including
(including 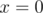 ).
).
By the way I heard that if we compute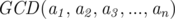 using the Euclid algorithm for N times, it will be not
using the Euclid algorithm for N times, it will be not 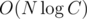 but
but 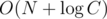 . Can anybody say something about it?
. Can anybody say something about it?
Seems true. Since we can take
C = min(a, b) + 1.It is easy to prove in the same way as asymptotic of Euclid algorithm is proven.
You probably know how asymptotic of Euclid algorithm for 2 numbers is proven. Suppose worst possible case. Take a look at pair (a,b), where a<b. It was received from (b,a+b). This one was received from (a+2*b,a+b). Previous one was (2*a+3*b,a+2*b)... You know from the proof, that Fibonacci numbers are actually worst possible case, and it takes log(C) to count GCD of 2 Fibonacci numbers less than C, and also to count GCD of any 2 numbers less then C.
Now if you have more than 2 numbers — let's do all the same moves in reverse order. If you have a pair (a,a+c), and currently working with number on position X, you should move to (a+c,2*a+c), like in Euclid algorithm with 2 numbers. Then you have a choise — you could either say "ok, 2*a+c was number on position X in input", and move to X-1, receiving pair (0,a+c), or say "a+c was number on position X in input" (then you'll move to X-1, receiving pair (0,2*a+c)), or you may keep going with this pair. It is clear that choosing 2*a+c for position X is worse, because choosing a+c gives you pair with larger numbers:) If you will decide to move from X to X-1 with 2*a+c, then in 3 moves (a+c,2*a+c)->(0,a+c)->(a+c,a+c)->(a+c,2*a+2*c) you will get pair (a+c,2*a+2*c). This pair is not better than (a+c,2*a+c), because c>0. And you made just 2 additional moves.
As far as you can do only O(N) moves "decrease X", and every such move gives you only 2 additional steps of Euclid algorithm, this proves your claim.
Or by the (perhaps faster) argument that the bigger number always becomes smaller than the smaller number after one iteration of gcd, and for further iterations of gcd the bigger number becomes at most half of its previous value (it’s not hard to see why).
So $$$N + 2 * log(C)$$$ is an upper bound.
Lol, what do you expect to be gcd(0, 0)? It is not well defined, so it should give exception. But fact that gcd(x, 0) is not working is indeed a shame :P.
Well, I expect it to be defined to 0 because it's the only value that will not break equalities
and (less importantly)
It's as defining a^0, first of all we define a^n and then say "Well, it could not be anything but 1 and it seems to work well". Or same with sum/product of empty list.
Let me disagree. It's definitely not like defining empty sums or empty products. In those equalities you wrote, once you have 0 somewhere in gcd computations you keep obtaining, so all calculation from that point are useless. Empty sums and products are very useful and are a good start to make useful computations.
First equality will still hold if we assume that gcd(0, 0) = undefined and demand of holding second equality in case of a=0 is like demand of dividing by 0 (or like demand that 5 * 0 / 0 = 5).
Frankly saying — useless discussion :P.
Well, I like useless discussions :D
But I don't agree first equation will not hold if gcd(0,0) undefined.
Consider case gcd(0,0,5) = 5, not undefined:)
BTW I do agree that some expectation make break smth if we define them to expected value (like 5*0/0=5) bit I don't anything that gcd(0,0)=0 will break
Oh, you're right with first equation :).
Actually gcd could be interpered as intersection (or sum, in euclid rings it is the same) of ideals generating by one element. In this case it is obvious that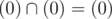
No it can't, the intersection of two ideals creates the lcm and not the gcd (else we would have a big problem since primes are equivalent to maximal ideals), gcd is the ideal generated by the union of the other two ideals. Your point that it becomes zero is still valid though.
Yes, intersection is lcm. Sum is gcd. Union is not ring at all
The ideal generated by a set is defined to be the smallest ideal containing said set, so yes the ideal generated by the union of two ideals is still an ideal.
I missed word generated. Then it is correct.
It is really useful being treated as neutral element in monoid of integer numbers respective to GCD operation.
You can use it when you calculate cumulative GCD's of several numbers: you can set initial value to 0 and then iterate in usual way making
val = gcd(val, A[i]). Any good GCD implementation will work with this pattern.It's also easier to write GCD segment tree using this property.
OK, you convinced me guys :).
you Can use
Hey, I want to bring this topic once again. I included this line:
in one of my code and ran it locally and in custom invocation on CF and it went successfully in both cases, but this comment: http://codeforces.net/blog/entry/13410#comment-182865 clearly proves that it shouldn't. So, what is going on? When can we use __gcd safely, when can't we? It depends on specific compiler and we should know which compilers provide safe implementation and which don't, am I right?
I looked into headers of g++ on my computer (versions 4.8.3 and 4.9.2). This is how __gcd implemented there:
I'm not sure if it was always implemented this way or it was fixed recently in gcc.
So it means GNU C++'s
__gcdwill work with (0, 0) (returning 0) and (x, 0) (returning x, regardless of given (0, x) or (x, 0))Right.
Moreover, if you look into the GNU GCC sources, it was always written this way in libstdc++ and the reason it was added is to be used internally in the implementation of std::rotate algorithm. But it seems the algorithm was rewritten in 2009 and this function is not used internally anymore. Since it's an internal function it may happen that GCC devs will just remove it on the next code cleanup, if they don't have some other reasons to keep it.
Regarding the riadwaw's comment, turns out it's the implementation from LLVM's libc++ and there it is also used internally to implement std::rotate algorithm, but they do all the necessary checks to ensure that (__x != 0 && __y != 0) before calling the function.
I think, it's one of the shortest and fastest implementations https://pastebin.com/FAe7dfRC
It's wrong implementation. It will fail when b = 0. Fixing it is easy, though the code will not look cool anymore.
it is the binary-gcd code that is very fast: binary-gcd code
A bit unrelated but I just wonder where you got it and if there are any more of such special functions in C/C++. I am just a newbie, thus I love learning more. Thank you.
It comes from practice.
While I was solving a problem, I discovered this bug.
By Special function, what you mean?
Is it special functions of C/C++ that you can use?
Click
or C++ related bugs and special cases?
Click
Click
Click
Click
I hope this will help you, a few links on my mind.
Hi, my Microsoft Visual Studio thinks that __gcd is undefined... Any solutions to that?
can __gcd(x,y) we use with x, y are long long ?
You may check it by yourself , no?
What is the time complexity of __gcd(x,y). Does it work on euclid's theoram?????
yes
In C++17 you can simply use
std::gcd(x, y)orstd::lcm(x, y).Maybe
__gcdis not a standard function?However,
std::gcdis a standard function in C++17.I use this function and it faster than __gcd(a,b); long long gcd(ll a, ll b){ if(a<b){a^=b;b^=a;a^=b;}return b?gcd(b,a%b):a; }
It has UB and it was already mentioned above. Please read comments before necroposting.
int gcd(int a, int b) { if(b==0) return a; return (b,a%b); }
in the above function, when i put a=63, and b=42, it gives output 21. But when i put a=42, and b=63, it gives output 42. why? Is it mandatory to put larger value at variable a and smaller value at side b?
Because you should implement it like this:
int gcd(int a, int b) { if(b==0) return a; return gcd(b,a%b); }. I don't know what does your initial code do.