Hello guys, I'm looking for some algorithm with complexity O(N) to find the largest continuous sub-array of an array V of size N, with sum equal to S. I know there are algorithms with complexity O(NlogN), but I don't know if it's possible with complexity O(N).
Can someone help me?










We can do this with a hashmap. First, let a_i be the array, and p_i be the prefix sums (i.e. p_i = a_1 + a_2 + ... + a_i). We can compute these prefix sums in O(N) time. Then, for each i, we want to find the smallest j such that p_i — p_j = S. We can use a hashmap to answer this query in constant time. We need p_i = p_j + S, so, as we are iterating through the prefix sums, add into the hashmap an entry with key p_i+S to value i.
Here's some pseudocode to help
ur solution is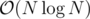 , not
, not  .
.
hashmap.containsKey could take O(nlogn) time, How would your solution be then O(n) ?
What about two pointers?
UPD: Well, it will work only if all numbers are non-negative.
You can use this algorithm:
scanf("%d", &n); ans = -100000000; for (int i=1; i<=n; i++) { scanf("%d", &a[i]); ans = max (ans, a[i]); } t = 0; for (int i=1; i<=n; i++) { t += a[i]; if (t>=0) { ans = max(ans, t); } else t = 0; } cout << ans;That's Kadane algorithm, for maximum subarray problem. Not for largest subarray with sum S!
I knew that but it is too late :v
Use a deque and have a variable to keep track of the sum of elements in the deck
insert elements to the back of the deque and add them to the current sum as long as (current sum < S)
As soon as current sum >= S check if current sum = S. If it is, the deque size is the size of a continuous sub-array with sum equal to S. now keep removing elements from the front of the deque till the current sum is < S then continue on
EDIT: while removing elements from the front of the deque you should check if current sum = S everytime
that works only for input with possitive values.
Lewin's post explains how to solve this problem.
So let's try to solve another problem: find the longest subsequence (not necessarily continuous) with sum S. I don't know fast solution. My only idea is to use polynomials: if we take polynomial (1 + xA[0])(1 + xA[1])... (1 + xA[n - 1]), then coefficient beside xS is a number of subsequences with sum equal to S. But if we modify it a bit, then we can get more information. So we bring in a new variable y. Now the polynomial (1 + xA[0]y)(1 + xA[1]y)... (1 + xA[n - 1]y) is very nice, because coefficient beside xSyk is a number of subsequences with sum equal to S and length equal to k. So we can use some fancy multidimenstional FFT and stuff to get the answer in something like O(Slog2S).
Does anyone know how to solve it better?