Thank you for participating!
2024A - Profitable Interest Rate was authored and prepared by Helen Andreeva with Artyom123
2024B - Buying Lemonade was authored by Endagorion and prepared by sevlll777
2023A - Concatenation of Arrays was authored and prepared by Mangooste
2023B - Skipping was authored and prepared by adepteXiao
2023C - C+K+S was authored and prepared by yunetive29
2023D - Many Games was authored and prepared by Tikhon228
2023E - Tree of Life idea by isaf27, solution and preparation by Ormlis
2023F - Hills and Pits was authored and prepared by glebustim with vaaven
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...










Ormlis when will hidden test case and source code of others be visible?
Only administrators can do this, not me.
Oh sorry I didn't know. Btw great contest Thank you
Hi, I cannot prove my solution for div1D nor hack it I hope someone can hack or prove it.
287108342
The idea behind my solution is to have $$$dp[\sum w]$$$ store the maximum probability that we can achieve.
As with the editorial, for a fixed $$$p$$$, we should only take a prefix of the weights (when we sort from biggest to smallest weights). So we will also store that information (in the code it is
signed dp[400005][100];, for statedp[x], we take the biggestdp[x][y]elements with p=y.When we transition, we will try for all y to do
dp[x][y]++.This doesn't seem right because it is possible for the optimal answer to be killed early when there is another state with a bigger probability for the same $$$\sum w$$$ but is worse at extending to larger $$$\sum w$$$
I guess Trial and Error rocks even at IG level lol.
My question is, isn't the maximum sum of weights supposed to be much bigger?
Refer to editorial above on why we can bound sum of weights by 200k
i swear i can't figure out for the life of me why my solution to B isn't correct, and i'm not allowed to look at the failing test case either.
I dont know about the formulas, but you should use long long instead of int.
thanks a lot, this was one of the two errors in my code, i just put * 1LL into the formula and it stopped overflowing. i never realized that the whole point of my formula was to keep running till we exceed k, and if k was 1e9 then it would overflow.
Bro your code won't return any output if k is equal to sum of all elements of the array.
Try
1
3 6
1 2 3
Comment if you want me to fix it
that wasn't actually the error, i ran this test case before submitting. the actual error was me decrementing n within the loop while having the loop run n times, so if n was 4, it became 2 after the loop ran twice and exited. apart from this i needed to use long long too.
thanks nonetheless! lesson learnt: always dry run code in a verbose manner :)
+almost always use long long. I had the same problem and spend about an hour before realizing it.yeah, i think it's probably best to develop the habit of using long long for now
Same, I'm new to Codeforces and have been giving contests, but the solution to be just wouldn't come to my mind, I wasn't able to understand the 2nd last test case at all.
then $$$c_p \cdot q^{c_p} > (c_p - 1) \cdot q^{c_p - 1}$$$; otherwise, the smallest element can definitely be removed.
why?
I also want to know "why?" Otherwise it's not a proof.
This way doesn't give me intuition, but I was able to derive what we need.
Suppose we have now sum $$$W$$$ and current probability $$$Q$$$, and we add item $$$w_i, q_i$$$. and we already had $$$c$$$ of those with probability $$$q_i$$$. Also denote $$$A = W - w_i \cdot c$$$. I don't know how to avoid this trick. But, in other words $$$W = A + w_i \cdot c$$$. Then we making worse if:
So, when count of same probability becomes larger than this, we only reduce value. Notice that when $$$c > \frac{q_i}{1-q_i}$$$ it also $$$c > \frac{q_i}{1-q_i} - \frac{A}{w_i}$$$, because both $$$A$$$ and $$$w_i$$$ are non-negative. So, when $$$c$$$ is greater than $$$\frac{q_i}{1 - q_i} = \frac{p_i}{100 - p_i}$$$ we won't gain any profit by adding more $$$w_i, p_i$$$ pair. Note, we assume we add $$$w_i$$$ in non-increasing order.
I did a similar claim, proves pretty much the same thing.
Suppose we took an optimal subset whose weights sum up to $$$S$$$, and let's fix some $$$(p, w)$$$ taken ($$$p<1$$$). Then optimality implies that the solution without this element, is not better. We can ignore the product of probabilities on both sides of the inequality and get:
$$$S - w \leq pS \to S \leq \frac{w}{1-p}$$$. If we took $$$k$$$ elements of probability $$$p$$$, with differing weights, then denote by $$$w$$$ their minimal weight. So $$$S \geq kw$$$, and $$$w$$$ can be plugged in the inequality above to get $$$k \leq \frac{1}{1-p}$$$.
The intuition behind the whole idea was easier for me to see in contest when I tried to bound the number of elements taken for $$$p = 0.5$$$, and certainly you won't take an element if it doesn't double your current sum.
thanks! it's very clear now
C is a piece of dogShit,i mean why it had to be based on some crap observation.It could have been improved by giving a formal proof of why does that always work. Disappointed...
What's wrong with the proof provided?
Another solution is to sort the arrays by comparing pairs $$$(min(a_{i,1}, a_{i,2}), max(a_{i,1},a_{i,2}))$$$. We can observe that if we move the array with minimal element to the left (and among these with the least maximum), the number of inversions cannot increase, so that's optimal order
lol yeah that was my method
I did the same but received WA: 286985983. I reverted the order of checking (first max and then min as opposed to first min and then max) and it got AC : 287000832. Still unable to understand why that happened.
A grave mistake in my first submission. I modeled <= comparison in the custom comparator of sort function instead of <. Basically, at the end of the custom comparator, I should have returned false instead of true. Correct submission: 287210506
It has more to do with your lambda and how the sorting is handled using std::sort. I don't know exactly why but I think I read somewhere that it is usually recommended to do a "stable sort" with std::sort, as such I simply changed the "true" to "false" when the arrays are same, which makes it a stable sort, and thus got AC, 287213481.
can you check my solution for div2 C . why it is giving me wrong answer 286973745 plz check it.
Even this works...
I solved this problem by just randomly trying different methods of sorting the arrays..
sort ascending by first then by second
or vice versa
or by min in pair .. etc
and then one of them by luck was successful
I didn't like the problem because I couldn't reason about it in any way but this shows that one can learn sth from this problem, like what is an exchange argument
Consider the simple case of only 2 pairs:
a b
c d
Note that we can't do anything for the inversions within the pair itself so we don't compare a with b or c with d
Now consider the case where b < c and a < d
We can concatenate the pairs like this ( a b c d ). This won't add any unnecessary inversions.
We can rewrite the inequality ( b < c and a < d ) to be ( a + b < c + d )
We want to ensure that this inequality is true max possible amount of times, Hence this can be achieved by sorting the pairs according to the sum of each pair.
Ormlis In D2C, how can we solve the problem for arrays of sizes three or more? I tried to solve it by comparing inversions of ab and ba for sorting but it seems this condition is not transitive and thus doesn't work for arrays of twos either, so I had to use some other min/max technique, which doesn't seem to generalise for sizes more than 2.
It will be quite more difficult because we can't use exchange argument anymore
Would you have any method for solving it?
For lists of size four or more, this problem is known to be NP-complete, as you can read in, for example, "A Note on the Complexity of One-Sided Crossing Minimization of Trees" by Alexander Dobler. For lists of size 3, this problem is conjectured but not proven to be NP-complete.
Would you be aware of any source where I can read about the conjecture for lists of size three? I couldn't find any articles or papers on this topic myself so I need a little a help, thanks!
The original proof is here though: https://link.springer.com/chapter/10.1007/3-540-45848-4_10
got IGM but still cannot solve A during contest, isn't weird?
A simpler solution for 1E:
When you choose a node as the root node, our answer is at least $$$\sum_{i=1}^n \frac12 s_i(s_i-1)$$$, where $$$s_i$$$ is the number of children of node $$$i$$$.
However, such a construction may not be able to satisfy some edges that pass through both the son and father at the same time. Let's consider the contribution of this situation to increasing the answer.
We set a dp state $$$f_i$$$ to represent the number of residual paths that can be uploaded through the parent when the node $$$i$$$ calculates the necessary contribution internally (i.e., the above equation).
Transfer as follows:
$$$f_u = \sum_{v\in son_u} \max(1 - [u\text{ is root}], f_v - (s_u - 1))$$$
After calculating $$$f_ {root}$$$, we must pair the extra paths pairwise, and when we choose the node with the highest degree as the root, we can prove that there must be a match to make the scheme valid:
[tbd, prove is hard]
So we can calculate $$$f_ {root}$$$ and add $$$\lceil\frac{f_{root}}2\rceil$$$ to the equation at the beginning.
using translator.
287001804
Is there a reason the submissions and testcases are still locked?
Just a FYI the source code was visible for few mins I think after the contest ended. I'm not sure was it intended or was it some kind of bug.
Samples on D1C are useless
B : can anyone tell me what is wrong with my solution , I can't figure it out, frustrated !
I used the same logic
I thouth Convex Hull Trick would work on 1D because they seems simular. But it didn't so I'm sad.
Here's my binary search approach for Div2 B:
I didn't understand D1C from the tutorial, can someone explain it in more detail
A bit late, but here. Consider a cycle of length k in one of the two graphs. Enumerate the vertices along the cycle as the official solution does. So the first vertex gets label 0, second 1, and so on to k-1 which is connected to label 0. Imagine that the cycle branches at the node labeled 5.
Because the graph is strongly connected if that edge is incident to vertex "e" then there must be a path from e to the node labeled 6 that does not use any edge more than once.
(why? we have used only 5->e and by definition there must be a path between any two vertices. Any path from e->...->6 that includes 5->e can be done without it because it must include e->6 after it (e->...->5->e->...->6)).
e->...->6 must have a length of a multiple of k because then we would have a cycle of length not a multiple of k.
(why? We can go from 5->6 in 1 move, or we can go from 5->e->6 in |e->...->6|+1 moves. We know we have a cycle of length k through 5->6 so |0->...->5| = 5 and |6->...->0| = k-5-1 so |0->...->5|+|5->e->...->6|+|6->0| = lk. then (5)+|5->e->...->6|+(k-5-1)=lk then |5->e->...->6|=(l-1)k+1)
So every path must conserve this coloring property and this is the only property required. (proof: collapse every node of the same color into a single node and conserve edges the only cycles remaining are of length k, longer cycles just represent going around this graph more than once).
Now we can just add edges from k -> k+1 as needed to solve the problem.
Thanks it helps
I feel so dumb. :( .
Why?
I had different solutions for both div2 C and D
for C it's a completely different one, I used the following sort
for D, Instead of building a graph I used a minimum segment tree to build the distance array so let's say we got d[i] = get(i,n), then we update seg(b[i],min(d[b[i]],d[i]+a[i]))
Yes, task D2D has a solution with a Segment Tree, some participants of the olympiad and rounds wrote it, but it seems to me that the solution with Dijkstra looks more concise :)
For Div2 C, I initially tried to sort any tuples by the following condition. Consider the two possible arrangements [tup1[0],tup1[1],tup2[0],tup2[1]],[tup2[0],tup2[1],tup1[0],tup1[1]] and in whichever arrangement the number of inversions is less I put that first. I got wrong answer on testcase 1123.I saw @Dominater069 also try to do the same initially. Can someone please explain why this solution is wrong?
I had done the same thing initially. I suggest you read the following if you are not aware of transitive conditions for sorting.
Exchange argument: Suppose there is a correct arrangement of the arrays. The editorial proposes a solution that says the arrangement created by sorting based on sum. We now only have to prove that any optimal arrangement can be transformed into the exact arrangement based on ascending sum, without worsening the answer.
Transitivity: Now the condition of sum is transitive, i.e. sum(a) < sum(b) and sum(b) < sum(c) means sum(a) < sum(c). Now, if the correct arrangement has a pair of indices which doesn't follow this sum order, then we can argue that there is at least one adjacent pair such that they are out of order. The proof is simple. Assume there are non-zero number of elements between the closest pair of out of order pair, hence all the elements in between them are individually in correct order with either of them. Pick a random element x in between them. a < x and also x < b, so it must be that a < b, but we just assumed a > b. Hence the closest pair cannot have correct order elements in between them.Now when we flip the order of the two adjacent arrays, their ordering doesn't matter to the rest of array, but only on the relative order of the two adjacent elements which we show can be flipped without worsening the solution. We can keep arguing and flipping adjacent pairs until there is no pair out of order. Hence we can transform the correct arrangement to our preferred arrangement without worsening the answer.
Since sorting by (min, max), (max, min) or sum are all transitive conditions, all of them have a similar exchange argument and are all correct.
TL; DR: The count of inverse for ab and ba is not transitive and it cannot be guaranteed that the optimal answer will have adjacent out of order pairs (ordering based on Inv(ab) < Inv(ba)), if they are not adjacent then swapping them affects all the elements in between and thus it cannot be guaranteed to not worsen the answer.
Such a nice explanation! I didn't actually think about how sorting works!. Thanks a lot. Here is a testcase for anyone else who will read this in future after having made the same mistake as me. [[3,3],[4,1],[2,2]]
silly question please forgive and answer : how exactly did we show that swapping the 2 adjacent out of order pair will not increase the inversion between them ? is it just be trying some cases ? it's clear that it will not affect the left or the right part of the array but what about the 2 pairs them self ?
yes it's casework only, and can be proven by brute forcing all possible cases. There is no general theorem regarding this, for example the order by summation heuristics becomes untrue for sizes starting from 3.
I feel like the test cases on D1C are quite weak because I just accepted it with a simple $$$O(K^2)$$$ brute force that checks if the two pairs of counting arrays are equal for any cyclic shift.
On the other hand, I assume it will be hard to generate such a test case if people construct the adjacency matrices and run DFSs differently because this will introduce some randomness in the resulting counting arrays, although that is not the case since most people just run DFS starting from vertex 1 (that is what I did in my accepted submission 287195742).
Was there an attempt to create some test cases against such an obvious brute force?
Uphacked. Also, I think it's not hard to prepare a few of such cases with different "shifting" of the node numbers so that these "lucky" codes cannot pass. Since its average number of iterations would be something like $$$\cfrac{K^2}{4}$$$, it's very unlikely for them to run in the TL even for like 2 of such cases.
anyone, can you find where will it fails.
isn't constant C in problem 1D just $$$200000 + 1$$$, not $$$200000 \times \left( \frac{100}{99} \right)$$$
UPD: I think my claim is wrong, but it gets AC with $$$C = 200000$$$
Use brute force with O(K^2) time complexity to check the cyclic shift in Div.1 C can be accepted. Can it be proved right or just there isn't any hack yet.
submission
Hacks to D1C have got
Unexpected verdict. Ormlis can you check the validator?link
Yes, sorry about this. It seems we didn't have good tests against cyclic shift checking in O(k^2), and you hacked one of the solutions, that was marked correct in polygon.
2023D - Many Games There is statement $$$W\cdot (100 - p_i) > 200000$$$. It's not a simple one.
Denote $$$L = 200000$$$. We said we assume sum of $$$w_i$$$ is greater than $$$C$$$. This means $$$W + w_i > C$$$. So we have:
To prove the claim, it's enough to show that
With constraints:
Idea is: for any fixed $$$C$$$ we will find minimum of $$$(C - w_i)\cdot(100-p_i)$$$. To do so, assume $$$C$$$ and $$$p_i$$$ are known, and find $$$w_i$$$ for which the function reach minimum. In this case $$$100-pi$$$ is just constant, so $$$w_i$$$ should be maximum. But we have constraint, thus $$$w_i = \frac{L}{p_i}$$$.
Next, assume $$$p_i$$$ is variable, and find the best value for $$$p_i$$$.
We want when $$$1 \leq x \leq 99$$$ because only in this case extremum point to lie within the range. Otherwise we only need to check $$$x = 1$$$ and $$$x = 99$$$ points. Because only them can be minimum.
Outside this range only probability 1 and 99 matters. Substitute $$$p_i = x$$$:
So, the value for this extremum point when $$$p_i$$$ satisfy constraints is:
For all $$$C$$$ we also need to check for $$$p_i = 1$$$: (we still use $$$w_i = \frac{L}{p_i}$$$)
And for all $$$C$$$ we also need to check for $$$p_i = 99$$$:
So, for given $$$L$$$, we need to have $$$C \geq L \cdot \frac{100}{99}$$$ to meet requirements above, and also since $$$L \cdot \frac{100}{99} \geq L \cdot \frac{100}{99^2}$$$ for cases when $$$C \leq 100\cdot L$$$ we need to make sure:
But $$$L \cdot \frac{100}{99} \geq \frac{L}{25}$$$, so we need only one requirement $$$C \geq L \cdot \frac{100}{99}$$$. For $$$L = 200000$$$ we get $$$C \geq 200000 \cdot \frac{100}{99}$$$.
A little note: extremum point happens to be the maximum. But I don't know how easy to show that it's maximum, so easier to show that it is never less than "endpoints" ($$$p_i = 1$$$ and $$$p_i = 99$$$).
About your analysis and your commentary about checking if something is minimum/maximum, you only need to check if $$$f"(x)$$$ is greater/lower then 0 at the points where $$$f'(x)$$$ equal $$$0$$$. This makes your analysis easier, as $$$f"(x)$$$ only assumes the sign required to be maximum overall $$$x > 0$$$. From this you only needs to compute $$$f(1)$$$ and $$$f(99)$$$ to check the inequality, removing the need to verify points with $$$f'(x)$$$ equal $$$0$$$ for $$$x > 0$$$.
In 2023B Skipping tutorial above, can anyone help me explain why we are allowed to do this "Now we are allowed to visit each problem as many times as we want"?
It's because we defined the subproblem as we can move on to each problem, no matter if we already solved them or not.
Thanks for your answer. But could you let me know why " no matter if we already solved them or not." In the problem description, we can not visit the problem which was previously submitted or skipped
What you are mentioning is the constraint on the main problem, while this sentence is based on the subproblem that we just newly defined. We first solve the subproblem without the constraint, and then verify that the subproblem indeed solves the original problem.
Once we solve the subproblem where we can visit the same vertex multiple times using shortest distance algorithms, we also know that it guarantees that each vertex is visited at most once (because visiting a vertex multiple times never helps with improving the shortest distance), so we see that it indeed does not matter if we're trying to visit the same vertex multiple times or not. Therefore, going back to the main problem, if we reach to a certain problem $$$i$$$ with the least penalty possible, we can then solve all unvisited problems with index $$$\le i$$$, receiving the prefix sum of the scores minus the penalty as the total score.
I got it. Thank you so much
How do you generate such graphs for problem div1C ,or do you just originate all cyles from the same node.
Can someone pls tell why i got runtime error in pretest 4 for Div2 C , i sorted the array based on sum of elements
https://codeforces.net/contest/2024/submission/286970228
It's the same issue as https://codeforces.net/blog/entry/135370?#comment-1210592
thank you , also found this https://codeforces.net/blog/entry/70237# , hope to remember this next time
My approach to D2C was sorting the array by the smallest element in the tuple. I was wondering if this is an actual solution to the problem, or if the test cases were simply too weak?
What's the necessary proof for D1C? Like if there doesn't exist a cyclic shift so the frequencies are the same, then there's no solution? I think the editorial only shows sufficiency.
Can anyone please explain me the intuition behind Div2C, I am unable to derive the intuition. I saw a tutorial and it just said to think of max-min of pairs. But how and why did we arrive to this max-min of pairs?
how would you do the concatenation of arrays question if there were 3 numbers in each array?
.
We can solve D problem (Many Games) faster. My optimization: for each element with p probability and w winning sum we can only choose winnings which sum we can improve.
Formula: x < p*(x + w) => x * (1 — p) < p*w => x < p*w/(1-p). x is the sum of set to which we can add our element.
Problem — Buying Lemonade
In test case 2 I am getting this error "wrong answer 958th numbers differ — expected: '8', found: '7'". Since large test case gets truncated, how do I debug this?
Submission
In C, why the arrays can't be sorted in order of the number of inversions of two adjacent arrays. Just like this:
Is there any counterexamples?
https://codeforces.net/blog/entry/135341#comment-1210479
Hello guys, I'm new at Codeforces, and I was curious about Problem B. My solution's logic is sorting the array in increasing order and then choosing the lowest element. After that I had to multiply it by n (which is the same as if I pressed every button at least once). If it wasn't enough, I add that and other numbers with the same value to the variable "count" and move on to the other value. What's wrong with this solution?
296495727
here is an optimal arrangement for minimal inversion count in the div2C- 2023A - Concatenation of Arrays:
testcase: data = [(12, 14), (6, 2), (10, 4), (12, 11), (5, 8)]
optimal arrangement: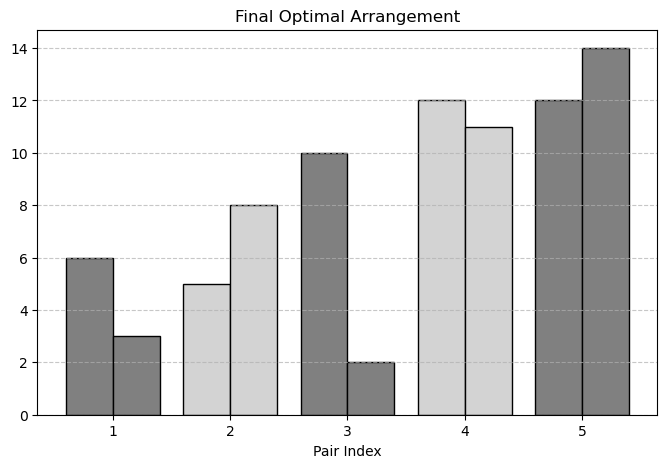
data = [(6, 2), (5, 8), (10, 4), (12, 11), (12, 14)]
why this works?
notice that disturbing the position of any pair would increase the inversion count. lets verify this. lets shift the pair (10,4) from index.3 to starting position. notice that the increment of inversion count caused by the number '4' in the optimal position is lesser than the impact caused by the number '10' after rearrangement.
the red color numbers are those numbers whose inversion count is incremented due to the currently affecting number (in yellow color)
conclusion: the position of the pair in optimal arrangement may increment inversion count only fewer elements on its left, but placing it anywhere else would guarantee the increment of inversion count of all the pairs.
this seems to be a mare observation, i initially thought this question would be way tougher.