Hello everybody,
About an year ago I participated in a competition and I did pretty badly and I didn't look at the problems for a while. Recently I tried to solve them and solved one of them, but the other, I just couldn't solve. I've tried for a while but can't come up with anything good enough, so I'd love some help. Here is the shortened statement:
You are given a square of size N (1<=N<=20,000) and a list of M (0<=M<=200,000) cells that are dark, all other cells are bright. The problem is to calculate the sum of all areas of rectangles that are of the same color. That is, output the sum of all rectangles in the initial square grid that are fully dark or fully bright.
Print the answer modulo 10^9+7, since it can be very large.
Input format : N and M on one line, followed by M lines describing the coordinates of the dark cells 1-based.
Sample input:
4 6
1 2
1 3
2 1
2 3
4 1
4 4
Sample output:
58
There are 6 dark rectangles 1x1 and 2 dark rectangles 1x2 and in total area of 10 of dark rectangles. The total are of bright rectangles is 48, so in total 58.
I'm struggling to find any good solution, the format of the competition is to give output files for the given input files, so I suppose something like O(N*N) or maybe even O(N*M) could be the intended solution.
Thanks in advance!
Hah, Marathon24, which I prepared :)).
Have you ever heard about that problem: http://main.edu.pl/en/archive/oi/9/dzi ? In Poland that is a very well-known problem and we are referring to many problems as some modification of "Działka". But even though, main idea should be well-known not in Poland only.
My solution was different than author's (monsoon) solution, so there are at least 2 essentialy different solution, though both of them are "Działka" modifications.
By the way, if M is small that problem can be solved by inclusion-exclusion principle even for very big N.
Marathon24 will be held also this year and registration started yesterday, I encourage you to participate :)! This year you can also encounter some problems prepared by me, but that year I'm preparing 2 problems only (year ago that was more or less everything :P) and they are not authored by me.
Yes, I already registered that's why I was asking, since I looked at last year's edition to check why did I do so badly. However seeing how many teams registered on the very first day and adding that I'm not really good at marathonic-type problems, my chances of qualifying are really low :D
I'm sure you'll have some interesting problems, hope I solve them!
And thank you for the answer :)
Note : I think I've seen the problem you've linked but I can't see how to use it here, could you hint me?
Edit : I'm not sure if I can even solve that "Dzialka" problem, is there some editorial on it? I'm not familiar with that website.
This problem I linked is not supposed to be exactly applied in this problem, I meant that general idea is the same. It's kinda hard to describe without any pictures. Firstly for every fixed cell you determine how many good cells you have directly above your cell (you stop counting when you encounter black cell or a side of board) — trivial DP. Then, for any fixed row, in each cell you got "tower" of good cells of computed height. You process that row from left to right and in each moment you should keep stack of informations like (x_i, h_i), which mean "on interval [xi, xi + 1) all heights are at most hi" and sequence h should be nondecreasing and for each x corresponding h should be as large as possible, it is something like "suffix minimum".
In other words, when processing that fixed row, for each index j you should have determined values suf_min[i], such that sufmin[i] = min(h[i], h[i + 1], ..., h[j]), where h[k] is height of $k-$th tower in actually processed row. In order to update that infos quickly you need to store them as stack of intervals of equal values. With that kind of informations you should solve Działka problem and modifying it you should solve Marathon problem.
I'm trying hard to understand this now, since it looks like a really useful technique.
Now if for every j we can get suf_min[i]=min(h[i],h[i+1],...,h[j]), then wouldn't that be simply a kind of static RMQ, or am I missing something.
If you have some time could you show me how the stack looks for h={4,2,3,4,1} ?
This stack is changing in time. We do something for every row and that formula for suf_min was for fixed row and fixed moment in time in processing it (exactly after considering first j cells from that row).
Firstly let's look how array of suffixes minimum changes in time:
4
2, 2
2, 2, 3
2, 2, 3, 4
1, 1, 1, 1, 1
Then, stacks look like this:
(1, 4)
(1, 2)
(1, 2), (3, 3)
(1, 2), (3, 3), (4, 3)
(1, 1)
P.S. Does anyone know, how to break line without actually breaking 2 lines :d? This looks somehow ugly xd.
Thanks Xellos!
Oh, I got it! I think I know the solution of "Dzialka" now, and I'll try to code it. Thank you very much!
P.S. I think the only way to fix double new lines is to add them in a code block (as I did with my sample input and output exactly because of this reason), ugly indeed :D
P.S.S. My solution got quite slow since my implementation wasn't the best, but produced all the correct outputs on the marathon24 problem, so thank you very much! :)
<br></br>tags should worksomething
something else
I'll try.
Since M is small enough, we could try to do something with it. For example, sort the dark points and for point i, count the sum of areas of all rectangles that contain point i and none of points i + 1... M - 1.
Suppose we fixed the i-th point (x, y) and the bottom side d of our rectangle. We must exclude the nearest black points that are in rows x + 1... d from the left and in rows x... d from the right, which gives us bounds on the left and right sides (lm, rm) of the rectangle. These values can be precomputed or 2-pointered or whatever, in O(N2) time total. We have no bound on the top side u other than u ≤ x (and of course l ≤ y, r ≥ y) and it's clear that any such rectangle is valid.
The sum of areas of all such rectangles should be
Now, the trick is why this isn't $O(NM)$. We can only move d down until we reach the next dark cell in column y. This way, we'll only visit each cell once as (d, y) — for the first dark cell that's above it, and so this works in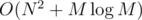
.
Wow, that's actually very clever solution, thank you :)
I'd have some trouble working out the formula but the idea is quite simple and I like that!
Note: Using your way I can only calculate the sum of areas of the bright rectangles, I might be missing something, but how do you calculate the sum of areas of dark rectangles?
Switch white and dark cells. Then M changes to N2 - M, but it is only O(N2) to O(N2logN) change.
Actually, we can sort in O(N2) (it's just that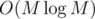
gives a better runtime for the original constraints), so it's still O(N2) :D
Is there somewhere I can read about sums and the basic properties of how to work them out to get a formula? I'm 16 and haven't studied that in school so I'm having difficulties understanding how you derived that formula, and it looks like a powerful thing to know :)
To derive this thing, you just need to know the formulas for area of a square and sum of arithmetic progression... and have a lot of practice with ugly/long expressions. When you can solve part A of this problem without mistakes, you're a sage in that regard :D
(there's a story going about one Czech contestant who didn't even try solving it during the competition; instead, he wrote an essay about why that problem is incredibly ugly and disgusting)
Haha, well, I agree with that contestant :D
And well, I guess I'll copy your equations and try to understand them slowly on paper, thanks for answering my questions :)
Oh, thank you, I feel kinda stupid now, don't know why I felt like sorting N^2-M points would be too slow!