A few days ago, the UKIEPC 2024 was published, and I became interested in the problem Hedge Topiary. After several attempts, I got AC, but I knew that my solution should fail in some cases, so I set out to break it. Unexpectedly, I also broke the official solution. After analyzing it, I come to explain why it doesn't work. Later, I will explain my idea (which I hope is robust enough). This post is intended to be more educational than anything else. Also, I apologize if I am not clear enough and if I have some mistakes in English.
Hedge Topiary
Official site with the package (code) and slides
Official idea

In summary, we can say that the official solution tries to obtain the ranges where the vertices of A are completely contained in B by verifying that the points of A (on the perimeter) that lie on the rays from the origin to any vertex of B are also contained. I understand that the idea arises from the fact that the intersection of two sides always starts and ends at a point. However, this idea has a major problem: the fact that those points are completely contained does not imply that the entire segment is contained (referring to those that share a vertex with the point being analyzed).
Below is the test case that broke this idea.
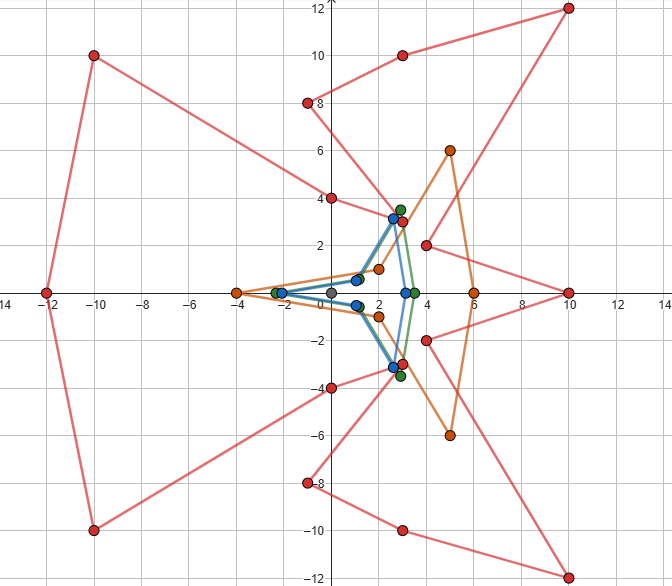
The red polygon is polygon B (static), the orange polygon is polygon A (the one that needs to be scaled), the green polygon has the scale obtained from the official solution, and the blue polygon is the correct answer.
Let's take a closer look at the scales.
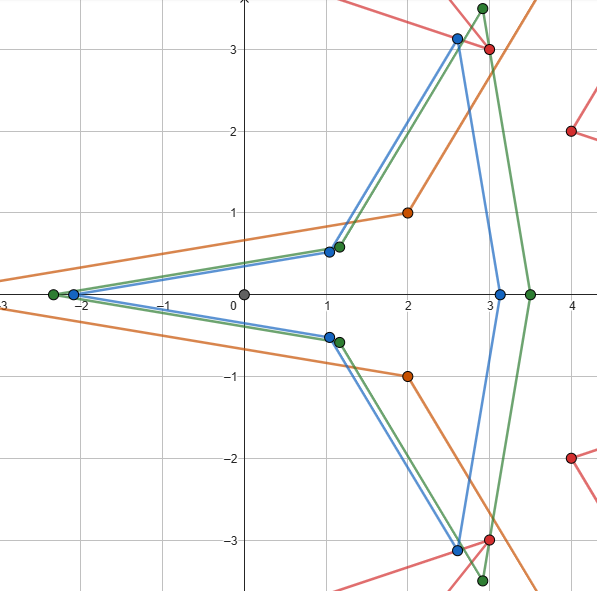
We observe that all the vertices of A and the points on the rays from the origin to any vertex of B are completely contained, but not all the segments.
My approach
We will calculate the intervals where a segment of A is intersected by a segment of B. This allows us to ensure that within those intervals, the answer cannot be located. Furthermore, since both polygons contain the origin, it is not possible for A to go from being completely outside of B to being completely contained within B. We will obtain a set of intervals between the intersections where our answer might be located. Next, we will see how to construct the intersection intervals and, subsequently, how to construct the answer.
First, we can have two types of segments of A with respect to the origin (Collinear or not).

We will first analyze the case on the right and the scenarios in which it can intersect with a segment of B.
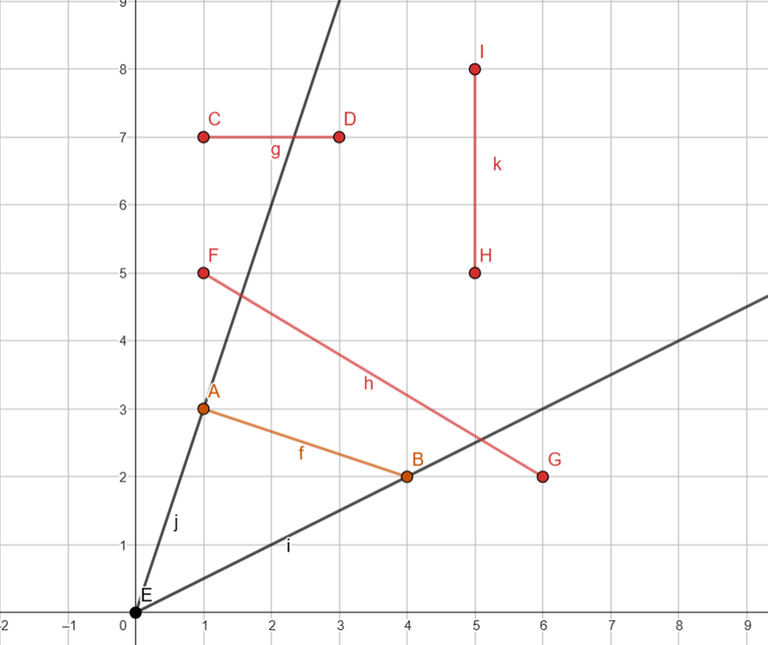
Although it is not explicitly mentioned, it is clear that rays were drawn from the origin to the vertices of the segment. Now, we can observe several things regarding the intersections: they will occur either along the rays or at the vertices of segment B. We will calculate the intersections as follows.
Case on the ray: Calculate the intersection between the line (origin, Ai) and the line (Bi, Bi+1 — Bi).
Case on the vertex of B: Calculate the intersection between the line (origin, Ai) and the line (Bi, Ai — Ai+1).
Once the intersection points are obtained, to calculate the scales, we can take the length of the intersection vector and divide it by the length of the vector of A with which the intersection was calculated. Sort them and return the resulting interval.
I will leave the cases where the origin and the vertices Ai and Ai+1 are collinear for last.
That's correct! Once the ranges are obtained, we can sort them and iterate through them to look for a gap in all of them (which should be at the endpoint of some range), right?
Now, when we take an endpoint of a range, can we be sure that the segment is completely contained within that scale? If we have two ranges, [e_0, f_0] and [e_1, f_1], and we know that f_0 is strictly smaller than e_1, we can confirm that it is fully contained with scale e_1 (It doesn't necessarily have to be completely contained; it can also be entirely outside. However, it can be handled this way and considered in the final sweep, because when a segment is entirely outside while the polygon is not, at least one segment is intersected). If f_0 is strictly greater, we know that it will not be contained. In the case where f_0 equals e_1, we have two possibilities to consider.
Looking at the image below, If the polygon belongs to D or N, but not both at the same time, and D is present, the segment (K, L) will not be completely contained along the segment (C, D). It will start intersecting when it leaves (C, D) and begins to intersect with the segment (D, E), but it will be fully contained as soon as it passes through point D. On the other hand, if N belongs to the polygon, the same scenario will occur with the segments (C, N) and (N, E), but the segment will not be fully contained when it passes through N.

To solve this, what we will do is for our range [e_0, f_0] and [e_1, f_1], if f_0 > e_1, we will combine these ranges into [e_0, max(f_0, f_1)]. If f_0 = e_1, then we will check if the segment (from which the scales were calculated) at scale f_0 is fully contained. In this case, we will not combine the ranges. If it is not contained, we will combine them. If f_0 < e_1, we will not combine the ranges.
Yeah, ignoring some implementation details, we can now merge all the ranges and perform a sweep to find a point that is not completely contained in any range, thereby obtaining the answer, right? Well, we left a small case earlier.
It is worth noting that, even without fully considering this case, my algorithm still achieved AC (yes, these are definitely weak cases).
We can have 4 cases, so let's start with the simplest one.
Case 1:
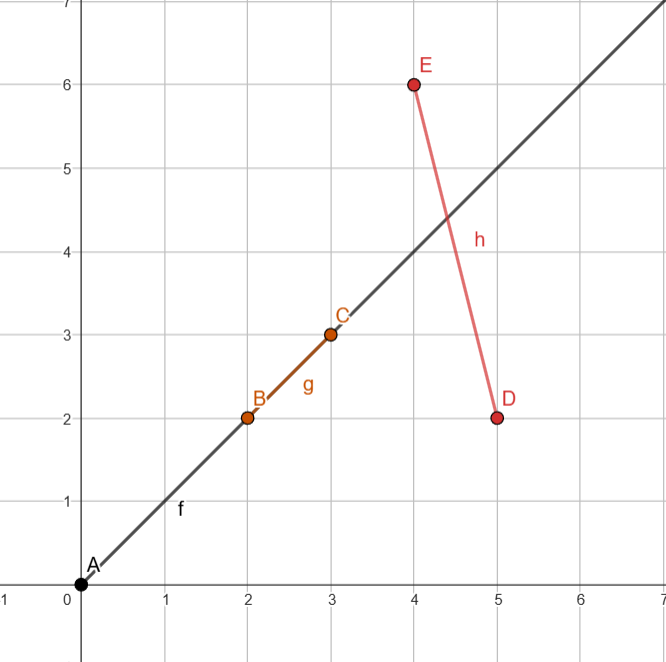
We know that the segment (B, C) will intersect with the segment (D, E) from the moment the closest point between points B and C aligns with the segment (D, E) until the closest point on the segment does so.
Case 2 & 3:
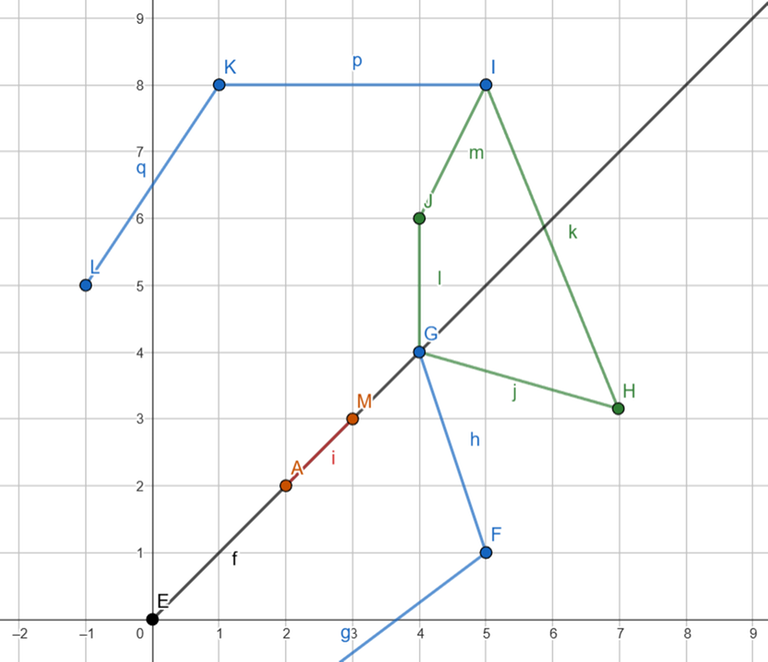
We can observe two things when it passes through the endpoint of a segment: whether it moves outside or inside. For our purpose, we will check the orientation of the next point relative to the intersection point. This will allow us to determine whether we should apply the same technique as in case 1 or ignore the point.
Case 4:
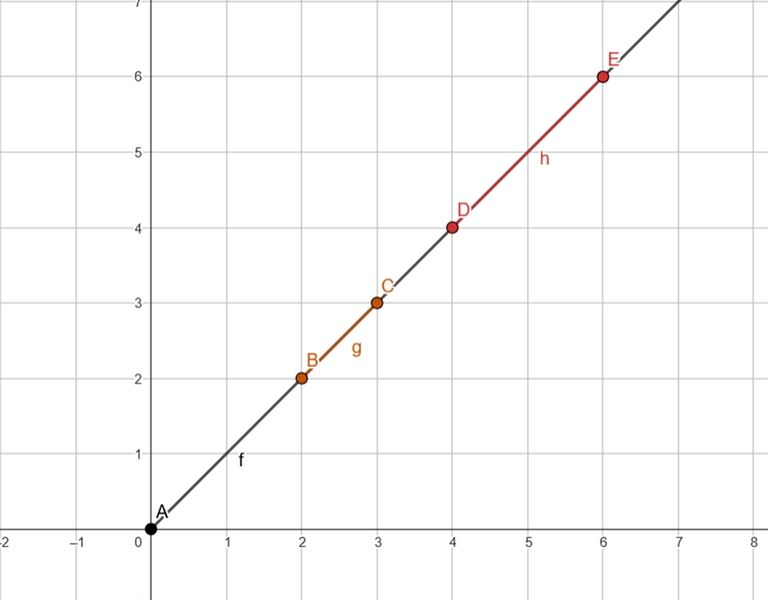
According to what we have been discussing, this is a case that we should simply ignore, meaning it never becomes completely outside, and that is true. However, it doesn't hurt to clarify this.
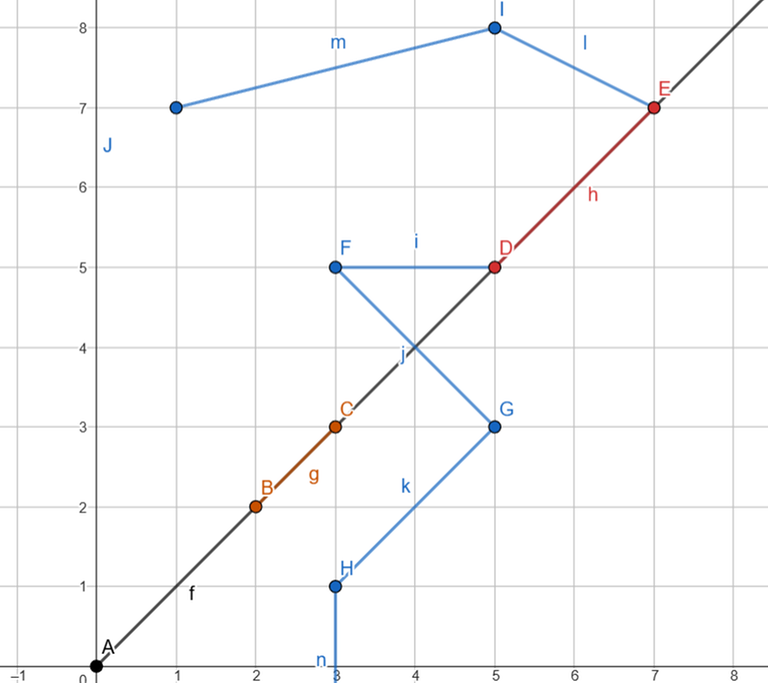
Just to expand on cases 2 and 3, we need to be careful when our intersection point, relative to the ray and the segment, is any of the vertices, and also consider the orientation of the next point. Although one could choose to directly handle the case where the segment and the ray are parallel.
Finally, with all the cases studied, we can perform the sweep and obtain the answer.
Analyzing the complexity, we will create at most m intervals for each of the n segments, and for each interval start, we will check if it is completely contained. This results in a complexity of $$$O(n * m * m)$$$, or equivalently, $$$O(n^3)$$$.
It is worth noting that the evaluations during the contest were not compromised because the official idea works in cases in the contest.
Musical recommendation: New Kid in Town ^^










