2048A - Kevin and Combination Lock
Author: Little09
How much does the number decrease when we remove two consecutive $$$3$$$ s?
2048A - Kevin and Combination Lock
When we transform $$$\overline{x33y}$$$ into $$$\overline{xy}$$$ (where $$$x$$$ and $$$y$$$ are decimal numbers), the actual value changes from $$$10^{p+2} \cdot x + 33 \cdot 10^p + y$$$ to $$$10^p \cdot x + y$$$. The decrease is $$$99 \cdot 10^p \cdot x + 33 \cdot 10^p$$$. It is easy to see that $$$33 \mid (99 \cdot 10^p \cdot x + 33 \cdot 10^p)$$$. Therefore, we can replace the operation of removing two consecutive $$$3$$$ s with a series of $$$-33$$$ operations.
Hence, we only need to determine whether $$$x$$$ can be reduced to $$$0$$$ using a series of $$$-33$$$ operations, which is equivalent to checking whether $$$x \bmod 33$$$ equals zero.
Author: wsyear
If the permutation is sufficiently long, what is the maximum number of length $$$k$$$ subintervals where the minimum value is $$$1$$$?
2048B - Kevin and Permutation
In the entire permutation, at most $$$k$$$ subintervals can contain $$$1$$$. Similarly, at most $$$k$$$ subintervals can contain $$$2, 3, \ldots$$$. To maximize the number of subintervals where the minimum value is as small as possible, we use the following construction:
For the remaining positions, we can fill them arbitrarily with all values from $$$\lfloor \frac{n}{k} \rfloor + 1$$$ to $$$n$$$. It is easy to prove that this construction minimizes the answer.
2048C - Kevin and Binary Strings
Author: Little09
Is there a substring that must always be selected for all strings?
The substring $$$[1,n]$$$ must be selected. Can we determine the length of the other substring?
Pay special attention to the case where the entire string consists of only $$$1$$$ s.
2048C - Kevin and Binary Strings
To maximize the XOR sum of the two substrings, we aim to maximize the number of binary digits in the XOR result. To achieve this, the substring $$$[1,n]$$$ must always be selected. Suppose the first character of the other substring is $$$1$$$. If it is not $$$1$$$, we can remove all leading zeros.
Next, find the position of the first $$$0$$$ in the string from left to right. We want this position to be flipped to $$$1$$$, while ensuring that the $$$1$$$s earlier in the string are not changed to $$$0$$$s. Therefore, let the position of the first $$$0$$$ be $$$p$$$. The length of the other substring must be $$$n-p+1$$$. By enumerating the starting position of the other substring and calculating the XOR sum of the two substrings linearly, we can take the maximum value. The time complexity of this approach is $$$O(n^2)$$$.
If the entire string consists only of $$$1$$$s, selecting $$$[1,n]$$$ and $$$[1,1]$$$ can be proven to yield the maximum XOR sum among all possible choices.
Interesting fact: This problem can actually be solved in $$$O(n)$$$ time complexity. Specifically, observe that the other substring needs to satisfy the following conditions: its length is $$$n-p+1$$$, and its first character is $$$1$$$. Thus, its starting position must be less than $$$p$$$. This implies that the length of the prefix of $$$1$$$s in the other substring can be chosen from the range $$$[1, p-1]$$$. We aim to flip the first segment of $$$0$$$ s in the original string to $$$1$$$ s, while ensuring that the $$$1$$$ immediately after this segment of $$$0$$$ s remains unchanged. Let the length of the first segment of $$$0$$$ s be $$$q$$$. Then, the length of the prefix of $$$1$$$ s in the other substring must be $$$\min(p-1, q)$$$, and the starting position can be determined efficiently.
When preparing the contest and selecting problems, we determined that the $$$O(n)$$$ solution would be too difficult for a Problem C. Therefore, the problem was designed with an $$$O(n^2)$$$ data range to make it more accessible.
2048D - Kevin and Competition Memories
Author: cmk666
You can ignore all contestants with a rating lower than yours; this does not affect the answer.
You are the contestant with the lowest rating, so any problem you can solve can also be solved by everyone else. Thus, your ranking in a competition only depends on the easiest problem you cannot solve.
Use greedy algorithm.
2048D - Kevin and Competition Memories
Read all the hints.
First, remove all contestants with a rating lower than yours, making you the contestant with the lowest rating. Since any problem you can solve can also be solved by everyone else, this does not affect your ranking. These problems can effectively be treated as having infinite difficulty.
At this point, you cannot solve any problem, so your ranking in a competition is given by $$$(1 + $$$ the number of contestants who solve at least one problem in that competition $$$)$$$. Therefore, we only need to focus on the easiest problem in each competition.
Precompute, for each problem, the number of contestants who can solve it, denoted as $$$c_i$$$. This can be done by sorting the contestants by rating and the problems by difficulty, then using a two-pointer or binary search approach to compute $$$c_i$$$.
The remaining task is: given $$$c_i$$$, divide all $$$c_i$$$ into $$$\lfloor \frac{n}{k} \rfloor$$$ groups, each containing $$$k$$$ elements, and minimize the sum of the maximum values in each group. This can be solved using a greedy algorithm: sort $$$c_i$$$ in ascending order, and for a given $$$k$$$, the answer is $$$(c_k+1) + (c_{2k}+1) + \dots$$$. The brute force calculation is bounded by the harmonic series, and combined with sorting, the time complexity is $$$O(n \log n + m \log m)$$$.
2048E - Kevin and Bipartite Graph
Author: Little09
It can be observed that the larger $$$m$$$ is, the harder it is to satisfy the conditions. Try to find an upper bound for $$$m$$$.
2048E - Kevin and Bipartite Graph
The graph has a total of $$$2nm$$$ edges, and each color forms a forest. Therefore, for any given color, there are at most $$$2n + m - 1$$$ edges. Thus, the total number of edges cannot exceed $$$(2n + m - 1)n$$$. This gives the condition: $$$(2n+m-1)n\ge 2nm$$$. Simplifying, we find $$$m \leq 2n - 1$$$.
Next, we only need to construct a valid case for $$$m = 2n - 1$$$ to solve the problem.
In fact, this is easy to construct. Since each right-side vertex has a degree of $$$2n$$$, and there are $$$n$$$ total colors, let each color have exactly $$$2$$$ edges. For any given color, this is equivalent to choosing two left-side vertices to connect (ignoring the existence of the right-side vertices). After $$$2n - 1$$$ connections, the left-side vertices need to form a tree. It turns out that connecting the left-side vertices into a chain suffices. During construction, we can cycle the colors of the first right-side vertex. For example, for $$$n = 4$$$ and $$$m = 7$$$, the result looks like this:
1 4 4 3 3 2 2
1 1 4 4 3 3 2
2 1 1 4 4 3 3
2 2 1 1 4 4 3
3 2 2 1 1 4 4
3 3 2 2 1 1 4
4 3 3 2 2 1 1
4 4 3 3 2 2 1
Thus, a simple construction method is as follows: for left-side vertex $$$i$$$ and right-side vertex $$$j$$$, the color of the edge connecting them is given by:
Author: wsyear
Can you find a strategy such that only $$$n$$$ intervals might be operated on?
By operating on the entire sequence in each step, the answer can be made $$$\leq 63$$$.
2048F - Kevin and Math Class
Construct a min Cartesian tree for the sequence $$$b$$$. It is easy to observe that we will only operate on the intervals defined by this Cartesian tree.
- Proof: For any $$$b_x$$$, find the last $$$b_p \leq b_x$$$ on its left and the first $$$b_q < b_x$$$ on its right. If we want to divide the interval by $$$b_x$$$, the operation interval cannot include both $$$p$$$ and $$$q$$$. At the same time, choosing the largest possible interval is always optimal. Hence, the operation interval must be $$$[p+1, q-1]$$$. All such intervals are exactly the intervals corresponding to the Cartesian tree.
To solve the problem, we can use DP on the Cartesian tree. Let $$$f_{u,i}$$$ represent the minimum possible maximum value of $$$a_x$$$ within the subtree rooted at $$$u$$$ after performing $$$i$$$ operations on all positions within that subtree.
When merging, suppose the two child subtrees of $$$u$$$ are $$$ls$$$ and $$$rs$$$. The transition can be written as:
Then consider division at the position corresponding to $$$b_u$$$, which updates the DP state:
Since operating on the entire sequence repeatedly can ensure that $$$\log_2(\max(a_i)) \leq 63$$$ operations suffice, the second dimension of the DP state only needs to be defined for $$$0 \sim 63$$$. Thus, the time complexity for this approach is $$$O(n \log^2 a)$$$.
The bottleneck of this approach lies in merging the DP states of the two subtrees. Observing that $$$f_{u,i}$$$ is monotonically non-increasing, the $$$\min-\max$$$ convolution for $$$f_{ls,i}$$$ and $$$f_{rs,i}$$$ is equivalent to merging two sequences using a merge sort-like approach. This reduces the merging complexity to $$$O(\log a)$$$.
Consequently, the overall complexity becomes $$$O(n \log a)$$$, which is an optimal solution.
Author: cmk666
Can the left-hand side be less than the right-hand side?
Consider the positions where the extremes are reached in the expression. What properties do they have?
Use the principle of inclusion-exclusion.
Apply the Binomial Theorem.
2048G - Kevin and Matrices
Let us assume the left-hand side attains its maximum at position $$$L$$$, and the right-hand side attains its maximum at position $$$R$$$.
For any $$$L, R$$$, let $$$P$$$ be the position in the same row as $$$L$$$ and the same column as $$$R$$$. Then we have $$$a_L \geq a_P \geq a_R$$$, which implies $$$a_L \geq a_R$$$. Hence, we only need to consider cases where $$$a_L = a_R$$$.
Now, consider positions where both sides attain their maximum value, denoted as $$$S$$$. Positions in $$$S$$$ are the maximum in their respective column and the minimum in their respective row. For any two positions $$$P, Q$$$ in $$$S$$$ that are not in the same row or column, we can observe that the positions in the same row as $$$P$$$ and the same column as $$$Q$$$, and vice versa, can also attain the maximum value. By induction, we can conclude that $$$S$$$ forms a subrectangle.
Next, enumerate the maximum value $$$k$$$ and the size of $$$S$$$, denoted by $$$i \times j$$$. The constraints are as follows: all remaining elements in the rows of $$$S$$$ must be $$$\leq k$$$, and all remaining elements in the columns of $$$S$$$ must be $$$\geq k$$$. Using the principle of inclusion-exclusion, we derive:
The naive approach is $$$O(nmv)$$$, which is computationally expensive. Let us simplify:
This resembles the Binomial Theorem. To simplify further, add and subtract the term for $$$j=0$$$:
Thus, the problem can be solved in $$$O(nv\log m)$$$ time.
2048H - Kevin and Strange Operation
Author: JoesSR
Consider how to determine if the $$$01$$$ string $$$t$$$ can be generated.
Try designing a DP that only records the useful variables.
Optimize using data structures or improve the complexity of the transitions.
2048H - Kevin and Strange Operation
Assume that after performing several operations on the $$$01$$$ string $$$s$$$, we get the $$$01$$$ string $$$t$$$. It’s not hard to notice that each element in $$$t$$$ corresponds to the $$$\max$$$ of a subset of elements from $$$s$$$. Further observation shows that this subset must form a continuous segment, so we can express $$$t_i$$$ as $$$\max\limits_{k=l_i}^{r_i} s_k$$$.
Initially, $$$t = s$$$, so all $$$l_i = r_i = i$$$. Suppose the current length of string $$$t$$$ is $$$m$$$, corresponding to two sequences $$$l$$$ and $$$r$$$. If an operation is performed at position $$$p$$$ where $$$1 \le p \le m$$$, the new sequence $$$t'$$$ will correspond to two sequences $$$l'$$$ and $$$r'$$$. Then, since for $$$1 \le i < p$$$, we have $$$t'_i=\max(t_i,t_{i+1})$$$, and for $$$p \le i < m$$$, $$$t'_i=t_{i+1}$$$, it can be observed that for $$$1 \le i < p$$$, we have $$$l'_i=l_i,r'_i=r_{i+1}$$$, and for $$$p \le i < m$$$, $$$l'_i=l_{i+1},r'_i=r_{i+1}$$$. If we only focus on the change of sequences $$$l$$$ and $$$r$$$ to $$$l'$$$ and $$$r'$$$, it is equivalent to deleting the values $$$l_p$$$ and $$$r_1$$$.
Thus, performing $$$k$$$ operations starting from the sequence $$$s$$$, the resulting sequence $$$t$$$ will correspond to the sequences $$$l$$$ and $$$r$$$, where $$$l$$$ is obtained by deleting any $$$k$$$ values from $$$1$$$ to $$$n$$$, and $$$r$$$ is the sequence from $$$k+1$$$ to $$$n$$$.
Now, let's consider how to determine if the $$$01$$$ string $$$t$$$ can be generated. By reversing $$$t$$$ to get $$$t'$$$, the task becomes finding $$$n \ge p_1 > p_2 > \dots > p_k \ge 1$$$ such that for all $$$1 \le i \le k$$$, we have $$$t'_i=\max\limits_{k=p_i}^{n-i+1}s_k$$$. A clearly correct greedy strategy is to choose $$$p_i$$$ in the order $$$i=1 \sim k$$$, always selecting the largest possible value.
Now consider performing DP. Let $$$dp_{i,j}$$$ represent how many length-$$$i$$$ $$$01$$$ strings $$$t$$$ can be generated such that after running the above greedy algorithm, $$$p_i$$$ exactly equals $$$j$$$. We assume that $$$p_0 = n+1$$$ and the boundary condition is $$$dp_{0,n+1} = 1$$$. We now consider the transition from $$$dp_{i-1,j}$$$ to $$$dp_{i,*}$$$:
- If $$$s[j-1, n-i+1]$$$ already contains $$$1$$$, then the $$$i$$$-th position in the reversed $$$t$$$ must be $$$1$$$, and it must be the case that $$$p_i = j-1$$$, so we add $$$dp_{i,j-1}$$$ to $$$dp_{i-1,j}$$$.
- If $$$s[j-1, n-i+1]$$$ does not contain $$$1$$$, the $$$i$$$-th position in the reversed $$$t$$$ can be $$$0$$$. If it is $$$0$$$, then it must be the case that $$$p_i = j-1$$$, and we add $$$dp_{i,j-1}$$$ to $$$dp_{i-1,j}$$$; if we want the $$$i$$$-th position in the reversed $$$t$$$ to be $$$1$$$, we need to find the largest $$$pos \le n-i+1$$$ such that $$$s_{pos} = 1$$$, and then set $$$p_i = pos$$$, adding $$$dp_{i,pos}$$$ to $$$dp_{i-1,j}$$$.
Both types of transitions can be considered as adding $$$dp_{i,j-1}$$$ to $$$dp_{i-1,j}$$$, then finding the largest $$$pos \le n-i+1$$$ where $$$s_{pos} = 1$$$, and for all $$$j-1 > pos$$$ (i.e., $$$j \ge pos+2$$$), adding $$$dp_{i,pos}$$$ to $$$dp_{i,j}$$$.
The first type of transition can be viewed as a global shift of the DP array, while the second type requires calculating a segment suffix sum of the DP array and then performing a point update. This can be done efficiently using a segment tree in $$$O(n \log n)$$$ time for all transitions.
The final answer is the sum of all $$$1 \le i \le n, 1 \le j \le n$$$ of $$$dp_{i,j}$$$. Using a segment tree for maintenance, we can also query the sum of each entry of $$$dp_i$$$ in $$$O(1)$$$ time (by setting to zero those entries where $$$dp_{i-1,1}$$$ is out of range after the shift).
Since the transitions have better properties, it's actually possible to solve the problem cleverly using prefix sums in $$$O(n)$$$ time without needing complex data structures, but that is not strictly necessary.
2048I1 - Kevin and Puzzle (Easy Version)
Author: Little09
Consider the leftmost and rightmost characters, and recursively construct the sequence.
2048I1 - Kevin and Puzzle (Easy Version)
Lemma: Suppose the largest value filled is $$$mx$$$, and the number of distinct values is $$$c$$$. Let $$$d = c - mx$$$. Then, $$$d = 0$$$ or $$$d = 1$$$.
Proof: Clearly, $$$c \le mx + 1$$$. If $$$c < mx$$$, observe where $$$mx$$$ is placed, and a contradiction arises.
Now, consider the leftmost and rightmost characters in sequence $$$s$$$:
- If they are
LandR, we can see that both positions must be filled with $$$0$$$, and no other position can be filled with $$$0$$$. For internal positions, whetherLorR, $$$0$$$ counts as a distinct number. Therefore, we can remove these two positions, recursively solve for the remaining part, add $$$1$$$ to all numbers, and then place a $$$0$$$ at both ends. - If both are
L, the leftmostLmust be $$$0$$$. Suppose the rightmostLis filled with $$$x$$$. It is easy to prove that $$$x$$$ cannot be placed in internal positions. For internal positions, whetherLorR, either $$$0$$$ or $$$x$$$ is counted as a distinct number. So, as in the previous case, we remove the two positions, recursively solve for the remaining part, add $$$1$$$ to all numbers, and then add $$$0$$$ and $$$x$$$ at both ends. The value of $$$x$$$ must be the number of distinct values inside plus 1. This condition is equivalent to the internal region satisfying $$$d = 1$$$. - If both are
R, the analysis is the same as for theLandLcase. - If the leftmost character is
Rand the rightmost character isL, a simple construction is to fill everything with $$$1$$$. In this case, no $$$0$$$ will appear, so this case can only correspond to $$$d = 0$$$.
We recursively remove the leftmost and rightmost characters, solve for the inner region, add $$$1$$$ to all of them, and place $$$0$$$ and $$$x$$$ at both ends.
Now, consider how $$$d$$$ changes:
- For the
LRcase, $$$d$$$ remains unchanged. - For
LLorRR, the internal region must satisfy $$$d = 1$$$. - For
RL, the entire region results in $$$d = 0$$$.
Therefore, consider the outermost RL. If it contains LL or RR inside, there is no solution.
Otherwise, a solution always exists, and it can be easily constructed based on the above process, the time complexity is $$$O(n)$$$.
2048I2 - Kevin and Puzzle (Hard Version)
Author: Little09
Only the case where the characters on both sides are RL in the simple version needs to be counted. In fact, the numbers at these two positions, RL, must be the same.
Let the number at the RL positions be $$$m$$$, and enumerate the rightmost R position $$$x$$$ that is filled with $$$m$$$, and the leftmost L position $$$y$$$ that is filled with $$$m$$$.
The case where $$$x > y$$$ is easy to resolve. For the case where $$$x < y$$$, analyze the necessary and sufficient conditions for it to hold.
For the final transformed condition, use bitset or convolution to complete the counting.
2048I2 - Kevin and Puzzle (Hard Version)
According to the easy version, we can see that most cases have very few solutions because for LR, LL, and RR, after filling in the inner part, the outer layer only has one unique way to fill. Therefore, if there is no RL layer, the answer must be $$$1$$$.
Next, consider the case where RL is present. Let’s assume that RL is the outermost pair of characters.
It can be proved that the numbers at the R and L positions in this RL must be the same. The specific proof is omitted here, but readers can prove this for themselves easily.
Let this common value be $$$m$$$. Then, enumerate the rightmost R position $$$x$$$ filled with $$$m$$$ and the leftmost L position $$$y$$$ filled with $$$m$$$. Now, let’s discuss the relationship between $$$x$$$ and $$$y$$$:
If $$$x > y$$$, it can be observed that all
Ls to the right of $$$x$$$ must be filled with $$$m$$$, and allRs to the right of $$$x$$$ have only one way to be filled. The same applies for $$$y$$$. For this case, we can directly enumerate $$$m$$$, then determine the unique positions for $$$x$$$ and $$$y$$$, and check if $$$x > y$$$.If $$$x < y$$$, at this point, all
Rs to the left of $$$x$$$ must be filled with $$$m$$$, and theLs to the left of $$$x$$$ have only one way to be filled. Similarly for the right side of $$$y$$$. Now, consider the section between $$$(x, y)$$$. Clearly, $$$m$$$ must not appear in the middle, so we can delete $$$x$$$ and allRs to its left, as well as $$$y$$$ and allLs to its right (i.e., remove all positions where the value is $$$m$$$). The resulting sequence is called the remaining sequence. After removing these characters, we solve for the remaining sequence, then add $$$1$$$ to all the numbers obtained, and finally, add all positions filled with $$$m$$$.
Below is an example of an initial sequence, where the red characters are $$$x$$$ and $$$y$$$, and the omitted part is the section between $$$(x, y)$$$.

Below is the corresponding remaining sequence, with $$$*$$$ representing the original sequence positions of $$$x$$$ and $$$y$$$.
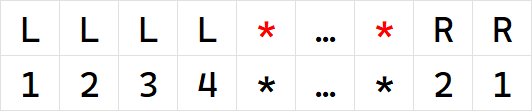
After filling the remaining sequence, we need to analyze the conditions for adding all positions filled with $$$m$$$: we divide the remaining sequence into three parts: "left", "middle", and "right", with the positions of $$$x$$$ and $$$y$$$ as boundaries, where the left part contains onlyLs, and the right part contains onlyRs. The condition to be satisfied is that let the total number of colors in the "left-middle" part be $$$c_1$$$, and the total number of colors in the "middle-right" part be $$$c_2$$$, then we need $$$m = c_1 + 1 = c_2 + 1$$$. Additionally, $$$m$$$ must not appear in the remaining sequence. This restriction is equivalent to requiring both the "left-middle" and "middle-right" parts to satisfy $$$d = 1$$$. It can be concluded that the remaining sequence satisfies $$$d = 1$$$. For the condition $$$c_1 = c_2$$$, it is easy to see that it is equivalent to: let $$$z$$$ be the larger of the counts of the left and right parts, then the first $$$z$$$ characters of the remaining sequence must all beL, and the last $$$z$$$ characters must all beR.
The final necessary and sufficient condition is: let $$$x$$$ have $$$a$$$Ls to the left, and $$$y$$$ have $$$b$$$Rs to the right. Without loss of generality, assume $$$a \ge b$$$. Remove the substring between $$$(x, y)$$$ (not including $$$x$$$ and $$$y$$$). This remaining substring needs to satisfy that the last $$$a-b$$$ characters areRs, and after removing these $$$a-b$$$Rs, the resulting string must satisfy $$$d = 1$$$, meaning there is noRLsituation when taking the first and last characters. Since $$$d = 1$$$, if the remaining sequence satisfies this condition, there will be exactly one way to fill it.
Finally, we only need to count the cases separately. The case where $$$x > y$$$ can be counted in $$$O(n)$$$, for the case where $$$x < y$$$, without loss of generality, assume $$$a \ge b$$$, we can enumerate $$$y$$$, calculate the length of the longest consecutive Rs before $$$y$$$, denoted as $$$cnt$$$, so the restriction on $$$a$$$ becomes $$$b \le a \le b + cnt$$$.
- When $$$cnt = 0$$$, the value of $$$a$$$ is fixed, but the corresponding $$$x$$$ can be chosen from any position in a consecutive block of
Rs. We find that because $$$cnt = 0$$$, i.e., the position before $$$y$$$ is filled withL, then the position after $$$x$$$ cannot be filled withR, so $$$x$$$ can only be chosen as the lastRin the consecutiveRblock. - When $$$cnt > 0$$$, we only need to enumerate the values of $$$x$$$. It is easy to see that each $$$x$$$ will be counted at most $$$2$$$ times.
Through the above observations, we only need to enumerate $$$O(n)$$$ pairs of $$$x$$$ and $$$y$$$ and check whether they increase the answer by $$$1$$$. That is, the answer is at the $$$O(n)$$$ level.
The last problem is: for each given interval $$$[l, r]$$$, we need to check if there is any RL situation when taking the first and last characters of this string.
A simple solution is to use a bitset to maintain, for example, by scanning $$$r$$$ from small to large, and maintaining the existence of RL for each $$$l + r$$$. The time complexity of this approach is $$$O(\frac{n^2}{\omega})$$$, which can be handled by this problem.
If using block convolution, a more optimal complexity can be achieved. In fact, if further exploring the properties, the time complexity can be reduced to $$$O(n \log^2 n)$$$ (requiring convolution), which you can explore on your own if you are interested.










first
I was one $$$=$$$ sign off from getting $$$E$$$ lol
Haha me too. I wrote
> 2*ninstead of>= 2*nlol. Now first time losing ratingI think the $$$O(n)$$$ solution for C is quite interesting. Why not split it into a C2?
I agree
that would have been still better than E problem.
Can anyone please guess the error because of which my code is giving wrong answer on the 7th test case.
I was trying to solve C by explicitly taking XOR from numbers (i.e. binary transformed into decimal) and obviously ran out of memory. And then I came to the $$$O(n)$$$ solution.
(edited)
bro skipped a step from taking the xor of numbers of 5000 digits to finding the optimal solution
Even I solved C in O(n). Was able to prove my hypothesis on working with first 0 and first 1 after first 0.
Lol I directly coded the O(n) solution :D Slight observation but I was able to get that correct in one go.
First time ever i solve 5 problems in a div2, i think D is very cool, and i kinda guessed E but good contest overall
*div1
YES!! I also enjoyed Problem D
It's my first time too :)
great contest and tutorial :)
Can anyone explain why my D Solution is too slow?
O(m^2) solution is going to give you TLE as m<=3e5
Thanks for pointing that out. Got tunnel visioned. Later I got this accpeted Here
great contest tho I find it wired that F requires such complex data structure (probably it isn't wired and I just lack experience)
It's not complicated structure for F.
Id say a min cartesian tree is complicated though?
For a Div1D/Div2F no.
Honestly a min Cartesian Tree is just a fancy way of refering to the classic problem of finding for each element its first lower neighbours on the left/right.
Now you can say that each element is the node corresponding to an interval, and all you need to add is to compute the two childs in the tree (which corresponds to the interval splitted by the minimum value), which requires a bit of thinking but no complicated code.
Finally to manage the DP in the tree you can do simply dfs using the indices of intervals and never explicitly construct the tree, like you would do in a divide and conquer approach.
All in all it might be a complex idea but it can be implemented easily (you can check my submission if you'd like (which is $$$O(nlog^2)$$$ should you wonder))
Special Thanks to cmk666 for the nice problem 2048D - Kevin and Competition Memories
one more div2 contest where i can't solve more than 3 questions.
how should i practice to solve question D in div 2 contests? thanks in advance
bro It's div (1 + 2)
is div(1+2) D harder than div2 D?
Anyone tried solving E with below approach.
Each edge can be represented as ordered pair ( i , j ) . where 'i' belongs to left side, and 'j' belongs to right side.
Now, we have total of 2 * n * m such ordered pairs. each of these edge can be actually convert into a vertex. since our graph is bipartite, after we travel one of our edge, next edge direction will be opposite ( if we travel current edge from left to right, next edge we must travel right to left )
=> if I am going from (i,j1) to (i,j2) , i will try to give available color to (i,j2) and then I will keep 'j2' constant and try to find some valid 'i' which is not yet colored and try to color it.
Now start DFS from (1,1) , and if its odd iteration of the we will go from left to right, if it is even iteration, we will go from right to left.
When we go from left to right , we will keep 'i' constant and loop over all the 'j' in the ordered pair ( i , j ) .
When we go from right to left, we will keep 'j' constant and loop over all the 'i'.
We will try to basically color this graph of 2 * n * m vertices,,, with 'n' colors. I tried this approach, but don't know, why does it fail ?
E made me sad.
E made me mad
So true :(
Can anyone please guess the error because of which my code is giving wrong answer on the 7th test case.
why post this twice?
G is a nice one! ❤️
For F, the constraints don't cut the $$$n \cdot \log^2(a)$$$ solution, but also make it harder for people who are careful.
I spent extra time to optimize out a $$$\log(a)$$$ factor just like the editorial because $$$n \cdot \log^2(a) \approx 8 \cdot 10^8$$$.
If instead the time limit was greater or $$$a = 10^9 \implies n \cdot \log^2(a) \approx 2 \cdot 10^8$$$, I would definitely go for this solution and not waste time. Since I optimized, I failed to finish F by a few minutes.
I didn’t pass with log^2 so it’s kinda a gamble…
Was curious about F's solution and heard for the first time about min cartesian tree!! Anyone have any good resources to learn more about it?
https://youkn0wwho.academy/topic-list/cartesian_tree Check this out
can someone please help me with this solution. It fails for tc5
Just replace
std::bitset<32>withstd::bitset<5007>and the solution passes: 297364634. In the problem, the string length can be up 5000, so the bitset should be capable to store at least 5000 bits.Why is this code for D failing?
I had a similar implementation which worked : 297364236 I dont think you can ignore problems with lower difficulty than Kevin's skill since you can use them to "pad" contests
bro im gonna be honest i dont even know what am im doing, could you explain what the greedy algorithm the editorial describes is doing ?
Consider a problem which has difficulty X such that X > Kevin's skill. Then if the number of people who can solve this problem are Y, this means that if you include this problem in a contest, at least Y people will be ahead of Kevin since Kevin can't solve it.
If the difficulty X is equal to or less than Kevin's skill, then no one will be able to get ahead of Kevin using only this problem, in which case the number of people ahead of Kevin is 0. So, for each problem P[i] you can calculate how many people can potentially get ahead of Kevin using only P[i] (say we call this value Ahead[i]).
Now you need to create K groups. Kevin's final ranking in a group will be max(all Ahead[i] values in the group) + 1. For example If the group has Ahead values 0 1 4, that means everyone solves the first problem, the second problem is solved by one person who is not Kevin and the third problem is solved by 4 people but not Kevin. This means that a total of 4 people are ahead of Kevin, giving Kevin 5th rank (Note that the person who solves the second problem is also among the people who solve the third problem, which is why we take max(Ahead[i])). The final answer is the sum of ranks across all groups.
Now in order to minimize the sum, you must minimize the max(Ahead[i]) in each group which you can do by greedily assigning K values with lowest Ahead[i] in the first group, next K lowest in next group and so on. So if Ahead array is 0 1 3 5 and K = 2, we make groups (0, 1) and (3, 5). The sum of ranks would be max(0,1) + 1 + max(3, 5) + 1 = 2 + 6 = 8
I hope this didn't confuse you even more lol
i got it bro tysmm
Wait I think I got it. When constructing the answer we need to take the k problems the least amount of people solved. So we get the k first problems after padding them out. Is this it? I still don't know how the solution doesn't raise TLE though
For each K from 1 to m, you start from (K-1)th index and increment by K as long as the index < m. So for K = 1, there are m operations. For K = 2, m/2 operations and so on which results in MLog(M) complexity. Hence no TLE
yeah turns out we're doing m * (1/1 + 1/2 + 1/3 + 1/4 + ... + 1 / m) operations which is the harmonic series sum thing the editorial mentions, which is log(n) for some reason so ok nice
For E, I found this paper which solves a slightly more general problem of coloring a complete bipartite graph into the minimum number of colors such that each color is a forest.
Can someone please help me out where I am going wrong with C: my submission
I get that the first substring will be the entire string, and the second substring will be of the length = length of complete string — position of first 0 from left. But since we only have to find out which such substring gives the maximum XOR, I take a different parameter called 'ans' in my solution and I claim that the substring which gives the higher 'ans' will also give the higher XOR value.
Here is how I am constructing 'ans': I am comparing the portion of two strings which is to be XOR'ed. Starting from the most significant bit, if the corresponding bit in both the strings are 0 and 1 respectively, I am incrementing ans by a larger value (and decrementing if the bits are 1 and 1 respectively since that will decrease XOR value). As I move from left to right, The value with which I increment/decrement ans decreases (since the right bits will have less contribution to the XOR value than the left bits). The substring which gives the maximum 'ans' value will also give me the maximum XOR value. But I am getting wrong answer on test case 2 itself and I am unable to figure out where I am going wrong! Please help
Maybe my implementation can help you:
Thanks for your code, I completely understood it. However, I still haven't understood what is wrong in my implementation.
I think your ans logic is flawed, say you have two candidates for strings, the first one has a better most significant bit and the other one has a worse most significant bit but every other bit is better in the second one. Maybe the way your ans is incremented makes the sum of the second one better than the first one if that makes sense
Ahh now I get it! I have been trying to figure out a flaw in my logic since the last 4 hours, only to find out it was this trivial :')
Thank you very much for pointing this out!
Please do not post entire solutions in the comments. Makes it very noisy to scroll through the comments. Paste submission links.instead.
I hate the fact, that I was debugging F for 40 minutes, because I was getting RTEs on test 3. There was some stupid stack overflow; the recursion was returning a big static object (488 bytes), and after changing it to return an 8 byte pointer, it started working; however, my memory usage was under 350MB, so it should have passed initially.
Edit: Codeforces DOES pass
-Wl,--stack=268435456to the linker, however it means the stack limit is always 256MiB regardless of the problem's memory limit. This is totally unreasonable.Original comment:
It is because codeforces's judging environment is Windows, and it seems that they don't pass
-Wl,--stask=xxxto the linker, which leads to a stack limit which is smaller than memory limit. I hope MikeMirzayanov could fix it, as more than one contestant faced it during contest time.Maybe the problem is that codeforces is passing exactly 256MB and ignoring the problem's memory limit, https://codeforces.net/blog/entry/121114 ?
Good contest,make me promote to IM :)
Little09 Can you elaborate on the $$$O(n\log^2n)$$$ solution for I2? Idk what block convolution is.
There is a solution of complexity $$$O(n\sqrt{\frac{n\log n}{\omega}})$$$. The general idea is to divide the sequence into chunks for every $$$B$$$ positions, and for each $$$l+r$$$ value find the $$$r$$$ that minimally satisfies the condition. If $$$l,r$$$ belongs to different blocks, enumerating the blocks of $$$r$$$ and then convolving this block with the prefixes tells us which $$$l+r$$$ occur, and then finding the smallest $$$r$$$ within the block. The case where $$$l,r$$$ belongs to the same block is easily solved. Finally, the bitset optimization is performed to obtain a complexity of $$$O(\frac{n^2}B\log n+\frac{nB}{\omega})$$$.
About $$$O(n\log ^2n)$$$ solution, it comes from JoesSR and it is more difficult and maybe I will add in the Editorial in a few days.
can someone tell me why it fails on test 3
Pls use spoiler, this comment is unnecessarily log.
so it can be optimized to $$$O(n)$$$?
CONGRATULATIONS! my friend chenlinxuan0226 reached CM after this contest!
"In fact, this is easy to construct"
Even after reading more than 5 times, above statement still hurts my soul.
I think it will be easy, if you make construction this way:
Our answer should satisfy the following property, if we fix two rows i.e., the nodes on the left side, there should not be greater than two columns of same colours.
Like this case where there are two columns of (1, 1) which forms cycle for a pair of nodes on left. So, it won't work.
1....1.....2
3....3.....4
1....1.....3
By trying out small cases and making construction based on this would be easy.
So, for (n, m = 2 * n — 1), you could always find a case, where there are no two columns of same colour for every possible pair of rows. And this also satisfies for all m <= 2 * n — 1 (Printing the array till m columns).
for n = 4
1 1 1 1 2 3 4
2 2 2 2 3 4 1
3 3 3 3 4 1 2
4 4 4 4 1 2 3
1 2 3 4 1 1 1
1 2 3 4 2 2 2
1 2 3 4 3 3 3
1 2 3 4 4 4 4
Why my stupid $$$\Theta(n\log^2 v)$$$ solution for F ran for just 827ms, can sb hack it or did it just run too fast because of constant factor? 297330202
got my first problem C !!!!
i somehow thought of the o(n) and not o(n^2) on C lol
Proof (for problem C) of why (1,n) is always one of the substring.
let leftmost '1' occurs at pth position(from right to left) no other substring can have (p+1)th position '1' hence can never exceed the xor of one pair created using (1,n) as one substring.
also 2^k> 2^(k-1)+ 2^(k-2)....... +2+1. so if you could get xor with all bits '1' and with length (p-1) it will still be smaller than which could be generated using (1,n) (pth position '1').
please correct me if i am wrong.
Can't we include visual explanation with images in editorial? then many more participants can upsolve the problems and can Improve, i usually find difficulty to understand the text solution.
Identity V?
Finally, after losing hope so many times. I can now understand "how to understand the problems". I may seem funny/absurd/weird to others, but I'm glad.
Also, it's a great contest. Registered for extra registration and able to understand questions. I almost got the C but missing a piece to complete. Way to go and learn. Hope for great learning !
I have a doubt in problem C, if the problem does not say that string starts with '1' does it will change the answer?
I yes how?
Well you always want one of the strings to be in the range of [the left most one,1]. So instead of solving on the entire string, you would first check the edge case of all 0s and then just solve the same thing on the substring from where the first 1 ocurrs
Yeah..
Can someone help me identify where I went wrong in this solution 297315319? I believe my solution has a time complexity of $$$O(n^2)$$$, yet I am experiencing a TLE for test case 21. Any assistance would be greatly appreciated.
First, I identified the index $$$(idx)$$$ where the first zero appears in the string. After that, I iterated through all the characters that have an index less than $$$(idx + 1)$$$. For each character, I calculated the XOR of the original string with the substring starting at that character $$$(i)$$$ and extending to a length of $$$n - idx$$$. And stored the maximum XOR result.
I had so much fun doing C, firstly I devised O(n^2) solution then I noticed I can use concept of MSB once again and voila got O(n) solution. Spent 1 hour on this though.