Formal proof on how many weapon levels can be neglected.
Let us take k = 1 and denote the stopping time of obtaining a weapon of cost i as 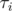 . Then
. Then
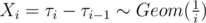 independent
independent
We can bound from below the geometric distriubtion by uniform one, in a sense that
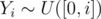 independent
independent
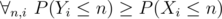
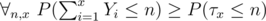
where 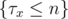 is exactly an event in which we eventually obtain a weapon of level x. Now let us present the probability space of Y1, .., Yx as Ω = [0, 1] × [0, 2] × .. × [0, x] which is a hypercuboid with volume x!, therefore probability measure P has density
is exactly an event in which we eventually obtain a weapon of level x. Now let us present the probability space of Y1, .., Yx as Ω = [0, 1] × [0, 2] × .. × [0, x] which is a hypercuboid with volume x!, therefore probability measure P has density 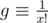 in lebesgue measure. It is easy to see that
in lebesgue measure. It is easy to see that 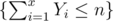 is contained in a hypercone of lebesgue volume
is contained in a hypercone of lebesgue volume 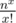 . By taking into consideration the density g, we get an upper bound
. By taking into consideration the density g, we get an upper bound
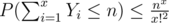
Now back to the original task. Let us denote the total profit from selling the weapons as T ≤ n2. We want the following expectation to be small:
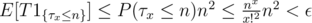
For n = 105 and ε = 10 - 9, using the formula above we can check that x = 900 is enough.










