Здраствуйте.
Я нашел описание min cost max flow, где описан процесс выдачи потенциалов: http://rain.ifmo.ru/cat/view.php/vis/graph-flow-match/min-cost-max-flow-2009/algorithm
Там не доказывается, что выбор потенциалов описанных образом позволит избежать появления ребер отрицательного веса.
Пусть у нас такая остаточная сеть. Вершина 4 -исток. Вершина 5 — сток: 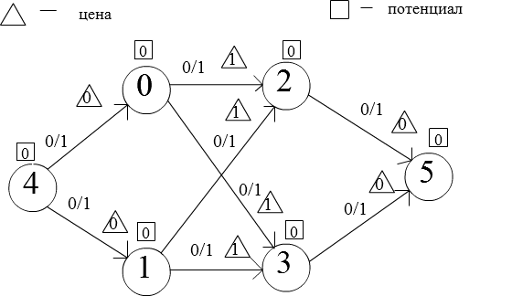
Найдем кратчайший путь веса 1 4->0->2->5 и протолкнем через него одну единицу потока. Получим такую остаточную сеть: 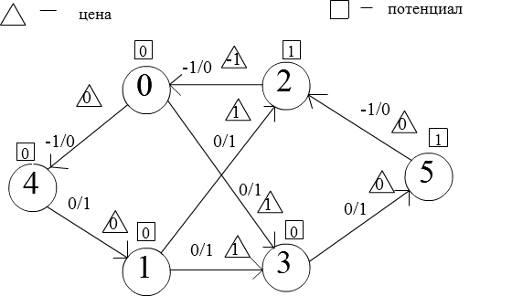
Найдем такой кратчайший по весу путь:
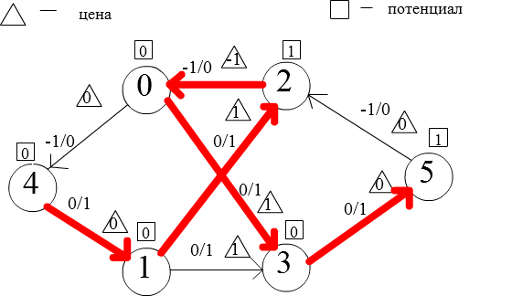
Он действительно кратчайший
4->1 вес: 0+0-0=0
1->2 вес: 1+0-1=0
2->0 вес: -1+1-0=0
0->3 вес: 1+0-0=1
3->5 вес:0+0-1=-1 (Ребро с отрицательным весом)
Т.к. появилось ребро отрицательного веса, гарантий, что Дейкстра сработает нет. Я неправильно понял описанный по ссылке алгоритм, или он неверен?











В вершине 3 кратчайший путь — 1, а потенциал — 0. Нехорошо.
Т.е. обновляются потециалы всех достижимых вершин, а не только тех, по которым протолкнули поток?
Да.
Ясно, спасибо.
А где доказывается отсутствие отрицательных ребер?
d(v) — кратчайшее расстояние до вершины v.
e(u, v) — вес ребра из u в v.
Что конкретно у нас происходит? Был некоторый граф с потенциалами, мы посчитали на нем кратчайшие расстояния от истока до остальных вершин, затем добавились некоторые обратные ребра, и мы переделали потенциалы. У нас два вида ребер: те которые были изначально и новые обратные ребра. С теми, которые были в изначальном графе, все в порядке, для них воспользуемся правилом треугольника — d(u) + e(u, v) ≥ d(v) (иначе бы кратчайшие расстояния были бы некорректны, здесь еще следует сказать про отсутствие циклов отрицательного веса). Теперь рассмотрим новые ребра, они появились только на одном кратчайшем пути по которому протолкнули поток. Что верно для двух последовательных соседних вершин u и v кратчайшего пути? Что d(v) = d(u) + e(u, v). Если это не так, то найдется путь покороче или кратчайшие пути неверны. А какой будет вес обратного ребра для ребра (u, v)? d(v) + e(v, u) - d(u) = d(v) - e(u, v) - d(u) = d(u) + e(u, v) - e(u, v) - d(u) = 0. Ура, все ребра неотрицательного веса.
Еще раз спасибо!
Мне кажется, что в этом доказательстве ошибка:
Пусть у нас есть ребро
{a;b;w}({начальная вершина;конечная вершина;вес для Дейкстры}), по которому мы протолкнем поток.Обратное ему ребро будет иметь вид
{b;a;-p+d(b)-d(a)}, где p — цена единицы потока по{a;b;*}, умноженная на пропускную способность ребра{a;b;*}pне обязательно равноw, т.к. 'w' это цена + разность потенциалов.Т.е. вес обратного ребра будет равен
-p+d(b)-d(a)=-p+d(a)+w-d(a)=w-pНапример, пусть у нас будет такая остаточная сеть, 6 — исток, 7 сток:
Найдем в ней кратчайший путь
6->0->3->7длины 1 и протолкнем по нему 1 единицу потока.Исток и вершины 0,1,2 достижимы за 0. Все остальные вершины за 1.
Получим такую сеть: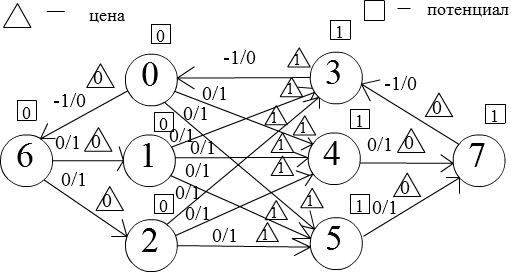
Все веса ребер теперь 0. Найдем кратчайший путь '6->1->4->7' и заменим все потенциалы на 0 (Т.к. за 0 можно дойти до любой вершины)
Получим такую сеть: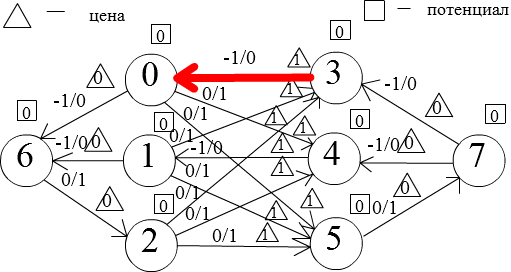
Ребро
3->0имеет вес -1+0-0=-1Во всех реализациях, которые я видел, d(v) добавляется к потенциалу вершины, а не присваивается в него.
Можно ли доказать, что при добавлении d(v) к потенциалу вершины после каждого выполнения Дейкстры в графе не появится отрицательных ребер, если их не было до этого?
Потому что те рёбра, которые вы развернули, будут иметь вес равный нулю.
Похоже, что да.
phi(x)— потенциал вершины x перед началом запуска Дейкстрыd(x)— кратчайшее по весам расстояние, найденное Дейкстройp(x,y)— стоимость единицы потока изxвyРассмотрим дугу
a->b, входящую в кратчайший путь. Ее весwравенphi(a)-phi(b)+p(a,b).По свойству кратчайших путей,
d(a)+w=d(b)=>d(b)=d(a)+phi(a)-phi(b)+p(a,b)Вес обратного ребра равен
d(b)+p(b,a)-d(a)+phi(b)-phi(a)=d(b)-p(a,b)-d(a)+phi(b)-phi(a)=d(a)+phi(a)-phi(b)+p(a,b)-p(a,b)-d(a)+phi(b)-phi(a)=0Для уже существующей дуги
a->bс весомwd(a)+w>=d(b)=>d(a)+w-d(b)>=0(Как выше доказал proVIDec)То, что в моем примере из предыдущего коммента вес уже существующего ребра становится отрицательным объясняется тем, что когда вместо добавления
d(x)кphi(x),d(x)присваивается вphi(x), значениеwменяетсяКаюсь. Свято верил, что когда-то доказывал оба варианта, поэтому написал быстро, не проверил. У меня даже задача есть, сданная не с прибавлением, а с присвоением :Р Сейчас сел порисовал, действительно несокращенная разность потенциалов остается, немного обманул. Хотя в приведенном источнике написано, что надо присваивать =)
Я в свое время писал mcmf только с дейкстрой без потенциалов, и все задачи нормально сдавались. А потом узнал, что в таком случае оно за экспоненциальноевремя работает на специально подобранных тестах и перестал так писать :)
Про потенциалы еще в Кормене вроде было, вроде где-то в задачах и под названием "Алгоритм Джонсона".