laoriu's blog

Codeforces Round #277(Div. 2) Editorial
By laoriu, 10 years ago, In English

486A - Calculating Function

If n is even, then the answer is n / 2, otherwise the answer is (n - 1) / 2 - n =  - (n + 1) / 2.

486B - OR in Matrix

Hint of this problem is presented in its statement. "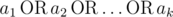 where 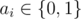is equal to 1 if some ai = 1, otherwise it is equal to 0."

To solve this problem, do 3 following steps:

  1. Assign all aij (1 ≤ i ≤ m, 1 ≤ j ≤ n) equals to 1.
  2. If some bij = 0, then do assignments: aik = atj = 0 (1 ≤ k ≤ n, 1 ≤ t ≤ m) (that means, assign all elements in row i and column j of matrix a to 0).
  3. Then we have matrix a which need to find. Just check whether from matrix a, can we produce matrix b. If not, the answer is obviously "NO".

Complexity: We can implement this algorithm in O(m * n), but it's not neccesary since 1 ≤ m, n ≤ 100.

486C - Palindrome Transformation

Assuming that cursor's position is in the first half of string(i.e 1 ≤ p ≤ n / 2) (if it's not, just reverse the string, and change p to n - p + 1, then the answer will not change).

It is not hard to see that, in optimal solution, we only need to move our cusor in the first half of the string only, and the number of "turn" is at most once.

Therefore, we have below algorithm:

  • Find the largest index r before p in the first half of the string (p ≤ r ≤ n / 2) such that sr different to sn - r + 1. (si denote ith character of our input string s)

  • Find the smallest index l after p (1 ≤ l ≤ p) such that sl different to sn - l + 1.

  • In optimal solution, we move our cusor from p to l and then from l to r, or move from p to r and then from r to l. While moving, we also change character of string simultaneously (if needed) (by press up/down arrow keys).

Be careful with some corner case(for example, does'nt exist such l or r discribed above).

Complexity: O(n).

486D - Valid Sets

  • Firstly, we solve the case d =  + ∞. In this case, we can forget all ai since they doesn't play a role anymore. Consider the tree is rooted at node 1. Let Fi be the number of valid sets contain node i and several other nodes in subtree of i ("several" here means 0 or more). We can easily calculate Fi through Fj where j is directed child node of i: 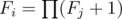. Complexity: O(n).

  • General case: d ≥ 0. For each node i, we count the number of valid sets contain node i and some other node j such that ai ≤ aj ≤ ai + d (that means, node i have the smallest value a in the set). How? Start DFS from node i, visit only nodes j such that ai ≤ aj ≤ ai + d. Then all nodes have visited form another tree. Just apply case d =  + ∞ for this new tree. We have to count n times, each time take O(n), so the overall complexity is O(n2). (Be craeful with duplicate counting)

Here is my code.

486E - LIS of Sequence

LIS = Longest increasing subsequence.

Solution 1 (Most of participant's solutions):

  • Let F1i be the length of LIS ending exactly at ai of sequence {a1, a2, ..., ai} and D1i is the number of such that LIS.
  • Let F2i be the length of LIS beginning exactly at ai of sequence {ai, ai + 1, ..., an} and D2i is the number of such that LIS.

  • // Calculates F1i and F2i is familiar task, so I will not dig into this. For those who have'nt known it yet, this link may be useful)

  • // We can calculate D1i and D2i by using advanced data structure, like BIT or Segment tree.

  • l = length of LIS of {a1, a2, ..., an} = max{F1i} = max{F2j}.

  • m = number of LIS of {a1, a2, ..., an} =

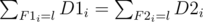
  • Let Ci be the number of LIS of {a1, a2, ..., an} that ai belongs to. Index i must in group:

    1) if Ci = 0

    2) if 0 ≤ Ci < m

    3) if Ci = m

  • How to calculate Ci? If (F1i + F2i - 1 < l) then Ci = 0, else Ci = D1i * D2i. Done!

We have an additional issue. The number of LIS of {a1, a2, ..., an} maybe very large! D1i, D2i and m maybe exceed 64-bits integer. Hence, we need to store D1i, D2i and m after modulo some integer number, call it p.

Usually, we will choose p is a prime, like 109 + 7 or 109 + 9. It's not hard to generate a test such that if you choose p = 109 + 7 or p = 109 + 9, your solution will lead to Wrong answer. But I have romeved such that tests, because the data tests is weak, even p is not a prime can pass all tests.

Solution 2:

// Some notation is re-defined.

  • Let F1i be the length of LIS ending exactly at ai of sequence {a1, a2, ..., ai}.

  • Let F2i be the length of LIS beginning exactly at ai of sequence {ai, ai + 1, ..., an}.

  • l = length of LIS of {a1, a2, ..., an} = max{F1i} = max{F2j}.

  • Let Fi be the length of LIS of sequence {a1, a2, ..., ai - 1, ai + 1, ..., an} (i.e the length of LIS of initial sequence a after removing element ai).

  • Index i must in group:

    1) if F1i + F2i - 1 < l, otherwise:

    2) if Fi = l

    3) if Fi = l - 1

  • How to caculate Fi? We have: Fi = max{F1u + F2v} among 1 ≤ u < i < v ≤ n such that au < av. From this formula, we can use Segment tree to calculate Fi. Due to limitation of my English, it is really hard to write exactly how. I will post my code soon.

Complexity of both above solution: O(nlogn).

  • Vote: I like it
  • +94
  • Vote: I do not like it

Comments Comments (70)
| Write comment?
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Really quick editorial! Thank you. The problems are very interesting :)

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it -27 Vote: I do not like it

    Are you talking about quick sort ? i think merge sort is faster .

    /* */

    it seems to be easy to prepare such a quick editorial for that easy problems.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      Yeah.It was so easy, so you solved 2 problems? Do not comment other's work if you are not able to do something like this.I can bet you won't host a codeforces round in your miserable life.

      → Reply
»
10 years ago, # |
  Vote: I like it +11 Vote: I do not like it

There're too many unrated contestant in the top, I think they come from Div1, that make my rank low :(

→ Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it +47 Vote: I do not like it

Here is one more solution for E. It looks like your first solution but is easier and deterministic.

First, calculate F1i and F2i for all i. Obviously, if F1i + F2i - 1 ≠ l than answer for i is 1, otherwise it is 2 or 3.

Then, assume there are two elements i and j with answer different from 1 such that F1i = F1j. You can prove that in this case you can replace i-th element with j-th one in any LIS containing i-th element. Thus the answer for i is 2 (and for j it is 2 too, of course). It can also be shown that if F1i is unique among all F1 then the answer for i is 3.

So the algorithm is the following:

  • if F1i + F2i - 1 ≠ l then the answer for i is 1
  • else if F1i is unique (among positions where we didn't assign 1 yet) then the answer for i is 3
  • otherwise the answer for i is 2
→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    What about this case: a = {1, 3, 4, 2} => F1 = {1, 2, 3, 2}. We have F2 = F4 (this is 1-based indexing), but in fact, the answer for index 2 is 3, the answer for index 4 is 2.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      If F1i + F2i - 1 ≠ l then we ignore this number in latter computations.

      And in your example the answer for index 4 is 1 because the only LIS is {1, 3, 4}.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +4 Vote: I do not like it

        Oh, I get it! What a great and simple solution! Thanks!

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it -31 Vote: I do not like it

        do you mean "computational geometry" with "latter computations" ?

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it +32 Vote: I do not like it

          Do you mean "a stupid joke" by posting stupid jokes?

          → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Such an elegant solution. :)

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    To check for 3-rd type we can construct first and last (lexicographically) sequences of maximum length and elements in intersection will have 3-rd type. They easy built from F1 and F2.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You have written "you can replace i-th element with j-th one in any LIS containing i-th element" but in case of [4, 5, 2, 3, 8] here f1[2] = f1[4] = f2[2] = f2[4] = 2 and f1[2]+f2[2]-1==3 but here we cant replace 5 with 3 in LIS [4 5 8] and neither 3 with 5 in [2 3 8]

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I didn't guess why we always can replace i-th element with j-th, but still I have an idea to show that if F1i = F1j then answer for i and j is 2. Let me write it here: suppose answer for i and j is 3, this means that they both participate in every LIS, now suppose ai < aj then this would mean that F1j = F1i + (# elements between them + 1) so these two values can't be equal. For ai > aj there is the same logic. I think I didn't got anything wrong here.

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Very simple and elegant solution. Thanks !

    → Reply
»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

waiting for D solution. :D

→ Reply
»
10 years ago, # |
  Vote: I like it +15 Vote: I do not like it

My solution for problem D. http://pastie.org/9712317

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Was your solution successful? I did the same stuff, it works fine on the samples, but fails on 5th test. Any ideas why could that be?

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    is it possible to do string matching with graphs?

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

2 things about problem B:

1) assign all elements in row i and column j of matrix a to 0, not to 1 (typo);

2) what is the n*m solution?

Despite this, thank you for a very interesting round:)

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    1) Thanks! Fixed!

    2) We can use additional array. For example: Ri = 0 means that we assign all elements of row i of matrix a to 0, otherwise Ri = 1; Cj = 0 means that we assign all elements of column j of matrix a to 0, otherwise Cj = 1. Then bij = Ri OR Cj.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    We can assign all elements in matrix A initially to 1.Then keep substituting the rows/columns of A where the same row/column in B has atleast 1 zero.This will create the A matrix and then check if it can form A. P.S.: I would also like to know the O(n*m) solution.

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    2) n*m solution can be done by simply keeping markers on which rows/columns you must mark with zeroes and then keeping track of which rows/columns are fully zeroed. However O(n*m*(n+m)) still works fine.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it -12 Vote: I do not like it

    do you mean "matrix exponantiation" with matrix ? if yes , press 8.

    → Reply
»
10 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Here's my deterministic and simple solution for E.

F1i + F2i -1 =/= l ===> the answer for i is 1

Now how to make difference between 2 and 3? Well if some i is of type 2, it means that removing it will leave some existing subsequence of length l. Let's find the elements in that optimal subsequence (after removal of Ai) that Ai lies between. Suppose those two are Ak and Ap, k<i<p.

If Ak<Ai<Ap then we could expand it, therefore this is false. So there is either Ak>=Ai or Ap<=Ai.

From this the following follows to be true:

If there is some Ak such that k<i, Ak>=Ai and (F1k+F2k-1)=l, then i is of type 2. Similarly, if there is some Ap such that p>i, Ap<=Ai and (F1p+F2p-1)=l, then i is of type 2.

Both can be checked in O(NlogN) with segment tree.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    for type 2 or 3 checking.

    Lets ignore all those "nodes" that never belong to the LIS. Use a map "ma" for counting the number of different nodes i that have F1i. that is:

    for(i = 0; i < n; i++){ if(res[i] == '1') continue; ma[f1[i]]++; }

    then, for every i check if ma[f1[i]] == 1. If it is true, every LIS in the array will have that node in the sequence at that level. Sorry about my english.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Very nice solution ! :D Also note that all the processes described by you can be done just using binary indexed trees. ( http://codeforces.net/contest/486/submission/8697188 )

    → Reply
»
10 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Editorials should have contain bit more details. Overall...thank you. :)

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

here is a solution for E without segment tree or BIT: 8657105

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Hi,

    Could you please explain how your solution works?

    I am unable to completely understand it but it looks nice.

    Thanks.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You can look at Exercise 15-4.6 in Cormen "Introduction to Algorithms" book.

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I did the same solution. I recommend use std::lower_bound\std::upper_bound to do a binary search over a sorted range. 8763721

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could you explain the main idea of the solution D, please?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem D I'm using the following logic :- I'm applying separate DFS on all the nodes, With the discovery of every node ( except the ones on which DFS had already been applied ) on whose addition the difference between minimum and maximum does not exceed 'D' , I'm adding 1 to the answer. Can anyone tell me why this logic wont work? Code :- 8665299

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    First, your min/max values change on different branches of the tree when you DFS. Second, you only count the number of nodes, while the statement asks for the number of sets.

    → Reply
»
10 years ago, # |
  Vote: I like it -25 Vote: I do not like it

Why Mr.Vuong makes this contest ?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Link to the code for problem D doesnt work

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

D — Valid Sets "Firstly, we solve the case d = 0. " It should be "d=inf"

→ Reply
»
10 years ago, # |
  Vote: I like it +7 Vote: I do not like it

I have another solution for E:

Let f[i] be the length of a LIS ending at a[i], and g[i] be the length of a LIS beginning at a[i], It's easy to see that L[i] = f[i] + g[i] — 1 is the length of a LIS containing a[i].

The length of LIS of A should be m = max{L[i]},

1/ An index i is belong to the 1st class iff L[i] < m

2/ An index i is belong to 2nd class iff L[i] = m and there exists ANOTHER index j so that (L[j] = m) and (f[j] = f[i]). Because a[i] and a[j] can never belong to the same LIS of A.

3/ The remaining index(es) will be assigned into 3rd class.

The computation of f[.] and g[.] takes O(n log n) time, and the classification takes O(n) times using counting technique

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can any anyone explain how is the following relation F(i)=prod(F(j)+1) true? where F(i) be the number of valid sets contain node i as root. F(j) is a node in subtree of i.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If we have only one child with F(j)=x for the root node, in how many ways can we make a tree containing root.(this is same as F(i) ). Surely x+1 as we can select child in x ways and not select in 1 way.

    When children increases we simply multiply F(j)+1 for every child we have.

    How to calculate F(j) for child? (Just do it recursively.) As we reach leaf node its F(i) will be 1.

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +9 Vote: I do not like it

    At each child j, you have the option to select (0,1,2....F(j)) valid sets from subtree rooted at j. Hence F(i) = prod(F(j)+1)

    It's the same as the proof of finding no of divisors of any number using prime factorization where,
    if n = a^x * b^y * c^z, no of divisors = (x+1)(y+1)(z+1). Proof
    Try to relate this to the no of divisors problem, you will find your answer :)

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      great explanation !!! thanks..

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you explain how we can avoid duplicate counting? Thanks.

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        While iterating on all nodes we suppose that the current node will be smallest in our subtree. Therefore for each node i we consider all other node j such that a[j]>=a[i] (and also a[j]<=a[i]+d) . Now suppose we are on j now than all the a[i]'s which are less will not be included in our answer but those a[i]'s which are equal to a[j] would have been already counted if (i<j) . So we check if (a[root]==a[v] && v<root) it means answer for node v has already been included.

        → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My solution for problem E. :) http://codeforces.net/contest/486/submission/8692548

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem E. S[i] is "length of LIS start exactly at i", E[i] is "length of LIS end exactly at i" If (S[i] + E[i] — 1 == l). A[i] belong to a LIS. Otherwise index i must in Group 1. I put A[i] in to n layer (L), n = max{S[i]} = max{E[i]}, without any member of Group 1. A[x] belong to L[i] if (S[x] == i) (or E[x] == i, anyway) If L[i] include 1 element, index of this element belong to Group 3, because we can't make a LIS without it. Otherwise, index of these element belong to Group 2.

I haven't code it yet but I think my solution more simple them 2 solution of laoriu, but if anything wrong, tell me pls :).

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I cant understand how to caculate Fi using segment tree? Can anyone tell me ?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I don't see any segment tree used in calculating Fi. You are referring to D-Valid Sets, right?

    We just used DFS to do our work.Can you give link to the solution which used it?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      i forgot it. segment tree is in E solution. in solution 2, laoriu says: "we can use Segment tree to calculate Fi" but how ?

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can you please tell me how one can think of solution to problem OR matrix in this(tutorial) way? I mean to say is there any specific algo related to it or its pure thinking skill.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

problem C is giving correct output(i.e. 6) for first test on my system,but codeforces is showing output '0' for same test.Plz help. http://codeforces.net/contest/486/submission/11666147

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone tell me how to solve problem E using the way mentioned in the editorial? I have already solved after reading ifsmirnov comment but I want to solve the problem with the way mentioned in the editorial because I am weak at segment trees , can someone explain or link their solution? thanks!

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Editorial to problem D is love.(^_^)

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can anyone please explain the equation of problem D? especially why we have add one to all f[v] before multiplying with f[u]?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hey Guys, Query regarding 486D- Valid Sets: considering case when d= inf, number of valid sets would differ based on root. Consider following case:

3 1 2 2 3 when we run dfs(1), number of valid sets will be 3 when we run dfs(2), number of valid sets will be 4.

Can anyone clarify this and explain the formula for calculating valid sets.

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

There's a mistake on tutorial of problem C. In the bullet point it says that r should come before but the equation (p ≤ r ≤ n / 2) says the opposite, so just swap the "before" and "after" in the bullets and happy AC :)

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain how to find the number of LIS ending at index i ?

( Finding D1,D2 in problem E of the editorial )

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

This is one of the best rounds I have ever upsolved! Wow! Kudos to the author.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you tell me the intuition of reducing duplicacy in the "D:valid sets" problem?

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Root the tree at vertex $$$1$$$.

      In my solution 103156285,

      $$$dp[v][x]$$$ stands for the number of subtrees, rooted at $$$v$$$, for which the MAXIMUM $$$=x$$$ and MINIMUM $$$\geq x-d$$$.

      $$$f[v][x]$$$ stands for the number of subtrees, rooted at $$$v$$$, for which the MAXIMUM $$$\leq x$$$ and MINIMUM $$$\geq x-d$$$.

      You can think of the transition yourself (or look into my code. It is not hard. It's just DP on trees.).

      Now the answer is obviously sum over all $$$x$$$ for every vertex $$$v$$$. You can see, that in this solution of mine, there is no problem of overcounting at all, since each $$$dp[v][x]$$$ denotes a sub-tree with either different root $$$v$$$ or different maximum value $$$x$$$.

      → Reply