Hello everyone! I have difficulties in solving the following problem (it's from a Romanian judge):
Given a directed acyclic graph with N nodes (1 < = N < = 100) and M edges (1 < = M < = 5000), find the minimal number of paths necessary to cover the graph (that means that each vertex is contained in at least one path). Paths are not necessarily disjoint, so a vertex or an edge can be part of multiple paths.
For example, for N = 7 and M = 7 and the following edges:
1 2
7 2
2 3
2 4
3 5
4 5
4 6
the answer is 2 (one path may be 1->2->3->5 and the other 7->2->4->6).
Thank you in advance!
Edit: Case solved, see mmaxio's indication and xennygrimmato's link.











Find the transitive closure and solve the problem for disjoint paths.
Could you also provide me a brief proof?
It's not hard to see how to transform a cover of G into a disjoint cover of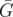 without changing its size(replacing paths with an edge), and vice versa.
without changing its size(replacing paths with an edge), and vice versa.
Thanks, it works indeed ^^
Can you please explain your approach a bit more? I'm having some difficulty understanding it.
Maybe this and this could help.
These help solving the problem after following mmaxio's indication. Thank you too!