490A - Командная олимпиада
Будем формировать команды жадно. То есть, если у нас есть по одному школьнику каждого из трёх типов, которые ещё не относятся ни к какой команде, то из них можно сформировать новую команду. И так делее, пока достигнется ситуация, когда мы не сможем сформировать команду. Таким образом, общее число команд — это минимум из количеcтва школьников каждого из трёх типов. Решение получается за O(N), если сложить индексы школьников каждого типа в три отдельных массива. Можно решать и за O(N2), если каждый раз пробегаться по всему массиву в поисках школьника конкретного типа для очередной команды.
490B - Очередь
Эту задачу будем решать конструктивно. Определим, кто находится на первом месте — это студент с таким номером, который встречается среди чисел ai, но не встречается среди чисел bi (потому, что ни для кого из остальных он не находится позади). Определим, кто находится на втором месте — это студент, который стоит позади первого, а поскольку у первого студента число ai равно 0, то соответствующее ему число bi и будет его номером (то есть число из пары [0, bi]).
Теперь будем определять остальных, начиная с третьего. Это делается очень просто по предпоследнему уже определенному номеру студента. Номер очередного студента, это число bi в некоторой паре, где число ai, это номер предпоследнего уже найденного номера студента (то есть число из пары [ans[i - 2], bi]. Решение достаточно просто осознать, разбирая пример из условия.
490C - Взлом шифра
Будем решать эту задачу следующим образом. Сначала проверим все префиксы заданного числа — делятся ли они на число a. Это можно сделать за O(N), где N — это длина заданного числа C. Зная остаток от деления префикса, заканчивающегося в позиции pos, можно пересчитать остаток для позиции pos + 1 следующим образом: rema[pos + 1] = (rema[pos] * 10 + C[pos + 1]) % a.
Затем нужно проверить все суффиксы числа C — делятся ли они на число b. Зная остаток от деления суффикса, начинающегося в позиции pos, можно пересчитать остаток для позиции pos - 1 следующим образом: remb[pos - 1] = (C[pos - 1] * P + remb[pos]) % b, где P — это 10^(L - 1) по модулю b, L — это длина суффикса (величину P можно вычислять параллельно).
Теперь нужно перебрать все позиции pos и проверить, можно ли сделать разрез числа C после этой позиции. Для этого необходимо выполнение четырех условий: префикс числа C, заканчивающийся в позиции pos, делится на число a; суффикс числа C, начинающийся в позиции pos + 1, делится на число b; длины префикса и суффикса ненулевые; суффикс не может начинаться с цифры 0. Если все эти условия выполняются, то после позиции pos можно сделать разрез. Если же все позиции не подходят, то решения не существует и следует вывести NO.
490D - Шоколадки
Заметим, что мы можем преобразовывать число следующим образом, либо делить на два либо делить на три и домножать на два. Изначально уберём из чисел все степени двоек и троек. После этого проверим, возможно ли удалив все эти степени добиться равенства площадей, если нет, то ответа не существует. Посмотрим на разность количества троек в факторизации шоколадок. Понятно, что именно на такое число нужно сократить одну из шоколадок, в зависимости от знака. Выполним данную операцию, пересчитывая количество двоек, и после сделаем то же самое для них.
490E - Восстановление возрастающей последовательности
Будем решать данную задачу жадным образом. Будем перебирать заданные числа сначала и пытаться сделать из текущего числа минимальное, но большее предыдущего. Обозначим текущее число — cur, а предыдущее число — prev.
Если длина числа cur меньше длины числа prev — следует вывести NO, задача не имеет решения.
Если длина числа cur больше длины числа prev — заменим все знаки ? в числе cur на цифру 0, за исключением случая, когда знак ? стоит в первой позиции — заменим его на цифру 1, так как числа в ответе не могут иметь лидирующих нулей.
Остался случай, когда длины чисел cur и prev равны. По условию задачи, каждое число в ответе должно быть строго больше предыдущего. Переберем позицию pos, в которой префикс числа cur больше чем префикс числа prev. Теперь попробуем для этой позиции сделать минимально возможное число, большее prev. Во всех позициях posi в которых стоит знак ? и меньших pos, поставим цифру, которая стоит в соответствующей позиции числа cur. А во всех позициях posi в которых стоит знак ? и больших pos, поставим цифру 0. Если в числе cur в позиции pos стоит знак ?, то поставим в эту позиции цифру на 1 большую, чем prev[pos]. Если в prev[pos] стоит цифра 9, то данная позиция pos не подходит для рассмотрения.
Если полученное число меньше либо равно предыдущему, то данная позиция pos не подходит. Из всех подходящих позиций pos выберем минимальное число, полученное в результате описанных выше действий, присвоим ему число cur и продолжим восстановление ответа. Если подходящих позиций pos на каком-то шаге не нашлось — следует вывести NO.
490F - Турне по Древляндии
Задача является обобщением нахождения наибольшей возрастающей подпоследовательности в массиве, поэтому наверняка решается диначеским программированием. Будем делать динамику d[(u, v)], в которой состоянием является ориентированное ребро в графе (u, v). В динамике будем хранить максимальное число вершин, где группа могла дать концерты на каком-то простом пути, заканчивающемся в вершине v и проходящем через вершину u. Причём в вершине v точно будет концерт.
Чтобы посчитать значение для ребра (u, v) нужно посчитать значение для всех рёбер (x, y) таких, что существует простой путь, начинающийся в вершине x, проходящий через вершины y и u и заканчивающийся в вершине v.Чтобы найти все рёбра (x, y), удовлетворяющие этому условию, нужно просто запустить обход в глубину из вершины u, которому будет запрещено заходить за вершину v. Тогда все ребра, которые он обойдёт, нужно просто взять с обратной ориентацией. Таким образом если r[y] < r[v], то d[(u, v)] = max(d[(u, v)], d[(x, y)] + 1). В итоге получется решение за O(N2) и (O(N2)) памяти. Память можно сократить до линейной если научиться получать индексы ориентированных рёбер без обращения к двумерному массиву.











comments soon
How to find a student which in first place in problem B?
You might use map-container. Every non-first and non-last student appears in the input twice. Just keep the map <Student ID, appearances> and traverse it at the end.
Thanks)
In problem E, case: lengths of number a and b are equal, if (cur[pos]=='?') then cur[pos] = max(prev[pos] + 1, 9) or cur[pos] = min(prev[pos] + 1, 9) ?
it can't be max(prev[pos] + 1, 9)
it should be min(prev[pos] + 1, 9)
i think it is a typing mistake
Will someone please explain approach to problem D : Cholocate ?
I am not able to get the explanation described...
Thanks
+1, the comment says: " Firstly remove all 2 and 3 from factorization of chocolate and determine equals their square or not.". This sentence makes no sense....
You can factorize the dimensions of the chocolate. Taking the second sample case, you have 36 × 5 and 10 × 16; the factorizations are 36 = 22·32, 5 = 5, 10 = 2·5, and 16 = 24.
Now you remove all factors of 2 and 3. Thus, 36 turns to 1, having all factors removed. 10 turns to 5, having the 2 removed but not the 5. 5 remains a 5.
After doing this, we are left with 1 × 5 and 5 × 1. The areas are equal (both are 5), so we can solve this (at least by cutting all chocolates by thirds, then by halves; we will always end up with 1 × 5 and 5 × 1 if we keep doing the cutting, although there might be a better solution). If the sizes aren't equal (such as in third sample case, where you have 1 × 5 = 5 and 1 × 1 = 1), you can't solve it.
I got wrong answer for test 12, but when I checked the results from jury's and my outputs, they are both correct, I mean number of minutes in both outputs are the same and aXb equals cXd where a,b,c,d are the sides of those chocolates. here is my code 11133391 and judge result http://postimg.org/image/4qmj8m90b/
Is there any faster solution for F than O(N2) ?
I can't follow all the logic, but this looks like O(N * logN) to me: 8816064
I'm not sure but I think it's O(N*(logN)^2). In each "MergeQuery" operation, it takes O(logN) for every node in tree2 to query and insert. By controling the size of t2 smaller than t1, it can be guaranteed that every node will be involved in a MergeQuery option for at most logN times. I think this upper bound can be reached in a full binary tree.
You are right, It's O(N*(log N)^2).
Hey I_love_Hoang_Yen, I implemented the
O(N^2 * logN)solution in Java similar to your submission but it gives me TLE. I'd appreciate it if you could take a look and point out if I'm doing something wrong: Treeland Java submissionHey! could you further explain D.chocolate more clearly? What do you mean by saying: "Firstly remove all 2 and 3 from factorization of chocolate and determine equals their square or not". Whose square equals who? Really appreciate it......
Well, I think it means you should check whether the products of the width and height after removing all 2 and 3 are the same. The "square" in the sentence seems weird to me though.
Thanks!!!I also guess so...lol
Is there any sample code of problem F using the idea in the tutorial? I can't understand how to implement this......
My submission (http://codeforces.net/contest/490/submission/8886626) is pretty much like that.
Things to be aware of: You have to add a dummy edge coming from (but not to) any leaf to a dummy node.
I also do not use DP, but rather memoization, that way I do not have to worry about the order in which I process the edges.
I got it, thank you very much!
My program on pretest 8 in question A, gives the wrong answer, but why? Please somebody help me. My program:(in Python 3)
Well, you use index I twice inside the try block... I'm pretty sure that changing the index to a unique name (for example, use "for J in range(N)" the first time and then "for K in range(N)") will lead to a correct answer in that test. Also, I think the algorithm will be too slow to pass all the tests. The condition in the while loop takes O(N) to evaluate, and then you make an O(N^2) loop inside.
No,Python it does. If two "for" at the same time to counter the "I" the two "I", by mistake do not move . My problem is that when all the students in the teams my program one fewer runs Anyway, thank you that you are trying to debug my program but my problem still remains ...
Oh, sorry for my ignorance :( Yesterday I made a submission based on your code, would you mind taking a look at it? 8849662 If I understood correctly, this solution passes the test you mentioned. If not, I apologize for my mistakes.
Thank you very much. I have no problem with my program & I think Time Limit Only in python codes(for this question)
No, you have TLE everywhere. O(N3) algorithm will not pass for N = 5000 even with C/C++ (two of the fastest languages on Codeforces). You need to rethink your algorithm.
No, it doesn't. True, the
Iin the outerfor(the one directly insidetry) will not be affected as it iterates alongrange(N), but theIoutside (the global variable) will be affected; when it exits thefor/forloop,Iwill be equal toN-1(being the last value in the inner list).Here is a modified version of your code, where I removed the output code and added a print statement for what value of
Iand in which loop the program is currently reading. As you can see, after breaking out from the innermost loop,Iretains its value, leading toglobal 5instead of the expectedglobal 1. (This also means1 1 2 2 3 3fails your program, as you only got the first1 2 3, not finding the second.)Oh, Yes! Your edit is best edit with my code. I'm a Python newbie programmer. Thank you for helping me.
Could anyone tell me what's wrong with my code for F? 8840730 I get TLE on test #53 and I'm not sure why :/
Thanks !
Your algorithm seems to be O(N3), when it should actually be O(N2) or a low constant factor O(N2 * logN).
Thanks! :) I think I get it, it's because I do the LIS search at the end of every path, so there are a lot of repetitive search.
I don't see why it is O(N3) though, I would think my solution is O(N2logN) which is why it doesn't pass as it is supposed to be O(N2). Am i wrong ?
O(N2logN) can pass easily, I think. My solution is O(N2logN) because of some unnecessary binary search, but it still pass in 124ms. I think your solution is O(N3logN) because you have to enumerate all the vertex in the tree as the root. Maybe there's a more accurate analysis though... Edit: My example is wrong, but I still think it's not O(N2logN).
I think you are right ! I believe my solution is O(N2 + PNlogN) where the O(N2) is for the dfs and the O(PNlogN) where P is the number of paths to search LIS can be up to N2 (let's say each node is match to all the other nodes) so effectively the total complexity is O(N3logN) which is too slow!
Thanks for the help !
I am unable to understand
D-Chocolate.All I can understand is iff you havea1*b1anda2*b2first remove all 2's and 3's from them and after removing ifa1*b1!=a2*b2then answer isNOelse we have to do something. Can anybody tell me what next we are supposed to do?The idea is to make the exponents in a1*b1 and a2*b2 equal.
Got that.Thnx :)
Is it possible to get full test-cases of Problem-E ? I am getting WA in test-case 9, but the test-case is truncated after some values. There are dots (...) which means continue, but the full test-cases are not there.
Is there anyway to get this I am missing?
Thanks.
Mistake is in lines 55-66 of your code. Your programm doesn't react if two numbers are equal
Test:
2
1
1
Thanks Kefaa!
My code had another major problem. After submitting 17 times I got Accepted!!! Yaaayyyy...!!! :D :D :D
After reading the tutorial, I realized how unnecessary this solution by me is: http://codeforces.net/contest/490/submission/8829276
в задаче B у меня программа работает за O(n*log(n)). Но на 47 тесте TLE. в чем проблема?
In D-Chocolate could any one explain that why does a solution exist after removing all 2's and 3's as factors ??
You can see the no. of segments in each chocolate bar, as factorized by 2 and 3: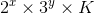 . the actions only change
. the actions only change
xandy, notK. So if two K do not equal, answer doesn't exist.Thnx, got it!!
well, i am a beginner....here in PRBLM A told to print any of the solution....for the first pre test why it is ans 3 5 2 and 7 6 4 why not 1 5 2 and 3 6 4....
Both of them are right answer for test 1 so you can output one of them.
Well,I'm not familiar to this website,I want to know where can I get the whole test data◔ ‸◔? I don't know why I'm wrong on test 7,and the test data on the website is not complete(..•˘_˘•..)
Here: http://codeforces.net/contest/490/submission/8895986
hello PROB : B http://codeforces.net/contest/490/my#
got TLE on test case 46 what can I do?
O(N * logN)
could anyone help me on how to solve Div2 Problem B using disjoint set data structure, as I found dsu tag attached with this problem.
I didn't understood the explanation for 490F so I went for browsing other's code instead, and here is a much more easier solution related to LIS with O(n^2 * log(n)) time complexity.
If you happen to be familiar with the LIS algorithm, you would understand that each time we visit a new node we just find the place where the new node could just fit into the optimal LIS, the only problem left is how do we choose the first position of the sequence and how do we handle a node leaving the LIS. (i.e. it has reached it's end in the euler tour)
So far I haven't come up with a brilliant answer with the first question, so it would be left as brute force from each node instead.
For the second question, keep a 2D-vector(or stack to be precise) to store the values, when a node leaves, just pop it from it's corresponding position and update the value from the updated top of the stack. This resets the LIS back to the state before visiting the subtree.
My implementation after viewing others ideas: http://codeforces.net/contest/490/submission/19867543
Hi haleyk100198 do you know why works when only calls the dfs from leaves?
If you are talking about my approach, it only works when it is called from the starting point of the journey.
haleyk100198 what's the complexity of your solution?
thanks!
"here is a much more easier solution related to LIS with O(n^2 * log(n)) time complexity."
Here, you are required to run O(n) dfs which takes O(n) time each, and the LIS algorithm inserts each node with a O(logn) time complexity.
in problem C why %b is done after multiplying with 10
i think that we need a proof :/
as we know number's length can be bigger than 10^6 so we have to make it smaller . ( to check %b) , so we go from rightmost number . keep in mind that in modular arithmetic we have properties :
(a+b)%c = (a%c + b%c) % c
(a*b)%c = ((a%c) * (b%c)) % c
suppose we have ...262 and b is 13 .
let's start from 62 we are interested in what is
(62)%13 . 62 = 6*10 + 2 ,
62 % 13 = (6*10 + 2) % 13 -> (6*10 % 13 + 2 % 13) % 13
then take 262
262 = (2*100 + 6*10 + 2),
262 % 13 = (2*100 %13 + 6*10 % 13 + 2 % 13) % 13 ,
we already know ( 6*10 % 13 + 2 % 13 ) % 13 so we take it from previous step , and we have to make 1 more thing , because our number 100 can get 10 ^ 6 , we have to make it smaller too , so we take (100%13) , then ((100%13)*10)%13 and so on ... i hope it helps :d