| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
I'm reading following tutorial: http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=hungarianAlgorithm
Description of O(n4) algorithm doesn't seem to be clear for me. Why do we need add 
to edges (v, w) where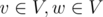 
? Why n2 iterations is enough, since we add weight to 0-edges?
It's pretty simple actually,
Consider you have the following matrix
As i'm sure you know this represents a bipartite graph of 5 + 5 = 10 nodes and 5*5 = 25 edges Next, find minimum vertex cover (i.e. min number of horizontal OR vertical lines such that we can cover all the zeros of the matrix (some elements might get covered twice)
Min vertex cover is 4. We need it to be 5 however so that we have a complete matching with edges only zero = minimum complete matching
We have to make one of the non-zero edges zero so that we can progress further. How do we do that? Recall that only transformations that are allowed are to add/subtract from a row/column so that the original matrix has the same solution as the transformed matrix
How do we subtract/add only from rows/columns so that our transformed matrix will have one extra zero edge? Here's the trick: we find the minimum edge not equal to zero (i.e. in our case a[1][3] = 2) and we subtract this value(i.e. 2) from all rows(i.e. left vertices) not in our minimum cover (in our example, rows in min cover are 2 and 4 => so rows not in min cover are 1,3,5)
So
becomes:
Here's the problem: we created negative edges from our zero edges! So solve this, we simply add 2 (i.e. our minimum which we found earlier) to all the columns in our vertex cover (in our example 2 and 5)
So
becomes
Now we can see that all our edges not having a vertex in the min vertex cover decreased by 2, all elements having only one vertex in the min vertex cover stayed the same, and, all the edges having both vertexes in min vertex cover increased by 2, which is equivalent to the formulas written on TopCoder.
Hope you understand now. Please tell me if something not clear. Cheers
I can't understand this excerpt: Min vertex cover is 4. We need it to be 5 however so that we have a complete matching with edges only zero = minimum complete matching I think mvc is 3 (3 horizontal lines)
You are right, my bad. I've modified a[5][5] from 6 to 0 and now it should be 4.
Thanks, I get it now .
If you can read in Russian, or may be google does it well from Russian to Polish, I would recommend to try e-maxx article. It describes Hungarian algorithm pretty well via duality of finding minimal permutation and maximal potentials. Also it has one of the shortest implementations (made by KOTEHOK) for O(n3) hungarian I've ever seen (also pretty fast, although I can make it faster).
Really helpful link, thank you. I used Google translate from Russian to English, and it works pretty decently — I am able to follow the article.
extremeplay has explained the process,yes,but why does the relation presented there works?I dont' get it.Proof or link to something which explains it on level above "My dad told me this works".I appreciate help.