Сегодняшняя дата напомнила мне об интересной задачке на spoj.pl.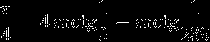
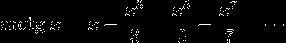
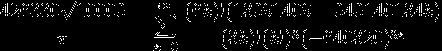

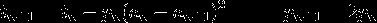
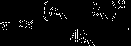
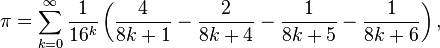
Все просто - нужно вывести как можно больше верных знаков числа Пи в десятичной записи за 25 секунд.
Я перепробовал множество методов:
от самых простых, (~200 знаков)
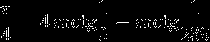
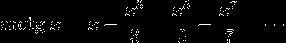
через забавные, (~1000 знаков)
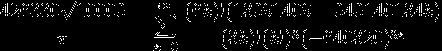
к наиболее эффективному из тех, что я пробовал (~7300 знаков)
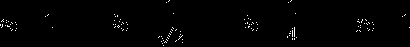

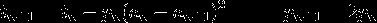
Витает еще идея использовать хитрую формулу
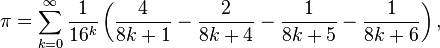
для получения шестнадцатиричной записи, и уже потом перевести что получится в десятичную.
Лучшее мое решение написано на яве с использованием BigDecimal и самописного квадратного корня.
Может оптимизировать длинку? Или искать другие методы, ведь есть же решения, выводящие 20002 знаков за 2.5 секунд?
Подскажите, как вычислить миллион знаков =)











Обычный алгоритм смены системы счисления (без быстрого умножения) работает за O(n^2)
На самом деле нормально написанное преобразование 20000 знаков в десятичную запись за O(n2) работает быстрее, чем за 0.1 секунды.
У меня на ноутбуке число из 66666 двоичных цифр переводится в число из 20069 десятичных цифр примерно за 40 миллисекунд.
Но это на C++.
Попробовал то же самое на Java. Работает 12-13 миллисекунд.
Перевод числа из 666666 двоичных цифр в число из 200687 десятичных на C++ проработал 4 секунды, а на Java 1.2 секунды (действительно O(n2) ^^).
Хмм. Некоторые программы, оказывается, можно ускорить, переписав их с C++ на Java. :)
Хотя, дело скорее всего в 64-битном компиляторе для Java.
Если скомпилировать код на C++ 64-битным компилятором под линуксом, то он работает 1.3 секунды.
У явы очень мощный JIT оптимизатор, но он помогает только если программа работает достаточно долго чтобы он успел сработать)
Подробностей не помню - давно решал подобную задачу. В той задаче нужно было вывести i-ю цифру двоичной записи π. Можно ли хитрую формулу эффективно распространить на много цифр - не знаю.
Вообще, при правильном использовании третья("забавная") формула позволяет считать миллионы знаков:
http://gmplib.org/pi-with-gmp.html
If you want to try a funny method for calculating Pi digits, I suggest you try some fixed point iterations:
x[0] = 3.14 (or anything close to Pi) and then:
x[i+1] = x[i] + sin(x[i]) -- cubic convergence (i.e. x[i+1] has ~3 times more exact digits than x[i]),
or better:
x[i+1] = x[i] + sin(x[i]) + 1/6*sin^3(x[i]) -- order 5 convergence
or perhaps even:
x[i+1] = x[i] + sin(x[i]) + 1/6*sin^3(x[i]) + 3/40*sin^5(x[i]) -- order 7 convergence.
An advantage of these methods is that they are 'fixed point iterations'. As a consequence, you don't actually need to be precisely accurate in your computations, because the iteration will converge to Pi for any decent approximation. So you should gradually (according to convergence order) increase arithmetic accuracy as the iteration proceeds.
Also notice that only one sin() has to be computed at each iteration, the rest is just a polynomial combination.
So the whole difficulty is now in calculating sin(x). Note that using some standard series around x=0 would be very inefficient, because x will be closer to Pi each time. A funny recursive method to calculate sin(x) is
sin(x, depth) = 3t-4t^3, where t=sin(x/3, depth-1)
sin(x, 0) = x
More depth - more accuracy. Also you could replace base condition by e.g.
sin(x,0) = x - 1/6*x^3,
or include even more terms, then you'll be able to use smaller depth. You'll need to find an optimal combination.
And start the next iteration from Ax (instead of x[n+2]).