Здравствуйте, уважаемые знатоки =)
Есть такая задача: дано N точек, N <= 2000; нужно найти трегульник максимальной площади, вершинами которого есть 3 и тех N точек. (Точки уже образуют выпуклый многоугольник и заданы в порядке обхода).
У меня 90/100 баллов.(Решал перебором вершины, а остальные две — двумя указателями).
Хотелось бы услышать советы и желательно код.
P.S.: идея у меня вроде правильная, но вот руки... =D
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
18:54:43
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
18:54:43
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 22:40:18 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Читаю заголовок — понимаю, что человеку интересно знать решение задачи или что-то уточнить. Читаю пост, и понимаю, что человек знает решение, да и к тому же рассказал его в посте. Дальше понимаю, что проблема в другом — в коде. А кода нет...
Так-то оно и есть)) Ищу человека, который писал подобное.
Ну ок. Но в посте просятся советы, дам один. Понятно как решать задачу за куб. И ошибиться там негде. Напиши стресс-тест.
Да у меня быдлокод, там что-то убери и все работать не будет :) Вот я и хочу чистую красивую реализацию увидеть. Этот метод(2 указателя) — вообще очень интересная тема.
N^2 * log(N) заходит?
Думаю, что да. Ты хочешь перебрать пару(вершини при основе), а потом тернарник запустить, чтоб 3-ую вершину найти(которая будет образовывать макс. высоту треугольника)?
да.
думал об этом... лень писать =D
Извиняюсь за оффтоп, но как вонимать вот это: 8568517, 8572637?
У меня был плохой день... =) Теперь я уже вырос и не делаю подобных вещей. Да и по правилам КФ ты не должен вылаживать свой код в интернет во время соренования(себя ты тоже спалил).
Интересно, куда же я его выложил?)
Интересно, откуда же я его взял?
Мне тоже это интересно)
pastebin.ru Ты выложил и не знаешь об этом? Может, ты сам его оттуда взял? =)
Боже, что ты несешь... Будь так добр предъявить пруф
И без пруфов понятно, что если у двух человек во время соревнования сдан одинаковый код — значит либо один дал свой код второму, либо им обоим дал код кто-то третий
либо первый выложил как public в ideone, а второй отловил
Может все-таки выкладывать?
Решение за квадрат. Совершенно очевидно, что все три точки лежат на выпуклой оболочке. Перебираем первую, вторую — в порядке обхода, два варианта третьей — указателями. Итого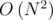
Возможно, здесь же есть решение за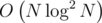
. Кажется, что вторую и третью точку можно подбирать тернарниками, если правильно разбить на отрезки (интуитивная оценка: расстояние до самой удаленной точки вдоль прямой выпукло относительно угла; площадь треугольника есть произведение двух таких расстояний и тоже выпукло; не проверял).
Можно решать за O(n), сделав вместо тернарников три указателя. Такая задача была в Петрозаводске года 4 назад.
Так ?
Именно.
Оно же не работает, правда?
Не работает