Give a sequence a[1], a[2], ..., a[n] (|a[i]| <= 15000, n <= 50000). Let function q(x, y) = max { sum(a[i]+a[i+1]+...+a[j]), x <= i <= j <= y }. There are m query form x y (1 <= x <= y <= n). (m <= 50000) calculate q(x, y)
Sorry for my bad English.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
Give a sequence a[1], a[2], ..., a[n] (|a[i]| <= 15000, n <= 50000). Let function q(x, y) = max { sum(a[i]+a[i+1]+...+a[j]), x <= i <= j <= y }. There are m query form x y (1 <= x <= y <= n). (m <= 50000) calculate q(x, y)
Sorry for my bad English.
| Name |
|---|



can you give problem's link ?
http://vn.spoj.com/problems/GSS/ Can you read Vietnamese?
There is an English version of it! :p SPOJ GSS1
Suppose for 2 given ranges (x, y) and (y+1, z) you know these things:
Maximum subarray starting at x and at y+1
Maximum subarray ending at y and at z.
Maximum subarray that lies completely within the intervals (x, y) and (y+1, z).
Total Sum of range (x, y) and (y+1, z).
Now, try calculating the same things for the range (x, z) using these 8 values.
Once you are done, you can make a segment tree storing these values to give you the answer.
Thanks
The solution to this problem is discussed here. The tutorial is written in Russian, use Google for translating.
You could find standard segment tree solution from lots of places, I would like to introduce a new solution under the constraints of this problem.
You can split queries into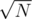 buckets by their x's. We will calculate answers for each of bucket separately.
buckets by their x's. We will calculate answers for each of bucket separately.
Sort all of the queries of current bucket by theirs end points. As you see starts point can change only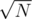 . End points are increasing, so you can calculate maximum sum interval lies between maximum start point and current end point. Also you can calculate max sum lies at left part with bruteforce O(N). One more thing, left optimal answer's start point can be at left part and endpoint at right part. This time one can just calculate maximum prefix sum of right part and minimum prefix sum of left part. Their difference equals maximum sum of last case.
. End points are increasing, so you can calculate maximum sum interval lies between maximum start point and current end point. Also you can calculate max sum lies at left part with bruteforce O(N). One more thing, left optimal answer's start point can be at left part and endpoint at right part. This time one can just calculate maximum prefix sum of right part and minimum prefix sum of left part. Their difference equals maximum sum of last case.
Overall complexity is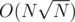
I will add some visual samples soon. Feel free to ask any questions.
Thanks, but the time limit is 0.09s...
It still has chance because constant factor is too little. I will implement it and share results if get accepted.
Firstly test set has huge inputs with M > 105.
Secondly time limit is not 0.09 seconds it is 0.23 seconds.
Fortunalty my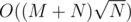 still gets AC with 0.19 secs which means 404th rank at best solutions list.(There are 5000 accepted solutions)
still gets AC with 0.19 secs which means 404th rank at best solutions list.(There are 5000 accepted solutions)
Here is the link to the implementation
I've solved it with segment tree. In each node you need to store the maximum sum starting with the leftmost element, the maximum sum starting with the rightmost element, the maximum sum of consecutive elements in the interval and the total sum. In my solution the variable indicator shows me if the total sum is equal to the maximum sum.
My solution
Ask if you didn't understand something.
Your code is great, thank you!