Всем привет!
Внезапно оказалось, что SnarkNews winter series — 2015 уже идет! Я вот чуть в очередной раз не пропустил серию.
UPD2: Первый раунд закончен, можно обсуждать задачи :)
UPD4, UPD: Второй раунд закончен, можно обсуждать задачи.
UPD3, UPD6: Третий раунд уже закончен.
UPD5, UPD7: Четвертый раунд закончился.
UPD8, UPD9: Пятый раунд уже закончился.
Спасибо snarknews за организацию соревнования.











Если я правильно понимаю, первый раунд уже завершился.
Расскажите как решать D.
Недавно на Codeshef была подобная задача. После раунда я погуглил и оказалось, что ответ равен N × (1 + 1 / 2 + ... + 1 / N)
Можно ссылку на задачу?
Player из December Cook-Off
Спасибо!
Там по ссылке:
Не родственник случайно?
Это фейк.
Помогите найти неправильную логику в рассуждении: Если не знать что задача баян, то можно посчитать МО по ее определению для дискретного случая:
MX = sum(x, p), гдеx— величина,p— ее вероятность. Тогда напишемdp[i][j]— вероятность того что мы наiбилетов соберемjпризов. При этом мы знаем чтоdp[0][0] = 1;p = 1 / n— вероятность приза в каждом билетеq = 1 - p— вероятность его отсутствияпереходы:
dp[i][0] = dp[i-1][0] * q;dp[i][j] = dp[i-1][j-1] * p + dp[i-1][j] * q; для j = 1..n-1dp[i][n] = dp[i-1][n-1] * p ;Что я упустил? PS: проблема в том, что такая логика даже для n = 2 дает ответ 4.0
Вроде бы здесь вместо p должна быть вероятность того, что мы найдем приз, которого еще не находили, то есть , ну и соответственно
, ну и соответственно  .
.
ага разобрались, спасибо.
С другой логикой получается проще. Когда вам нужно выиграть
Nпризов, вы берете один билет и с вероятностьюpвам остается выигратьN - 1приз, а с вероятностьюqвы опять пытаетесь выигратьNпризов. Матожидание работает по этой же логике и это дает возможность записать формулу мажидания:В первом уравнении переставляем члены, чтобы выразить
exp[N]черезexp[N-1],pиq.И, кстати, с помощью этой логики легко доказывается формула, данная выше
Кстати, а кто-нибудь решил В?
как С решать? Некоторые сдали С, но не сдали А(хотя А вроде намного легче). не классическая задача случайно?
dfs-ом можно посчитать для каждой вершины, какую выгоду нам принесут пути, начинающиеся в этой вершине и спускающиеся вниз. Из этих путей выбираем один или два самых выгодных и пытаемся обновить ответ. В предка возвращаем самый выгодный из путей.
Зафиксируем корень в дереве. Понятно что любой маршрут можно представить либо как путь строго вниз по дереву, либо как сначала вверх до какой-то вершины, а потом вниз.
Посчитаем динамикой по поддеревьям самый выгодный путь вниз для каждой вершины. Теперь осталось перебрать все вершины и найти самый выгодный маршрут (либо строго вниз от зафиксированной вершины, либо сначала вверх до зафиксированной вершины, а потом вниз).
Код
Объясните тогда и F кто-нибудь, пожалуйста :)
заведем массив cnt[10^5], cnt[i] — сколько было чисел i и массив mx[500], mx[i] — максимальное из чисел левее, делящихся на i.
теперь будем идти слева направо и поддерживать эти массивы.
пусти мы стоим в позиции idx и val == a[idx];
тогда если val <= 500, то возьмем ответ из mx[val], иначе пойдем семимильными шагами
for(int j = val; j <= 1e5; j += val) if(cnt[j] > 0) ans = max(ans, j);
теперь осталось обновить массивы. ну так и делаем cnt[val]++;
for(int i = 1; i <= 500; i++) if(val % i == 0) mx[i] = max(mx[i], val);
Можно завести массив множеств индексов sorted_sets[10^5], и для каждого элемента a[i] занести его индекс во все sorted_sets[d], где a[i] % d == 0.
Теперь для i-го элемента индексы кратного слева и справа хранятся в sorted_sets[a[i]], достаточно взять из него наибольший индекс, меньше i (или i, если такого нет), и наименьший индекс, больше i (или также i).
Такое решение работает за O(N * sqrt(maxA) + N * logN) с достаточно несложной реализацией.
Вроде как есть решение за NK, где K — максимальное число делителей чисел от 1 до 105. Изначально предпосчитаем все делители всех чисел за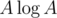 , где A = 105. Идем сначала слева направо и поддерживаем массив index[x], самое правое число делящееся на x. Пересчитывается это очень просто, пробегаемся по делителям текущего числа и обновляем массив. Аналогично пробегаем справа налево. Код.
, где A = 105. Идем сначала слева направо и поддерживаем массив index[x], самое правое число делящееся на x. Пересчитывается это очень просто, пробегаемся по делителям текущего числа и обновляем массив. Аналогично пробегаем справа налево. Код.
А сколько длится раунд? Правила TCM?
Раунд длится 1:20. Да, правила TCM/Time.
Спс
====Обсуждение задач второго раунда====Как решать F?
У меня возникло ощущение, что заходило любое работающее решение, там какие-то тесты в стиле американских полуфиналов или SWERC :)
У меня есть наивное решение за O(N2 * log(N)) — рассматривая запрос, подорвем все, что взрывается сразу; если от этого еще что-то сдетонирует — подорвем его; если от этого что-то еще сдетонирует — опять подорвем его... И так будем итерировать, пока что-нибудь взрывается.
Upd. С помощью sparse table из него даже можно сделать чистый квадрат :)
То ли у ребят с Яндекса весьма мощные сервера, то ли тесты ни о чем — в системе это решение работает за 1.3 секунды. При том что мое с контеста работает за 1.8 :)
Ну а локально у меня такой брут немного не укладывается в ТЛ — на одном худшем тесте из 100000 точек отработал за 1 час 51 минуту 55.167 секунд.
Шутки в сторону, вроде бы можно так:
За O(N * log(N)) сожмем все пути вправо; за O(N * log(N)) сожмем все пути влево. Теперь на запросы можно отвечать наивным итерированием, примерно так же, как и в описанном выше решении за квадрат. Так как теперь каждое расширение в запросе может быть только большим (перепрыгивающим через середину отрезка и расширяющим его с другой стороны), то всего их будет мало. Это должно дать нам что-то вроде O(N * log2(N)). Если дописать сюда update'ы полученными результатами и random_shuffle порядка запросов, то есть вероятность, что это работает даже лучше:)
P.S. Ну да, опять можно прикрутить sparse table — и убрать в начальной идее один логарифм.
Ну можно посчитать ответ за O( N logN + количество итераций ). Просто сохраним в SparseTable для каждой мины самый левый и самый правый индекс, куда дойдет взрыв, если он расширяется только влево и только вправо. Тогда расширить текущий интервал влево — взять минимум в первой структуре, а расширить вправо — взять максимум во второй и они выполняются за константу.
P.S. Слишком долго писал комментарий :)
Можно еще отсортировать мины по убыванию радиуса, тогда достаточно сделать одну итерацию и получается без sparse table.
без sparse table.
Нормальное решение можно почитать, например, здесь.
У меня больше вопрос по тому, почему это решение задачи D http://pastebin.com/grt4hxBL дает AC только на одном компиляторе (Oracle Java 7 x32), а на остальных TL. Что может быть не так? Не писать же кучу самому без классов.
кто-то обнулил время начала третьего раунда на yandex.contest :)
Как решать C из второго раунда?
Делаем ровно то, что написано в условии. Просят посчитать (A * B)N * N, значит посчитаем. Чтобы не было проблем с TL, запишем это как A * B * A * B * ... * A * B = A * (B * A)N * N - 1 * B, чтобы возводимая в степень матрица была маленькой; дальше быстрое возведение в степень, умножение матриц по определению и т.д. — сразу делаем все необходимые вычисления по модулю 6, в конце считаем ответ.
Спасибо snarknews за организацию соревнований, однако хочется указать на крайне низкое качество условий практически во всех раундах. Понятно, что принципиально новых и интересных задач никто не ждет, но плохо написанные условия с кучей неоднозначностей очень фрустрируют, тем более, что времени мало и на клары оперативно никто не может ответить.
Этот день настал — наконец-то мне на контесте пригодилось что-то из того, что проходят в университете. Впервые за последние полгода, как минимум. Это я о транспортной задаче в F из завершившегося час назад третьего тура:)
====Обсуждение задач третьего раунда====Как решать E?
В ней самое сложное — понять условие:) Организаторы хотят записать результаты бросков как число в k-ичной системе счисления, и поделить все возможные числа между N участниками поровну. Так как всего таких чисел ki, то нас спрашивают — при каком минимальном i число ki делится на N. Понятно, что если ki все еще не делится на N для какого-то достаточно большого i, то оно никогда не будет делиться, поэтому достаточно проверить первые несколько степеней. Вроде бы при таких ограничениях худший тест это 536870912 2, где ответ 29, но лучше перебирать с запасом.
Можно поймать минус на том, что для n=1 ответ всегда 0.
I_love_Tanya_Romanova, как ты это делаешь? Тебе пора делать скринкасты своих контестов!
Я не понял — это действительно кому-то интересно, или тебя заплюсовали за тонкий юмор? :)
На всякий случай — я записал скринкаст раунда 4. Регулярно это делать не планирую, я не Petr, не Egor и не tourist, и не (ставим сюда имя любого другого классного участника, для которого это имело бы смысл), но ведь один раз попробовать можно:) Пусть будет, если это кому-то интересно.
По понятным причинам, я не могу выложить сам скринкаст до окончания раунда. Если в Петрозаводске будет возможность — выложу оттуда. Иначе придется подождать еще несколько недель, пока я вернусь.
Upd. Спасибо добрым людям, которые мне только что объяснили — можно уже сейчас выложить на Youtube, а потом только снять ограничения конфиденциальности :)
Правда интересно. Сдать D с отметкой 00:00 (первый тур) — достаточно хороший результат, чтобы было интересно смотреть.
Я писал тот контест на Codechef в декабре, потом давал ссылку на статью в Википедии об этой задачи здесь на СF в обсуждении раунда, и еще обсуждал саму задачу и возможные решения с автором (Rubanenko) — после такого сложно ее не запомнить:)
Я уже залил видео, поставив ограниченный доступ; так что ждать несколько недель после окончания раунда — не придется, надеюсь)
Да не, я даже не про то, как закодить D за минуту, там и правда немного кода, вопрос скорее в том, а A, B и С уже были прочтены?
Как ты сам написал после просмотра видео — Вопрос, который я в топике задал, отпал.
Я уже опубликовал скринкаст, с него можно увидеть, что в подобных контестах я не считаю хорошей идеей тратить важное время сначала на внимательное и вдумчивое прочтение всех условий. Там ведь каждая потерянная минута в итоге умножится на 4-6 (в зависимости от успешности написания контеста).
Как решать F?
Не знаю, можно ли проще. У меня такое:
Воспользуемся тем наблюдением, что перед нами одна из модификаций транспортной задачи; только цены выброшены:) Очевидная часть — поскольку из параметров у нас только ограничения на пропускные способности, то существование решения можно проверить, пустив поток. В левую долю столбцы, в правую строки, клетки заменяем ребрами.
Теперь, видимо, менее очевидная часть — ведь нам еще нужно научиться проверять, единственное ли решение. Как мы знаем, все множество решений связно по перераспределениям, поэтому если мы нашли какое-то решение (потоком), то либо можно получить из него какое-то другое валидное решение, сделав одно перераспределение, либо же решение единственное.
Понятно, что перераспределять достаточно единичку. Если можно перераспределить больше, то можно перераспределить и единичку. Нам нужно найти цикл (по аналогии с любой вариацией метода потенциалов), по которому можно перебросить эту единицу. Это должна быть последовательность "делаем в клетке +1 — движемся по строке — делаем -1 — движемся по столбцу — делаем +1 — движемся по строке...", которая начинается и заканчивается в одной и той же клетке; либо же аналогичная последовательность, в которой + и — поменяли местами.
Наивно искать такую последовательность слишком долго. Но можно вспомнить, что каждому такому циклу отвечает цикл в двудольном графе из строк и столбцов. Предположим, что перед движением по строке у нас +, перед движением по столбцу -. Тогда у нас есть дуга из строки в столбец, если на их пересечении можно уменьшить число, и дуга из столбца в строку, если на их пересечении можно увеличить число. Теперь для проверки достаточно найти нетривиальный цикл в полученном двудольном графе. Так как в нем О(N * M) ребер, то с этим проблем не возникает. Ну и если бы нужно было показать, что решение не единственное, построив две различные валидные матрицы, то надо взять полученную потоком матрицу, и сделать в ней перераспределение по найденному нами циклу.
Вроде для проверки не единственности решения достаточно найти цикл в остаточном графе, это можно сделать дфсами также, как в поиске сильно связных компонент.
Непонятно, как. Цикл ребро-обратное ребро нам не подходит; нужен какой-то менее тривиальный цикл.
Да согласен, видимо нужно отдельно найти циклы на двусторонних ребрах, если нет, то сжать в компоненты связности, а потом поискать уже циклы на односторонних
Минусуют, потому что это неверно?
Уникальность можно проверить вот так:
Оно вроде не работает на тесте
fixedRow = fixedCol = 0, а единственным решением есть
Расскажите A.
Если доска из 4 строк:
Белые выигрывают, если суммарное количество единичных ходов нечетно, либо если количество столбцов, где доступны двойные ходы, нечетно.
Если строк не 4:
Решение — жадная стратегия. Столбцы, где только ты можешь сделать двойной ход — "хорошие". Столбцы, где только противник может сделать двойной ход — "плохие". Столбцы, где оба могут сделать двойной ход — "бесполезные". Во всех остальных столбцах достаточно знать только четность суммарного количества ходов.
"Бесполезные" столбцы выбрасываем. В них не имеет смысл ходить, пока есть другие ходы, потому что любой ход в нем создал бы "плохой" столбец (кроме случая с 5 строками и двойного хода, но такой ход тоже не имеет смысла). Если остались только "бесполезные" столбцы, то тот игрок, чей сейчас ход, проиграл. Это эквивалентно отсутствию "бесполезных" столбцов.
Далее совершаем ходы каждым игроком по очереди согласно такой стратегии:
1. Хорошо бы избавиться от "плохих" столбцов. Если такой есть, походим там, если их несколько, походим в том, где расстояние между пешками минимально.
2. Если плохих столбцов нет, но есть хотя бы один хороший, то мы делаем победный ход в нем. А именно, такой, чтобы суммарное количество единичных ходов стало четным.
3. Если нет ни "хороших", ни "плохих" столбцов, то победитель определяется по четности количества оставшихся ходов.
Почему не работает следующее "решение"? Подсчитать для каждой игры на одном столбце значения Шпага-Гранди (по определению). Сравнить xor Шпага-Гранди значений для всех столбцов с нулем.
Складывать игры можно, когда оба игрока имеют возможность делать одинаковое множество ходов из позиции. У нас, все же, это не так. Черный игрок не может двигать белые пешки, и наоборот.
Так можно было бы, если бы в фиксированном столбце обе пешки всегда имели одно и то же множество допустимых ходов. Но когда одна из пешек стоит с краю, а другая нет — это не так.
Да, спасибо, понял. Я почему-то подумал, что если отражать столбец симметрично после каждого хода (например, из (i,j) переходить в (n — 1 — j, n — 1 — (i + 1)), то такой проблемы не возникнет.
Удачная мысль рассмотреть отлеьно случай с 4мя строками. Я его отдельно не рассматривал и в итоге потратил на эту задачу кучу времени, тк там получается сложнее решение.
4 раунд вроде закончился, как делать C за 7 минут и D?
C:
Пусть координаты введены так, что все прямые параллельны оси OY. Если фиксирован угол, под которым упадет тарелка, то искомая вероятность – ее ширина (назовем это диаметром при данном угле) в проекции на ось OY, деленная на D.
Ну чудно, отсюда уже следует нормальное решение – можно вращать многоугольник, поддерживая диаметр, ответ – матожидание диаметра, деленное на D.
Правда за 7 минут вряд ли пишется. Зато пишется "возьмем 20 000 углов, найдем диаметр при многоугольнике, повернутом на этот угол, добавим к ответу". Заходит.
Да, вот то, что там точность 10 - 4, я как-то упустил. Последнее описанное решение очень простое и пишется тоже быстро.
По С я писал как раз последнее) Оно вроде бы очевидно с учетом требований к точности; да еще вспоминается задача D с последнего NEERC.
Там в ширина, деленная на D формально нужно еще сверху ограничить единицей — нас спрашивают о вероятности пересечения, а не о матожидании числа пересечений. Как ниже написали, в ней тесты такие, что можно ничего не ограничивать:)
В C как обычно хорошие тесты и заходит периметр выпуклой оболочки делить на π D , как нормально за 7 минут написать мне тоже интересно.
А что так не там с тестами? Периметр оболочки / π D — очевидно правильное решение (диаметр проекции = 2 * сумма проекций сторон, матожидание линейно, а матожидание проекции одной стороны — её длина / 2π D). Впрочем, я до этого не догадался и написал численное интегрирование по углу (писать там нечего, как и в решении с выпуклой оболочкой).
Это число бывает больше единицы например
А, ну да, я сказал не подумав, это верно только если диаметр многоугольника меньше d. Если там все тесты такие — это довольно странно.
Как минимум в задаче A тесты тоже так себе, у меня полная ересь зашла
Как-то так
В D с точки зрения тестов тоже дела обстоят не очень. У меня зашло такое решение (писал уже в самом конце, придумать ничего лучше не успел):
Интуитивно кажется, что нам бы в идеале иметь цепочку чисел типа 1, 2, 3, ... как в первом примере, тогда мы сможем их все собрать и получить N очков. Соответственно первым шагом я перевел каждого монстра в ближайшее к его здоровью незанятое число, меньше чем само здоровье. Т.е. например массив 1, 2, 3, 6, 6 превращается в 1, 2, 3, 5, 6. Некоторые числа могут при этом превратиться в 0, их можно выкинуть сразу. Дальше для каждого оставшегося числа считал сколько понадобится ходов, чтобы "собрать" это число и получить за него очко. Это значение для числа равно 1 + (на сколько мы уменьшили число на прошлом шаге). Получаем значения стоимостей каждого возможного балла. Плюс добавляем ограничение для каждой стоимости, что мы можем ее собрать только в течение первых h ходов, где h — изначальное здоровье монстра, в противном случае этого монстра убьет волшебник. Получились пары значений (стоимость в ходах)-(максимальный ход, к которому надо успеть эти ходы сделать). Эти пары пихаем в подобие рюкзака, это дает ответ.
Я сам очень удивился, что это зашло, потому что ни подумать, ни проверить никак не успел. После контеста мне написал I_love_Tanya_Romanova и сказал, что у него похожее решение и она неправильное, его сокомандник показал контрпример. Это решение не учитывает, что нельзя пропускать ходы и на тесте:
2 2 3
Наши решения выдают 2, хотя из-за того, что первый ход пропустить нельзя, 2 набрать не получится.
У меня есть мысль, что это решение можно допилить, чтобы оно проверило такой случае и все-таки выдало правильный ответ, но по факту у нас зашли неправильные решения. Я не знаю, есть ли подобный тест в тестах контеста, было бы интересно узнать, не на нем ли остальные участники получали WA.
Не умею доказывать строго, но кажется разумным такое жадное решение:
Моделируем каждый ход
1) если можем взять 1, то берем
2) разделим все различные значения, которые сейчас есть на цепочки отличающихся на 1 (1,2,3,5,7,8 разделятся на три цепочки 123+5+78). Смотрим на те цепочки, в которых есть значение, которое встречается несколько раз, выбираем из этих значений наименьшее в цепочке. Среди всех таких значений оставляем те, которые можем успеть довести вниз по его цепочке до того, как маг доберется до ее начала(с учетом того, что нам надо будет потратить часть ходов на убийство всех разных значений меньших данного), и берем минимальное из них.
Если я правильно понял решение, то оно не будет работать на таком тесте:
11
6 7 8 9 9 11 11 13 13 15 15
Твое решение будет уменьшать девятку, и в итоге останется без двух — 11 и 15.
Можно же уменьшить 11, 13 и 15 и собрать все, кроме 9.
Решение для случая, когда ходы пропускать можно было бы — вроде бы понятное, это выглядит как более-менее стандартная задача. Стеком раскладываем числа по ходам (правильность этого можно интуитивно доказать, попробовав поменять пару назначений в такой раскладке — от этого не может стать лучше, но может стать хуже), дальше рюкзак — мы помним, сколько у нас осталось свободных дней, и можем либо пропустить текущий день и получить +1 свободный день, либо же взять предмет, который назначен на этот день, использовав для этого предыдущие свободные дни.
Если я правильно понял слова Олега Христенко, то история примерно такая. В оригинальном условии задачи не было приписки о том, что ходы пропускать нельзя, но и явного акцента на том, что их можно пропускать — тоже не было. В версии для SNWS этого предложения сначала тоже не было, потом один из участников написал клар, для проверки запустили авторское решение, составив аналогичный указанному тест; оно для такого теста выведет 1, отсюда было принято решение о том, что ходы пропускать действительно нельзя. Оригинальные тесты проходят оба понимания условия.
Я сильно подозреваю, что подобный клар в изначальном контесте тоже приходил, после чего авторы "почистили" набор тестов таким образом, чтобы проходили оба понимания. Вполне распространённое судейское решение в случае, когда клар приходит в конце контеста.
С пропуском ходов есть такой момент — если пропускать ходы может и маг, то в некоторых случаях игра просто не закончится. То есть для разрешения пропуска ходов необходимо, чтобы в условии было явно прописано, что воин может стрелять ещё и в воздух (в то время как заклинание мага действует всегда). Ничего подобного в условии не было (и авторское решение написано в понимании, что ходы пропускать не получается).
Информацию, что проходит и второе понимание, я получил уже после того, как в таблице появился как минимум один плюc, так что добавлять "отсекающие" тесты уже возможности не было.
А можно тогда посмотреть на авторское решение, раз никто в таком понимании не умеет решать?
Расскажите как решалась B из четвёртого.
Правильно прочитать условие. Ключевая фраза — "остался без единой монеты". Т.е. у него в начале нет денег и в минус он уходить не может. Значит надо жадно посещать города в порядке возрастания b[i], если они не ухудшают баланс
Понял. Спасибо.
Вроде закончилось, расскажите как решать F из 5-го раунда, и можно ли C решить без бинпоиска?
И ещё задачу А.
Делаем бинпоиск по ответу, считаем сколько "плохих" экспедиций должно не попасть в s самых больших, на них используем минимальные карточки; на "хорошие" используем максимальные и проверяем, что минимальная из хороших получилась не меньше максимальной из плохих. В обоих случаях к минимальной экспедиции добавляем максимальную карточку, как-то так.
C без бинпоиска вроде можно, там же ограничение на координаты (и на ответ соответственно) — 105, так что можно просто таскать квадрат по всем сторонам и при возможности увеличивать его размер на единичку. Главное по каждой новой стороне тащить квадрат размера, на котором остановились в прошлый раз. Тогда независимо от того, как вы будете обходить стороны, квадрат не увеличится больше 105 раз. Но с бинпоиском вроде должно быть проще.
Я в дорешивании сдал такое решение: делаем динамику, внутри перебираем сколько мы пропихаем путей в текущего сына i и сколько из этих i путей уже существует j. Остальные пути мы должны создать. Это конечно TL, но оказывается что j достаточно перебирать до 2. Получается куб.
Тем временем savinov показал, что для попадания в топ3 достаточно написать только 3 раунда из 5:) Мои поздравления :)
Извените за оффтоп. Тур опенкапа завтра с 10 по Киеву? А то просто нас координатор проинформировал что тур с 11( И может быть жесткий конфуз.
Как решать B из 5-го раунда?
Возможно, есть более простые/приятные решения, но можно так, с помощью дерева отрезков:
Построим дерево отрезков по числам, которое будет знать, сколько сейчас вхождений каждого числа в последовательность. Теперь достаточно заметить, что запрос дублирования на сколько-то увеличивает число вхождений крайних чисел, а для всех внутренних (таких, все вхождения которых покрыты этим запросом) соответствует умножению числа вхождений на 2. Запрос максимума, в свою очередь, можно разбить на аккуратное рассмотрение краев (чисел, которые частично покрыты запросом) и запрос к дереву отрезков на максимум по полностью покрытым числам.
Идейно более-менее просто и понятно, но не знаю, насколько лаконично и красиво можно это реализовать. Еще нужно не забыть о случае, когда левая и правая граница запроса в пределах вхождений одного числа.
Я так и думал, но смущает, что там длинные числа нужно хранить в ДО. Такое проходит по времени?
Длинные числа — это long long?
Почему оно не должно проходить по времени? У нас n*log(n), константа не слишком большая, ТЛ целых 5 секунд, ограничения всего 50 тысяч, в мультитесте вряд ли все тесты большие.
Для проверки только что написал это, совсем втупую работает за 1.25. С long long везде-везде, с cin-cout, с лишними пушами и т.д.. Рискну предположить, что если переписать это нормально, то можно ускорить еще в 2 раза:)
Вот код.
Я вероятно где-то очень сильно туплю, но представим себе тест такого вида:
1) Сначала 49999 раз идет запрос на удвоение всего массива.
2) Потом 1 раз идет запрос на вывод максимума.
Разве в таком случае ответ — не длинное число? Разве в таких случаях границы инпута — не длинные числа?
r - l ≤ 108, поэтому после каждого запроса появится не более 108 "новых" чисел :)
Блин, я думал это только для второго типа запросов.