Привет
Некоторое время назад я наткнулся на персистентные структуры данных и, в частности, на описание персистентной очереди на вики-конспектах ИТМО. Всё бы хорошо, только как-то сложновато: чтобы реализовать одну маленькую очередь используется пять (в другом варианте — шесть) стеков.
Кратно напомню историю проблемы, уложусь всего в четыре стека и заодно немного расскажу про персистентность вообще .
Персистентность
Персистентность для структуры данных — возможность хранить несколько версий сразу. Другими словами, каждая изменяющая операция (например, у структуры данных «стек» есть операции push и pop) не меняет саму структуру, а возвращает новую стуктуру данных (обычно в виде ссылки на новую версию), в которой хранится то, что должно было появиться в старой после этой операции. Это эквивалентно тому, что можно (быстро) скопировать структуру данных целиком, а потом уже выполнять всякие операции.
Одна из самых простых для персистенизации структур данных — это вышеупомянутый стек. Персистентый стек — это дерево, в котором в каждой вершине хранится элемент данных и ссылка на следующий (в сторону корня). Версия стека — просто ссылка на одну из вершин. Корень дерева соответствует пустому стеку. Удаление из стека — это переход к следующей вершине по ссылке, добавление — подвешивание новой вершины.
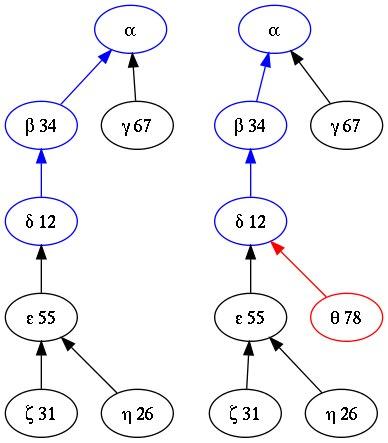
На рисунке показан пример персистентного стека до и после операции θ = push (δ, 78). Греческими буквами обозначены версии стека, например, версии η соответствует стек с элементами 34, 12, 55, 26, а α — пустой стек. В процессе работы со стеком могут появляться новые вершины, но старые не будут ни исчезать, ни изменяться, в этом и есть смысл персистентности.
Аналогичным образом можно персистенизировать и другие структуры данных, которые представляются в виде небольших структурок с ациклическими связями: двоичные деревья, дерево отрезков в варианте реализации сверху вниз. В случае двоичных деревьев обычно при запросе появляется не одна новая вершина, а сразу несколько, потому что надо создать новые версии для вершин, которые были затронуты и для тех, у которых были затронуты какие-либо потомки.
Ловкость лап и дерево отрезков позволяют придумать структуру данных «персистентный массив» с операциями «увеличить длину массива на один» и «изменить элемент», однако каждая такая операция будет выполняться за O(log) (логарифм длины массива). Поскольку любую структуру данных можно представить как изменение каких-то значений на массиве, то казалось бы, любую структуру данных можно персистенизировать с добавлением лишнего O(log) в асимптотике. Однако не всё так просто (впрочем, это позволяет из очереди на массиве сделать персистеную очередь с O(log) на операцию).
Персистентная очередь
Как известно, очередь легко реализовать с помощью двух стеков: из одного забираем элементы, в другой кладём, при необходимости берём и перекидываем все элементы из второго в первый. Заменив оба стека на персистентные получается персистентная очередь, так зачем в статье на вики-конспектах сложности с шестью стеками? Дело в том, что можно реализовать очередь через два стека, это даст оценку O(1) на операцию, но эта оценка — амортизированная. А персистенизация, к сожалению, не сохраняет амортизированные оценки.
Действительно, пусть у очереди версии ξ первый стек был пуст, и при следующей операции get (здесь и далее я буду называть операцию «положить элемент в очередь» как put, «взять из очереди» — get) придётся перекидывать элементы за O(n), где n — количество этих элементов. В обычной очереди эта операция бы выполнилась, и следующие n операций get будут выполняться легко и непринуждённо за чистую единицу. Но в персистентном случае от очереди могут потребовать что-то ещё сделать сделать с сохранённой версией ξ — и каждая такая операция будет выполняться за O(n). Неуспех.
Собственно, нагромождения с пятью–шестью стеками и нужны чтобы построить очередь, которая с одной стороны основана на стеках, с другой — выполняет операции за истинную O(1), а не за амортизированную, то есть пытается перекидывать элементы из второго стека в первый заранее, по одному, через несколько вспомогательных. Такая очередь уже легко персистенизируется. Но я начал с того, что пять (тем более шесть) стеков — это сложновато и сейчас попробую обойтись четырьмя.
Четыре стека
Первый стек ( main ) будет хранить просто все элементы, которые когда-либо добавлялись в очередь. Операция put будет добавлять элемент в main (а потом пересчитывать какие-нибудь счётчики и делать нечто).
Второй стек ( help ) будет хранить некоторые актульные элементы в обратном порядке, так чтобы из него всегда можно было брать элементы для операции get. То есть, операция get будет брать элемент из help (и тоже пересчитывать и делать нечто).
Чтобы не случилось так, что элементы брать неоткуда, нужен ещё один стек ( help2 ). В нём будут некоторые элементы очереди, он будет расти и когда help закончится (или раньше) придёт на замену.
Чтобы выращивать стек help2 нужна (внимание) персистентная копия стека main, из которой мы будет брать элементы и перекидывать элементы в help2. Эта копия у меня называется main2.
Выглядит это всё примерно так:
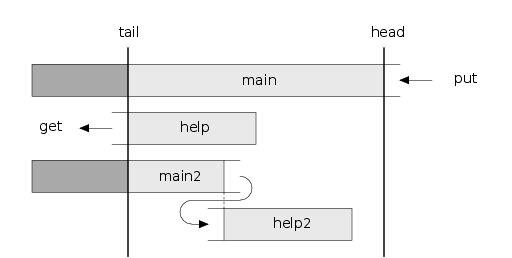
Действие, которое я назвал нечто — это и есть насыщение стека help2 и именно для этого надо хранить пару счётчиков. Достаточно знать количество элементов в очереди (пусть будет называться main_size, хотя на самом деле в main хранятся ещё и устаревшие элементы) и количество элементов, которые осталось перекинуть во вспомогательный стек (соответственно, main2_size). Операция put делает main_size++ и не трогает main2_size, операция get делает main_size--, main2_size--.
Ну а нечто стало быть должно делать следующее:
Если
main2_size > 0, то переместить один элемент из main2 в help2 иmain2_size--Если
main2_size == 0, то заменить help на help2, а help2 и main2 заменить на пустые стекиЕсли help2 пуст, то скопировать main в main2 (за
O(1), персистентный стек это как нельзя кстати поддерживает) и проставитьmain2_size = main_size.
Ещё следует доказать, что не будет ситуации, когда очередь не пуста, а стек help пуст, но я оставлю это читателю. У себя ВКонтакте я выкладывал код, который у меня получился на эту тему.
Минусы
Я знаю два минуса такой реализации по сравнению с пятью стеками, которые есть на вики-конспектах. Оба они возникли из-за того, что в стеке main хранятся вообще все элементы, которые добавляли в очередь, а не только те, которые остались в очереди на текущий момент.
Первый минус — это использование памяти. Если извне есть информация, что использовать надо не все версии, а только какие-то конкретные, то можно собирать мусор и экономить память. У меня же старые элементы так и будут висеть в хвосте main.
Второй минус заключается в том, что сложнее прикрутить какую-нибудь дополнительную возможность, например, подсчёт минимума на текущих элементах очереди. Это возможно, но понадобится ещё парочка вспомогательных стеков.
P.S. Слова «персистенизация» вроде бы нет в русском языке, так что мне самому интересно, как ещё можно назвать «построение по структуре данных её персистентного варианта».











Осторожно, необходимость упорядочивать греческие буквы может отпугнуть начинающих. (С другой стороны, что начинающим делать в статье про персистентную очередь?)
Эм, но их же не нужно упорядочивать, они уже.
А нельзя с двумя стеками сделать какой-нибудь рандомизированный вариант? Кажется, что достаточно ушаманить проблему с постоянным запросом при пустом первом стеке.
Удачи. Если ушаманится, то я с удовольствием почитаю, как именно.
Если не ставить цели чистить память, то вроде гораздо проще хранить такое же дерево, как в стеке + помнить для каждой версии сколько в ней элементов (для того чтобы удалять)
Не очень понятно, как сделать операцию get. Разве что двоичным подъёмом по дереву, это будет работать, но за
O(log)на операцию.Упс, и правда, наврал.
/
Недавно была похожая статья на хабре, если кому интересно — http://habrahabr.ru/post/241231/
Неплохо. Как я понял, такой же по сути подход, как и у меня, но взгляд с другой стороны.