Hello everybody,
Some weeks ago I started arranging contests very often in lightoj for me and some of my friends in order to practice. The problems are from lightoj's problemset. You can see the past contests here. Feel free to participate.
I can solve some of the problems but also there are some that I am not able to solve during the contest. After a contest I try to solve the problems that I failed. But I am not able to come up with solutions for all of them. There are three of the problems that I can't solve and find them very interesting:
Initially there is an undirected tree with N<=20000 nodes but then for some reason the edges become directed. We have to add minimum number of special paths so each node can be reached from each other. A special path is a chain of edges where each edge goes in the opposite direction of the edge in the initial graph. Special paths can share nodes and edges as well.
There are T<=30 test cases.
TL: 2s
ML: 32MB
My idea:
If I see an edge (a,b) I mark in[b] and out[a]. Then I am using dp[node] to calculate the answer. If out[node] is false then dp[node]=1. Otherwise dp[node] is the sum of the dp's of each node's children. Then I print the sum of the dp's of those nodes with in[node]=false.
Unfortunately, my idea is wrong because it fails this case:
5
0 2
1 2
2 3
2 4
The correct answer is 2, my solution prints 4.
2) Coin change 2 Solved! Thanks tenshi_kanade and ffao!!!
In a strange shop there are n types of coins of value A1, A2 ... An. You have to find the number of ways you can make K using the coins. You can use any coin at most K times.
N<=100
K<=10000
Ai<=500
All Ai will be distinct.
There are T<=100 test cases.
TL: 1s
ML: 32MB
My idea:
I use dp[current coin][current K] and calculate each state in O(K) which makes O(T*N*(K^2)) total complexity and gives TLE.
3) Dice 1 Solved! Thanks please_delete_account!!!
You have N dices; each of them has K faces numbered from 1 to K. Now you have arranged the N dices in a line. You can rotate/flip any dice if you want. How many ways you can set the top faces such that the summation of all the top faces equals S?
N<=1000
K<=1000
S<=15000
TL: 2s
ML: 32MB
There are T<=25 test cases.
My idea:
I use dp[current dice][current S] and calculate each state in O(K) which gives TLE.
Please, help me to solve them.
Thanks in advance!











Problem 1 can be solved much easier: the answer will be ceiling(L/ 2), where L is the number of leaves.
Just to prevent some possible arguments: a free vertex is not a leaf.
What about this case:
3
0 1
0 2
There are two leaves -> L/2=1
But the correct answer is 2.
Oh no, I didn't understand the meaning of the "chain of edges" phrase.
I'm sorry if something is not explained well.
In this image the black edges are the initial edges and there are two chains.
In the third problem you can use the idea of dp[current dice][current sum], but instead of calculating each state in O(k), you can maintain a partial sum table on the previous line(you can maintain it even in the dp table itself), so dp[i][j] = sum[i - 1][j - 1] - sum[i - 1][j - K - 1], where sum[i][j] = sum[i][j - 1] + dp[i][j], so you can calculate each state in O(1). To use less memory you can notice that you only need the last line and you can keep only one variable which is the sum of the contiguous interval in the dp table from the previous line.
Thank you very much!!!
I coded it and it got AC, the code has been added to the entry.
Thank you again!
No problem! :)
Problem 3 can be solved by reduction to polynomial multiplication.
The idea is to calculate the coefficient near XS in the following polynomial: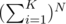 . If you'll use binary exponentiation with FFT multiplication and discard all coefficients near Xj where j > S on each iteration of exponentiation, your solution will work in
. If you'll use binary exponentiation with FFT multiplication and discard all coefficients near Xj where j > S on each iteration of exponentiation, your solution will work in 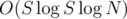 . It can be useful if your N will be pretty large.
. It can be useful if your N will be pretty large.
Hi, thanks for sharing your idea. Unfortunately, it is really hard for me to understand it completely because I don't know anything about FFT :(
But is it clear for you how to implement a solution without FFT in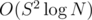 ?
?
Not that much. Can you try to explain it in more detail, please?
Maybe I didn't understand something, but in the second problem, why is it O(T * N * K2). The restriction of using at most k coins makes no sense if the goal is k dollars (using more than k coins of any type would result in more than k dollars). So the transition is DP[i][k] = DP[i - 1][k] + DP[i][k - Ci], where Ci is the current coin's value.
But we can use Ci more than once so DP[i][k]=DP[i-1][k]+DP[i-1][k-Ci]+DP[i-1][k-2*Ci]+... and that's why it is O(T*N*K^2).
I think you mean DP[i][k]=DP[i-1][k]+DP[i-1][k-Ci]+DP[i-1][k-2*Ci]+...
tenshi_kanade is pointing out that DP[i-1][k-Ci]+DP[i-1][k-2*Ci]+... = DP[i][k-Ci].
Thank you tenshi_kanade and ffao. I feel stupid now :D :D :D
I coded it and it got AC, but I think it's kinda strange, isn't it:
Recursion + memoization runs in 1.924s giving TLE.
Iterative DP runs in 0.552s and got AC.
You got lucky with that AC, it seems. Isn't
state[i][j-a[i]]undefined behavior when a[i] > j?Changed, thanks again!
For the first problem, it's clear that we need to add all reversed edges in the tree, so now we just need to partition these edges into the minimum number of paths. I'm claiming this can be done greedily (i.e. find any path that is as long as possible, and remove it). I'm not too sure how to do the formal proof of correctness, but one way to see why this is true is that when we "merge" two edges into one path, we reduce the number of paths by 1, and it doesn't matter what choices of "merge" we make.
Now using this observation, we can come up with an algorithm. Let in[i] be the number of incoming edges to i and out[i] be the number of outgoing edges. Then, the answer is sum(in[i] — out[i]) for all in[i] that exceed out[i]. The way we can see why this would be true is paths can only end at nodes where the indegree is bigger than the outdegree, so we just count this quantity directly.
Question about in[i] and out[i]:
Are we talking about the edges of the initial graph or about the reversed edges?
The reversed graph. Actually, I just realized that my solution is wrong, since I assumed paths are disjoint. I'm sure there is a simple modification so that they don't have to be disjoint, but I'll have to think about it a bit more.
Actually in both cases the algorithm fails for this test case:
6
0 2
1 2
2 3
3 4
3 5
The algorithm will return 3 but the answer is 2.
For the first problem first note that a tree with directed edges is a dag. Now the problem becomes in adding the minimum number of edges to a dag in order to make it connected.
It seems that the answer is the maximum between number of nodes that have zero out-degree and number of nodes that have zero in-degree. The main idea (let's say that the out-degree zero nodes are the maximum) of this is to join the nodes with out-degree zero to the nodes with in-degree zero (an edge for each one). I don't have a formal proof, though.
You can't add any edge to that DAG, though. Try this case: