shuprog1's blog

How to solve this problem?
By shuprog1, 10 years ago, In English

The problem statement is as follows: Problem description.

Little Schrodinger had a magical cat. That cat once fell down an empty well. As the walls of the well were not completely vertical, the cat could climb up the well. In one day, the cat can climb 1 unit height and the height of the well is h units. The cat starts at the bottom. Every day, a cat would divide into 2 cats. One of them would climb up 1 unit. The other would wait for help. But while waiting it would fall asleep and roll down 1 unit, unless it is already at the bottom, in which case it just remains there. When a cat would reach the top, it would run home to Schrodinger. (Schrodinger doesn't know that some of the cats are in a well and so he can't rescue them). It has been d days since the cat fell into the well. How many cats would come out of the well today? You would notice that the number of cats grows very large with each passing day, so output the answer modulo 10^9+7. NOTE : d = 0 means that the cat has fallen just now and so there's just one cat at the bottom of the well. So you wouldn't see any cat coming out today. If the height of the well is 1 unit, you will see a cat come out tomorrow.

Problem link : Cats of Schrodinger

  • Vote: I like it
  • -1
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 6   Vote: I like it +5 Vote: I do not like it

Let's define Ta as the (h + 1) x 1 matrix such that the (i + 1)th term (0 ≤ i ≤ h) contains the number of cat at position i in time a, then, Ta and Ta + 1 is related by (let's assume h = 4) :

Ta + 1 = A * Ta, where A =

and T0 =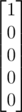

To calculate Td = Ad * T0, notice that Ad = Ad / 2 * Ad / 2 * (d mod 2 = 1?A: I),

thus we can use double powering to calculate Ad using O(h6*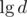) time. And the answer is the (h+1) term in Td

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you please explain how you came up with matrix A?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      with Square Matrix Exp, this same main idea of fast exponentiation of integers

      for example: A^40 = A^8 * A^32 = (A^1)^0 * (A^2)^0 * (A^4)^0 * (A^8)^1 * (A^16)^0 * (A^32)^1

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      well let's look at the first row, [1 1 0 0 0] what does it mean? It means that number of cats on position 0 is 1 * (previous number of cats on pos 0) + 1 * (previous number of cats on pos1). how about second row [1 0 1 0 0]? it means that number of cats on position 1 is 1 * (previous number of cats on pos 0) + 1 * (previous number of cats on pos 2). The other rows are similar.

      → Reply