522A - Reposts

Для решения этой задачи надо было проитерироваться по записям о репостах и поддерживать для каждого пользователя длину цепочки, которая заканчивается в нем. Здесь удобно воспользоваться ассоциативным массивом из строки (имени пользователя) в целое число (длину цепочки). Например, для С++ такой структурой данных будет просто map<string,int>. Назовем такую структуру chainLengths, тогда при обработки строки вида <<a reposted b>> надо просто выполнить присвоение chainLengths[a] = chainLengths[b] + 1. В качестве ответа надо вывести максимальное из значений chainLengths, что можно подсчитывать на лету.

Пара тонкостей: в начале надо занести chainLengths["polycarp"] = 1;, а всюду при работе со строками приводить их к нижнему регистру (или верхнему), чтобы сделать сравнение строк нечувствительным к регистру букв.

Пример такого решения: 10209456.

522B - Photo to Remember

В этой задаче для каждого i фактически надо было найти:

• W_i, равное сумме всех заданных w_j без w_i,
• и H_i, равное максимуму всех h_j без h_i.

Для подсчета первой величины достаточно найти сумму s всех значений w_j, тогда W_i = s - w_i.

Для подсчета второй величины достаточно заметить, что либо искомое значение есть просто максимум по h, либо (если h_i совпало с максимумом) это второй максимум (т.е. предпоследний элемент при сортировке по неубыванию). Второй максимум, как и максимум ищется за один проход по массиву.

В таком случае, для нахождения как W_i, так и H_i требуется O(1) действий, то есть O(n) суммарно на всё решение.

Пример решения: 10193758.

522C - Chicken or Fish?

Для решения задачи необходимо заметить, что при наличии недовольных пассажиров (т.е. тех, для кого r_i = 1), существенную роль играет только первый из них, так как остальные вполне могут быть недовольными именно тем блюдом, которое не хватило первому из таковых.

Пусть массив b — это массив максимальных возможных количеств порций каждого из блюда на момент старта обслуживания Поликарпа. То есть просто массив b надо заинициализировать массивом a, а каждый раз, когда t_i отлично от 0, то делать b[t_i] = b[t_i] - 1 (уменьшать количество порций блюда). Кроме того, пусть unknown — это количество пассажиров, про которых неизвестно какие точно блюда им достались (то есть для них t_i = 0). Пусть величина unknownBeforeUpset — это такое же количество, но до первого недовольного.

Таким образом, есть два основных случая:

• недовольных пассажиров нет вообще, тогда блюдо i могло закончится тогда и только тогда, когда b[i] ≤ unknown (жадно отдаем это блюдо всем пассажирам, для кого их точное блюдо неизвестно),
• недовольный пассажир есть, этот случай разберем подробнее.

Каким блюдом мог быть недоволен первый из таких пассажиров? Очевидно из списка кандидатов надо выкинуть все такие блюда, которые упоминаются не раньше него (значит, что они закончится до него не могли). Из оставшегося набора блюд достаточно перебрать все блюда и проверить могли ли они закончиться до этого пассажира. То есть блюдо i могло быть тем блюдом, что привело в недовольство первого недовольного, если одновременно верно:

• это блюдо i не упоминается на этом пассажире или позже,
• это блюдо i такое, что b[i] ≤ unknownBeforeUpset.

Для всех таких блюд, очевидно, в ответе должно стоять Y (они могли закончится к Поликарпу). Кроме того, из всех таких блюд наибольшую степень свободы дает блюдо с наименьшим расходом (количеством порций b[i]). Выберем именно такое блюдо и в остаток пассажиров с неизвестным блюдом restUnknown = unknown - b[minFirstFinished] попробуем поместить все вхождения каждого из других блюд. То есть блюдо j могло закончится до Поликарпа тогда и только тогда, если для него b[j] ≤ restUnknown (то есть закончилось то блюдо, что расстроило первого из недовольных, а следом — j-е).

Такое решение работает за O(m + k).

Пример решения: 10212686.

522D - Closest Equals

Воспользуемся тем, что задача задана в офлайн-формулировке, то есть все запросы можно считать до нахождения ответов на них.

Пройдем слева направо по массиву и составим новый массив b, записав в b[j] расстояние до ближайшего слева парного j-му элементу значения, то есть a[j - b[j]] = a[j]. Если такового нет, то запишем в ячейку бесконечность.

Эти значения соответствуют расстояниям между парными элементами и записаны они в позициях правых элементов в этих парах.

При рассмотрении запроса на отрезке [l, r] нам не нужны вообще такие пары, что начинаются левее l, а минимум надо искать среди пар, что заканчиваются не правее r.

Отсортируем все запросы по l слева направо. Тогда при прохождении по запросам можно поддерживать, что для запроса [l, r] в массиве b установлены бесконечности для всех пар, в которых левый элемент левее l. Для этого просто предподсчитаем для каждого элемента ближайший справа парный next[i] (то есть верно, что b[next[i]] = next[i] - i), и при покидании ячейки i будем записывать в b[next[i]] значение бесконечность.

В таком случае, для ответа на запрос [l, r] надо просто найти минимум на префиксе до индекса r включительно по массиву b. Это можно делать быстро разными способами (дерево отрезков, дерево Фенвика).

Асимптотическая временная сложность такого решения составляет .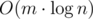

Пример решения: 10192075.