523A - Поворот, отражение и масштабирование

Это была несложная задача на технику работы с двумерными массивами. Для решения задачи можно было честно последовательно проделать все три операции или заметить, что первые две (поворот + отражение) совместно дают простую транспозицию (отражение относительно главной диагонали, когда клетка с координатами (i, j) отображается на клетку с координатами (j, i)). Поэтому для вывода ответа было достаточно сделать два цикла (используется 0-индексация и псевдоязык):

for i = [0...2*a-1] begin
  for j = [0...2*b-1] begin
    print(a[i / 2][j / 2])
  end
  вывести перевод строки
end

Пример решения: 10286345.

523B - Усреднение обращений

Подсчет приближенного среднего подробно описан в условии задачи (даже приведен псевдокод). В самом деле при его подсчете надо было просто следовать описанным правилам подсчета.

Для подсчета среднего на отрезках длины T достаточно знать значение суммы элементов на отрезках длины T (для получения среднего надо просто значение суммы делить на T). Если это делать наивным способом, подсчитывая сумму каждый раз в цикле заново, то получается неэффективный медленный алгоритм. В самом деле, при T = n / 2 и наборе из m = n запросов n / 2 + 1, n / 2 + 2, ..., n такой алгоритм суммарно выполнит около n² / 4 действий. Для заданного максимального значения n эта величина будет слишком большой для вычисления в 4 секунды.

Для ускорения подсчета суммы на отрезках длины T можно либо поддерживать эту сумму, тогда при перемещении старта такого отрезка с индекса i на индекс i + 1 сумма изменяется следующим образом: sum:  = sum - a[i] + a[i + T]. Таким образом, пересчет суммы от предыдущего положения старта отрезка до нового будет работать за одну формулу (ограниченное сверху некоторой константой количество действий).

Второй вариант как быстро находить суммы на отрезках состоит в подсчете вспомогательного массива частичных сумм. Пусть b[i] — сумма первых i элементов массива a. Тогда сумма элементов массива a на отрезке от l до r равна b[r + 1] - b[l] (если массив a 0-индексирован). Подсчет массива b можно осуществить за один проход слева направо по формуле b[i] = b[i - 1] + a[i - 1].

Пример решения: 10291184.

523C - В поисках имени

Наивный способ решения задачи (перебрать разрез и проверить "хорошесть" каждого из них) работает за квадратичное время и недостаточно эффективен, чтобы решение прошло.

Посчитаем две позиции:

• такую минимальную позицию l, что подстрока t[1..l] хорошая, тогда очевидно, что любой разрез за позицией l будет таким, что левая часть "хорошая",
• такую максимальную позицию r, что подстрока t[r..|t|] хорошая, тогда очевидно, что любой разрез перед позицией r будет таким, что правая часть "хорошая".

Каждую из величин l и r можно найти жадным образом просто итерируясь до вхождения очередной буквы и продолжая поиск следующей. Вот пример возможного кода для поиска l:

j := 1
for i := 1 to |t|
    if j <= |s| && s[j] == t[i]
        j = j + 1
        if j = |s| + 1
            l := i

Для того, чтобы после разреза обе части содержали s необходимо и достаточно, чтобы разрез проходил между l и r. Таким образом, ответ равен r - l или 0, если l или r не нашлось или r < l.

523D - Статистика обработки роликов

Для эффективной реализации алгоритма моделирования процесса необходимо хранить в какой-то структуре h отсортированные моменты освобождения каждого из серверов. Сначала h состоит k единиц.

Будем обрабатывать ролики последовательно в хронологическом порядке. Для того, чтобы начать обрабатывать очередной i-й надо дождаться освобождения какого-либо сервера. Пусть ролик приходит в момент s_i и имеет длительность t_i.

Очевидно, что можно ждать освобождения до первого из моментов из h (так как первый — минимальный). Возможно, что дожидаться в явном виде и не надо, так как сервер уже освобождается к моменту s_i, в любом случае можно считать, что ролик надо отправить на первый из серверов, который освободиться. Пусть минимальный элемент из h равен h₀, тогда ролик начнется обрабатываться в момент max(h₀, s_i), а закончит к моменту max(h₀, s_i) + t_i. Для поддержания структуры h надо исключить из нее h₀ и добавить max(h₀, s_i) + t_i. Таким образом, в h по прежнему будут все моменты освобождения серверов.

Для того, чтобы решения быстро работали, h надо хранить в подходящей структуре данных. Это может быть очередь с приоритетами (тогда минимум будет в голове), либо в упорядоченном множестве. Так как в h могут быть равные элементы, то эта структура либо должна работать с одинаковыми элементами (как очередь с приоритетами или мультимножество по типу std::multiset в C++) или надо в структуре хранить пары (момент освобождения, номер сервера).

Кроме того в качестве h можно использовать классическую бинарную кучу или упорядоченный ассоциативный массив (TreeMap в Java).

Такое решение будет работать за .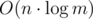

Пример решения: 10290987. В этом решении в очереди с приоритетами q моменты хранятся со знаком минус, чтобы сортировка по-умолчанию ставящая максимум вперед, ставила вперед минимум.