#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	164
1	maomao90	164
3	Um_nik	163
4	atcoder_official	160
4	adamant	160
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
8	Dominater069	154
8	nor	154

Problemsets slightly differ in main round and in an online mirror, in editorial problems follow in an order of the main round.

524A - Возможно, вы знаете этих людей?

This problem didn't appear in an online mirror. Its editorial will be left as an exercise in Russian language for those who are curious what it is about =)

524B - Фото на память - 2 (round version)

In an original version there was no constraint that no more than n / 2 friends should lie. This version can be solved pretty easy. Iterate over all possible values of H. For a fixed H we have to minimize total width of all rectangles on the photo. So, for each rectangle we need to choose in which orientation it fits into photo having the minimum possible width.

529B - Group Photo 2 (online mirror version)

In an online mirror version the problem was slightly harder. Let's call people with w ≤ h \textit{high}, and remaining people \textit{wide}. Let's fix photo height H. Let's consider several following cases:

If a high person fits into height H, we leave him as is.
If a high person doesn't fit into height H, the we have to ask him to lie down, increasing the counter of such people by 1.
If a wide person fits into height H, but doesn't fit lying on the ground, then we leave him staying.
If a wide person fits into height H in both ways, then we first ask him to stay and write into a separate array value of answer decrease if we ask him to lie on the ground: w - h.
If somebody doesn't fit in both ways, then such value of H is impossible.

Now we have several people that have to lie on the ground (from second case) and if there are too many of them (more than n / 2) then such value of H is impossible.

After we put down people from second case there can still be some vacant ground positions, we distribute them to the people from fourth case with highest values of w - h. Then we calculate the total area of the photo and relax the answer.

524C - The Art of Dealing with ATM

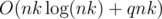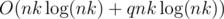Intended solution has the complexity $\text{[math]}$ or $\text{[math]}$ . For each possible value x that we can get write a pair (x, m) where m is number of bills to achieve this value. Sort this array in ascending order of x and leave only the best possible number of bills for each value of x. Then to answer a query we should iterate over the first summand in resulting sum and look for the remainder using binary search. The alternate way is the method of two pointers for looking in an array for a pair of numbers with a given sum that works in amortized O(1) time. Check that we used no more than k bills totally and relax the answer if needed.

524D - Social Network

Let's follow greedily in following way. Iterate over all requests in a chronological order. Let's try to associate each query to the new person. Of course we can't always do that: when there are already M active users on a site, we should associate this request with some existing person. Now we need to choose, who it will be.

Let's show that the best way is to associate a request with the most recently active person. Indeed, such "critical" state can be represented as a vector consisting of M numbers that are times since the last request for each of the active people in descending order. If we are currently in the state (a₁, a₂, ..., a_M), then we can move to the one of the M new states (a₁, a₂, ..., a_M - 1, 0), (a₁, a₂, ..., a_M - 2, a_M, 0), ... , (a₂, a₃, ..., a_M, 0) depending on who we will associate the new request with. We can see that the first vector is component-wise larger then other ones, so it is better than other states (since the largest number in some component of vector means that this person will probably disappear earlier giving us more freedom in further operations).

So, all we have to do is to simulate the process keeping all active people in some data structure with times of their last activity. As a such structure one can use anything implementing the priority queue interface (priority_queue, set, segment tree or anything else). Complexity of such solution is $\text{[math]}$ .

524E - Rooks and Rectangles

Let's understand what does it mean that some cell isn't attacked by any rook. It means that there exists row and column of the rectangle without rooks on them. It's hard to check this condition, so it is a good idea to check the opposite for it. We just shown that the rectangle is good if on of the two conditions holds: there should be a rook in each row of it or there should be a rook in each column.

We can check those conditions separately. How can we check that for a set of rectangles there is a point in each row? This can be done by sweeping vertical line from left to right. Suppose we are standing in the right side of a rectangle located in rows from a to b with the left side in a column y. Then if you denote as last[i] the position of the last rook appeared in a row number i, the criteria for a rectangle looks like 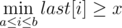$\text{[math]}$ . That means that we can keep the values last[i] in a segment tree and answer for all rectangles in logarithmic-time. Similarly for columns. This solution answers all queries in off-line in time O((q + k)log(n + m)).

524F - And Yet Another Bracket Sequence

The main idea is that the bracket sequence can be seen as a sequence of prefix balances, i. e sequence (a_i) such that a_i + 1 = a_i ± 1.

Calculate the number of opening brackets A and closing brackets B in original string. It is true that if A > = B then the string can be fixed by adding A - B closing brackets at the end and shifting the resulting string to the point of balance minimum, and if A ≤ B, then the string can be similarly fixed by adding B - A opening brackets to the beginning and then properly shifting the whole string. It's obvious that it is impossible to fix the string by using the less number of brackets. So we know the value of the answer, now we need to figure out how it looks like.

Suppose that we first circularly shift and only then add brackets. Suppose that we add x closing brackets. Consider the following two facts:

If it is possible to fix a string by adding closing bracket to some x positions then it is possible to fix it by adding x closing brackets to the end of the string.
From all strings obtained from a give one by adding closing brackets to x positions, the minimum is one that obtained by putting x closing brackets to the end.

Each of those statements is easy to prove. They give us the fact that in the optimal answer we put closing brackets at the end of the string (after rotating the initial string). So we have to consider the set of the original string circular shifts such that they transform to the correct bracket sequence by adding x = A - B closing brackets to the end and choose the lexicographically least among them. Comparing circular shifts of the string is the problem that can be solved by a suffix array. The other way is to find lexicographical minimum among them by using hashing and binary search to compare two circular shifts.

The case when A ≤ B is similar except that opening brackets should be put into the beginning of the string.

So, overall complexity is $\text{[math]}$ .

Comments (15)

Write comment?

Temirulan

10 years ago, # |

Thanks for editorial, F is good)

→ Reply

kingofnumbers

it's not necessary to use data structures in problem D , it can be solved in O(n) here is my submission 10386806

waterfalls

During the contest, I had all of that for F (A in mirror) except

"shifting the resulting string to the point of balance minimum"

I couldn't prove that it was always possible to make the string work using the lower bound of |A - B| brackets (indeed I thought this wasn't true, didn't even submit as a guess). How can you prove this?

ed1d1a8d

10 years ago, # ^ |

Lets say the length of the string is N for convenience. In the string, let '(' be +1 and ')' be -1. For a balanced string (equal number of '(' and ')' ), the total sum of the string will be 0.

In order to make any balanced string a valid sequence, first write out the prefix sums of the string (with +1 and -1). If the indexes are 0-indexed, then the prefix sum at i: PS_i = S₀ + S₁ + ... + S_i. We want to shift the string such that PS₀, ..., PS_N - 1 ≥ 0

Next, find the index at which PS is minimum (any index will do if there is a tie), call this index x ( PS_x = min(PS₀, ..., PS_N - 1) ). Let's call S[0...x] A, and S[x + 1...N - 1] B.

Now, if PS_x ≥ 0, the sequence is already valid.

If not, then we shift B to the beginning of the string. So if before S = A + B, now S' = B + A. Note that the sum of B is - PS_x, so in S' = B + A the minimum prefix sum in A will be - PS_x + PS_x = 0. Additionally, we know the minimum in B can't be less than 0, or else there would have been an element less than PS_x in S = A + B. Hence, S' = B + A will "fix" the string, as all prefix sums will now be greater than or equal to zero.

magemerlin

← Rev. 12 →

There exists O(n) solution of F.

Sequence of brackets can be considered as function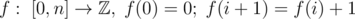 $\text{[math]}$ , if S[i] is opening, and - 1 in other case. Sequence of brackets is correct if and only if f ≥ 0 and f(n) = 0. As in $\text{[math]}$ solution, note that

additional brackets can be defined from f(n)
additional brackets in optimal solution go continuously (as single segment)

Lets precompute f, minleft[i] = min {f(j)|j < i}, minright[i] = min {f(j)|j > i}, increasing[i] = (length of maximum increasing sequence with beginning at f(i)).

New observation: let's consider f(n) < 0 and add - f(n) opening brackets before position i. In this case f(j), j < i will remain still, and f(j), j > i will increase by - f(n). Having minleft and minright, it is easy (O(1)) to check whether we will get correct sequence (shifting string if necessary).

Using previous observation and precomputed array increasing, we determine all positions where we can get correct sequence and choose only ones with maximum increasing[i].

After that, we use idea of two pointers (first and second) to find ultimate best position. First and second point to beginning of comparing subsequences. Obviously, these pointers must be ones of previous computation. This method gives linear time because we can keep comparing sequences not intersected: if on some step sequences are going to become intersected, we move one of pointers in the position after it's sequence and start comparison anew.

For example first = 0, second = 3

abcabcd

S[first + i] = S[second + i] for i = {0, 1, 2}

we move second to 6 and start comparison anew, comparing

S[first + i] with S[second + i] (first = 0, second = 6, i = 0, 1, ...)

instead of

S[first + i] with S[second + i] (first = 0, second = 3, i = 3, 4, ...)

because we already found out that S[0, 1, 2] = S[3, 4, 5].

I added some comments in hope that my code will help to figure out solution. http://codeforces.net/contest/524/submission/10398060

Swistakk

Where that $\text{[math]}$ comes from in F? It's clearly O(n). In CF when $\text{[math]}$ is expected then constraints are at most 3·10⁵ or sth, so I was afraid that $\text{[math]}$ can be too slow and coded O(n) solution. Suffix array can be constructed in O(n) and it is well known that we can get minimum values on all intervals of length k for a fixed array (which is necessary to check which shifts are allowed). Check my solution here: 10386965

riadwaw

← Rev. 2 →

Well, as far as I can tell usually it's not expected from participants to build suffix array in O(n) (Actually it's just dew times faster than NlogN version).

As for constraints, note 5s TL.

BTW, our NlogN solution takes just 0.5s, while your O(N) works in 1.8 :)

10382149

starius

Problem 524D (Social Network) can be solved in O(N), not in O(N ln N), if a circular buffer is used to keep non-expired users.

All operations happen with ends of user queue. New users are pushed to one end, last user's time is changed for a user from same end. Expired users are removed from another end. Pushing and updating time is O(1) per one operation, removing expired users is O(N) for all of them, because eventually we remove less then N users.

Check my solution here: 10480700

neelshahr92

Can someone explain the solution of the problem E — Rooks and Rectangles in detail? Help is appreciated.

jinzhihan

8 years ago, # |

I love you.

8 years ago, # ^ |

I love you, too.

I also love you.

ekzhang

Problem F can be solved in O(N) time using the skew algorithm.

sigma_g

4 years ago, # |

My brute force solution making roughly 5e8 operations in total passed for problem C The Art of Dealing with ATM. The solution is as follows:

Let us solve first query with value $$$x_1$$$. Pick a denomination and choose the number of times (<=k) you'll use it. This will be $$$5000\times k$$$ combinations. For each choice, you'll be left with some remainder $$$r = x_1 - c * d_i$$$, where you had chose the $$$d_i$$$ denomination $$$c$$$ times.

If $$$r=0$$$ we are done. Else, since the ATM only allows two different denominations, there must exist some $$$c_2 \le k - c$$$ such that $$$r$$$ is divisible by $$$c_2$$$ and $$$d_j = r / c_2$$$ is another denomination that exists in the set of all denominations. You can loop for all such $$$c_2$$$ and check for existence of $$$d_j$$$ in $$$\log n$$$.

In the end, complexity for one query is $$$5000\times k \times k \times \log 5000$$$. We have twenty such queries. So, expected complexity is around $$$4.91e8$$$ operations. It is still surprising to me that this passed by a really decent margin (293ms out of 2000ms allotted).

Submission link

Lates_

3 years ago, # |

Could you tell me how to find lexicographical minimum by using hashing and binary search in problem F? Thank you very much.