Привет.
Много раз слышал, что в этой задаче на высокий балл заходило решение с тернарником. Расскажите, пожалуйста, что за решение.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
12:11:05
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
12:11:05
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 05:23:56 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Если я ничего не упускаю, то
Запускаем тернарный поиск по x (ищем минимум)
Запускаем тернарный поиск по y (ищем минимум при фиксированном x)
Значение функции при фиксированном (x,y) — максимум расстояния от прямой до (x, y)
я пытался так делать, но даже 30 не набрал. мб я настолько хорошо написал. хотя есть вероятность, что тестирование на информатикс жестче, чем было на олимпиаде, потому что градиентный спуск, который якобы заходил на 90, заходит в дорешку только на 50.
спасибо за ответ ).
А у тебя границы в тернарниках правильно выставлены? Если что, ответ может лежать далеко за пределами ограничений на величину входных данных.
границы правильные. когда составлял уравнение прямых делил коэффициенты на сумму квадратов вместо ее корня -> 98 баллов.
Можешь показать свое решение?
У меня вот это проходит все маленькие тесты и заходит на 70 баллов, а на больших тестах банально не укладывается по времени.
Кажется, я уже разучился писать сколько-нибудь оптимальный код.
можно набрать 84, взяв вместо 100 71 )
98 баллов набирается за счет строк 122-127.
Если я правильно помню, одна из необходимых оптимизаций для этой задачи – использование золотого сечения в тернарном поиске. Это дает ускорение в несколько (раз в 5, не меньше) раз, и решение спокойно проходит по времени.
И еще нужно отнормировать прямую, чтобы избавиться как от извлечения корня, так и от деления на него в самом вложенном месте.
Да, я додумался до того, чтобы сохранить нормы векторов нормалей в отдельный массив, но не додумался до того, что можно просто поделить коэффициенты.
Мне хотелось сказать еще в предыдущем комменте: "Только не говорите, что тут нужно использовать метод золотого сечения!" :)
Про золотое сечение довольно внезапно. Часто оно оказывается лучше обычного разделения на три равные части?
Нужно посчитать в 2 раза меньше значений функции, чем в тернарном поиске. Плюс сходится чуть быстрее: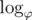
вместо 
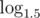. В случае вложенных поисков (как здесь) выигрыш, очевидно, значительный. Такое решение без проблем заходило на 100.
Если под градиентным спуском ты подразумеваешь популярную штуку типа "возьмем K точек из окрестности, пойдем в лучшую, уменьшим шаг" (что не совсем градиентный спуск), то насколько я помню, я смог запихать это максимум на 70+ баллов.
А вот честный градиентный спуск, если я ничего ни с чем не путаю, сойдется к оптимальному ответу в худшем случае за две итерации, итого получаем несложное линейное решение (правда, с разбором случаев).
Само по себе рассуждение такое (для случая, когда у нас есть три попарно пересекающихся прямых, являющихся наиболее удаленными для оптимального ответа). Берем некую произвольную точку и находим прямую, наиболее удаленную от нее. Двигаемся по перпендикуляру к ней (то есть, по градиенту функции f(x, y)) до тех пор, пока ответ уменьшается. Теперь у нас уже две прямых, являющихся наиболее удаленными от нашей точки. Далее мы вновь двигаемся по градиенту, то есть в направлении пересечения этих двух прямых, также до тех пор, пока ответ уменьшается. Теперь у нас есть уже три прямых, наиболее удаленных от нашей точки. Очевидно, что дальше мы сдвинуться уже никуда не можем, поэтому выводим ответ.
Для вырожденных случаев рассуждения аналогичные, но желающие, я думаю, разберут эти случаи самостоятельно.