I was trying to solve Timus 1032. Find a Multiple after several unsuccessful tries I made for fun submission with code and got AC now I am wondering why and how? My solution idea: if solution exists then we can arrange solution numbers to be prefix of rearranged sequence, since we don't know how to get those numbers just pick them randomly by shuffling sequence array if by change we get that those numbers form prefix we have solution. Repeat shuffling until we have solution or report that there is no solution if we are getting close to TLE.
I think that my solution should be incorrect because if we would have sequence with length n and there would be single unique solution of length k then the probability to guess right would be k! * (n - k)! / n!.
So I would like to ask if my solution is correct, if so why?
P.S. I know O(n), solution.











It is correct that the probability would be "k! * (n - k)! / n!" if the answer is unique, but it turns out that such testcase can't exist. That took me quite a while to figure out but here is my theory:
Let's have the numbers shuffled in some random order in array A. Now denote:
If for some i, we get S[i]=0, then that's a solution. However, suppose we don't get value 0. Then we are left with N values — S[1], S[2], S[3] ... S[N], and each of them can take a number between 1 and N-1. Pigeonhole principle obviously shows that two of the values must be equal. So let's suppose that S[i]=S[j] and i<j. Then:
So we prove that regardless of how the array is shuffled, there is always at least one continuous subarray of adjacent elements that is a solution to our problem. Well then, what are the odds that our solution subarray turns out to start at the first element? Well it's got to start somewhere, so that's right — 1/N. So each time you shuffle and try to find a prefix-solution, you've got about 1/N chance to get it right (in practice, probably higher). Your code performs 40,000 operations, which is in the worst-case 4N, so from probabilistic view it has a high chance to perform correctly :)
Nice analysis. Thanks for help!
So basically if we try to shuffle d times then probability of getting correct result is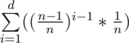 . And in my case if n = 104 and d = 4 * 104 it would be ≈ 0.98. So because of that my solution is correct?
. And in my case if n = 104 and d = 4 * 104 it would be ≈ 0.98. So because of that my solution is correct?
that's right. It is about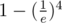 .
.
Btw. sample pesimistic case is N - 1 ones and one number equal to N. Then the only sequence giving you an answer is the one with number N in the beginning and prob. of it is exactly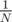 .
.
What is your O(n) solution btw.? I don't see any.
I is not mine, when I got AC I read it in comments. Suppose that
a[1], .., a[n]is original sequence. Then we can defineb[i] = (a[1] + a[2] + .. + a[i]) % nandb[0] = 0. Now from Pigeonhole principle we know that there must exist some pair b[i] and b[j] so thatb[i] = b[j], i > j, meaning that bothb[i]andb[j]produce the same remainder and their difference is divisible by n. So if we could find suchb[i]andb[j]the answer would bea[j + 1], a[j + 1], a[j + 2], ..., a[i - 2], a[i - 1], a[i]. So to get O(n) we just need to save the index of remainder when we calculate b array in some array m.Example: if sequence is
1 2 3 4 1We start by calculating:b[1] = 1, m[1] = 1
b[2] = 3, m[3] = 2
b[3] = 1, m[1] is already set, print answer: a[m[1] + 1], ... , a[3].
Linear solution follows directly from the reason his solution works, doesn't it? Just form array S and find the duplicating values :)
oh, thanks. It's obvious. Asking that question wasn't smart.