dalex's blog

Разбор задач Codeforces Round #301 (Div. 2)
By dalex, 10 years ago, translation, In English

540A - Combination Lock

For every symbol we should determine how to rotate the disk. This can be done either by formula: min(abs(a[i] - b[i]), 10 - abs(a[i] - b[i])) or even by the two for cycles: in both directions.

540B - School Marks

First count the number of marks that are less than y. If there are more than 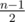such marks, we can't satisfy the second condition (about the median), and the answer is -1. Otherwise we can get exactly such number of y marks so that the total number of marks greater than or equal to y is at least 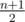(maybe it's already satisfied). This is the required action for satisfying the second condition.

Now, in order not to break the first condition, get the remaining marks as lower as possible — all ones — and check the sum of the marks. If it is greater than x, the answer is -1, otherwise the correct answer is found.

540C - Ice Cave

There are three cases here, though some of them can be merged.

  1. If the start and finish cells are equal, let's count the intact neighbours of this cell. If there is one, move there and instantly move back — the answer is YES. Otherwise it's NO.
  2. If the start and finish cells are neighbours, the solution depends on the type of the destination cell. If it's cracked, the answer is YES — we can just move there and fall down. Otherwise it must have at least one intact neighbour to get the positive answer — we can move to the finish cell, then to this intact neighbour, and then return to the finish cell.
  3. In the general case, check if the path from the start cell to the finish cell exists. If it doesn't, the answer is NO. Otherwise check the type of the destination cell. If it's cracked, it must have at least one intact neighbour, and if it's intact, it must have two intact neighbours.

540D - Bad Luck Island (my code: http://pastebin.com/3s6dRK3A)

Let's count the values dp[r][s][p] — the probability of the situation when r rocks, s scissors and p papers are alive. The initial probability is 1, and in order to calculate the others we should perform the transitions.

Imagine we have r rocks, s scissors and p papers. Let's find the probability of the rock killing scissors (the other probabilities are calculated in the same way). The total number of the possible pairs where one species kills the other one is rs + rp + sp, and the number of possible pairs (rock, scissors) is rs. As all meetings are equiprobable, the probability we want to find is 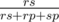. This is the probability with which we go the the state dp[r][s — 1][p], with the number of scissors less by one.

In the end, for example, to get the probability of the event that the rocks are alive, we should sum all values dp[i][0][0] for i from 1 to r (the same goes to the other species).

540E - Infinite Inversions (my code: http://pastebin.com/QFEMRbNP)

At first find the position of each element which is used in swap (using map). Now let's find the answer. It consists of the two parts. First part is the number of inversions formed by only whose elements which took part in the swaps. They can be counted by one of the standard ways: mergesort or Fenwick tree. The second part is the number of inversions formed by pairs of elements where one element has been swapped even once, and the other element stayed at his position. Let's consider the following test:

2
2 6
4 8

The global sequence will look as follows: [1 6 3 8 5 2 7 4 9 ...], and here is the array of swapped elements: [6 8 2 4].

Let's understand with which numbers the number 8 forms the inversions. The only elements that could do that are the elements between the initial position of the number 8 (where the number 4 is now) and its current position: [5 2 7]. There are two numbers on this segment which didn't take part in swaps: 5 and 7. The number 2 should not be counted as it took part in the swaps and we have already counted it in the first part of the solution.

So we should take the count of numbers between 8's indices in the global sequence (8 - 4 - 1 = 3) and subtract the count of numbers between its indices in the swaps array (4 - 2 - 1 = 1). We'll get the number of inversions formed by the element 8 and the elements which haven't moved at all, it's 2. Counting this value for all elements which have been swapped at least once, we get the second part of the answer. All operations in the second part of the solution can be performed using sorts and binary searches.

  • Vote: I like it
  • +103
  • Vote: I do not like it

Comments Comments (62)
| Write comment?
»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Well, I think, it would be great if the meanings of 'global sequence' and 'swaps array' is made clear in E's explanation (in paragraph 4 if the test case isn't counted). Do they mean 'the permutation' and 'the swapped elements' in the second paragraph...?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +10 Vote: I do not like it

    Yeah, "global sequence" == "permutation" and "swaps array" == "the swapped elements" (fixed)

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Thanks for fixing, and thanks for the short & clear explanation!

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Thanks for the editorial! If I may ask quickly about question B, I'm still a bit confused as to how the (n-1)/2 check works for the median. For example if given original grades 3, 5, 6 and minimum median of 6, with value k=50 and x=999, wouldn't it be easy to add 50 values to {3, 5, 6} such that the median exceeds 6 and sum<999? Yet with the editorial it says if at least (n-1)/2 marks are less than the median ie: (3-1)/2 = 1, marks are <= median (which there are since 3, 5, and 6 are <=6}, how does it mean we can return -1?

Thanks, sorry if this is a dumb question, I'm just really confused.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Seems like you mistook n and k.

    In the example where Vova needs 49 (the problem says it's an odd number) tests and finished 3, n = 49, and k = 3. Therefore, (n — 1) / 2 is 24 instead of 1. Then, of course, the answer is -1 if there are 24 marks that are less than y, instead of 1 :)

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Oh... I see now, the variable "n" was referring to ALL the course marks and not just the ones that were currently given... I didn't read the question very well; but hoping to do better next time, thanks for the problems!

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The number 3 in your formula (3-1)/2 is k, but it must be n, I think that's where you are wrong.

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Edit: No need to read this. I have caught my mistake. A reading error :) One more Question for Problem B. If suppose the input is n=5 and k=3 and the minimum median is 4 and the given input is 444. So this fails the (n-1)/2 condition, but still 44444 for example is a solution (assuming sum is large enough). Sorry if it is dumb question(hopefully it is not) :) Did not read the solution carefully. My mistake. No need to reply to this.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This mistake was fixed about 30 minutes ago, maybe you haven't updated the page since that time? Now that statement says about elements less than y.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yes, I just refreshed and saw that. Then I updated my post, thinking I read wrong. But thanks, I did not read wrong and now it has been corrected. :)

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In problem D, if all the meetings are equiprobable the probability that we have minus one scissor would not be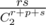 instead of 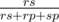. Why we don't count the meetings between the same kind?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    It's a conditional probability: the probability of the fact that rock kills scissors, given that somebody dies.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      But the question D says any two random individuals meet so why isn't 2 people from whole set included as said above by Empty.I mean why is that wrong if we consider the whole people left as our sample space for choosing two people.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        If two of the same types are chosen, we are back with the same state as before: nothing changes. We just go again, and we keep going until different types are chosen. Until that happens, nothing changes so the same state is preserved.

        As dalex said, we only calculate probabilities of the different events given that something changes.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          But, it will not affect the result of the probabilities?, it would be interesting to see a math proof to show how it works.

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            What's confusing is that we are conditioning this on the fact that a single type wins, and also we are not at all interested in the number of trials this takes. Meaning, we aren't checking the probability of the case that all three types remain (ie: they keep meeting each other).

            So now, given that after some number of trials, a single type remains, we can effectively ignore all the trials where the same type meets.

            Again, we could not do this if we were calculating things like:

            1) number of trials until a specific type wins 2) probability that a single type will win given the possibility of an eternal tie

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              10 years ago, # ^ |
                Vote: I like it +1 Vote: I do not like it

              I get the same meaning like Empty said.I can't get the correctly example answer in my way.I think in most cases, you should read the problem without ambiguity or less.

              → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it +5 Vote: I do not like it

            math proof can be following:

            first, lets say that

            Crsp — all possible permutations of r s and p pairs.

            Crr, Css, Cpp — all possible permutations between (r and r), (s and s), (p and p) pairs respectively.

            Crs, Csp, Crp — all possible permutations between (r and s), (s and p), (r and p)

            (note that Crs = r *s, Csp = s * p, Crp = r * p)

            it's evident that

            Crsp = Crr + Css + Cpp + Crs + Csp + Crp

            now lets say that

            Prsp — is a probability for [r, s, p]

            Pr1sp — is a probability [r — 1, s, p]

            Prs1p — is a probability [r, s — 1, p]

            Prsp1 — is a probability [r, s, p — 1]

            note that meetings between r and r, s and s, p and p doesn't remove anything, so:

            Prsp = (Prsp * (Crr + Css + Cpp) + Pr1sp * Crp + Prs1p * Crs + Prsp1 * Csp) / Crsp

            multiply the equation by Crsp and move Prsp * (Crr + Css + Cpp) to the left part:

            Prsp * (Crsp — Crr — Css — Cpp) = Pr1sp * Crp + Prs1p * Crs + Prsp1 * Csp

            but Crsp = Crr + Css + Cpp + Crs + Csp + Crp, so:

            Prsp * (Crs + Csp + Crp) = Pr1sp * Crp + Prs1p * Crs + Prsp1 * Csp

            or:

            Prsp = (Pr1sp * Crp + Prs1p * Crs + Prsp1 * Csp) / (Crs + Csp + Crp)

            finally we know that Crs = r *s, Csp = s * p, Crp = r * p, so:

            Prsp = (Pr1sp * (r * p) + Prs1p * (r * s) + Prsp1 * (s * p)) / (r * s + s * p + r * p)

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it

              Nice. We obtain a recursive relation for Prsp. I mean Prsp = A * Prsp + something, a seemingly infinite recursion.

              → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 3   Vote: I like it +3 Vote: I do not like it

        I didn't use the conditional probability at all. See my code:10949419. I'm considering all possible pairs of meeting (the sample space is n*(n-1) / 2). However, I still got the same result. When 2 people of the same species meet, no one will die. This will lead to an infinite geometrics series when you calculate the probability that someone dies.

        [Edit] So, both methods are fine. If you do it without the conditional probability, but get a different result, you're calculating the probability wrong.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          p[i — 1][j][k] += ppp / (1 — ppp2); can you please explain what i am doing by this ppp / (1 — ppp2); ?

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Let's say we're interested in P[a rock dies].

            Case 1: a rock dies in the first meeting. P(1) = i * k / space(i + j + k)

            Case 2: no one dies in the first meeting, then a rock dies in the second meeting. P(2) = P[no one dies] * P(1).

            Case 3: no one dies in the first 2 meetings, then a rock dies in the third meeting. P(3) = P[no one dies]^2 * P(1).

            ...

            P[no one dies] = (space(i) + space(j) + space(k)) / space(i + j + k) = ppp2.

            So, P[a rock dies] = P(1) + P(2) + ... = P(1) + ppp2 * P(1) + ppp2^2 * P(1) + ppp2^3 * P(1) + ... = P(1) / (1 — ppp2).

            → Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Hey, why can't we use this recurrence relation instead: Considering dp[i][j][k] to be a struct with member functions r,s,p

    dp[i][j][k].r= 1/3.0 *( dp[i][j][k-1].r + dp[i][j-1][k].r + dp[i-1][j][k].r);

    Why is this logically incorrect?

    EDIT: Got it. All are taken different. I was taking all the rocks as same.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why my solution for D print wrong answer? I don't see anything different compared to the author's code.

10958659

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can someone help me to correct my algorithms for Problem-B(School Marks)

My SoutionSolution

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I just want to give you an advice (because I'm not familiar with Java). Your code is a bit complicated, to make it simpler, put the answer(s) to the problem into an array (or a vector). It is much easier to read, and of course, to write the code.

    Here is my C++ solution (with comments) for reference: pastebin

    Good luck!:)

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Thanks for the fast tutorial :)

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can anyone please explain how to calculate the probability in problem D?

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In problems C this case 7 1 X . . . X . . 5 1 3 1 Will fall at the beginning, and will not come up So the answer should be NO, but why the answer is YES Can you explain it ?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    From the statement: "the ice on the starting cell is initially cracked".

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      yes thinks. but i think starting will down , I read wrong .

      → Reply
»
10 years ago, # |
← Rev. 11   Vote: I like it 0 Vote: I do not like it

Umm i may have grossly misunderstood problem C here. Probably the word 'side adjacent' or 'fall down'. Help me out here. I used the BFS in a grid technique to get my answer. However, my code gives me 'YES' for example testcase 2. According to my logic, that should right. Here is the case:

5 4 .X.. ...X X.X. .... .XX. 5 3 1 1

We can go to 1,1 from 5,3 as follows:

(5,3)->(4,3)->(4,2)->(3,2)->(2,2)->(2,1)->(1,1)

Here is my code: http://ideone.com/JS4OAU

What's the flaw?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    When you reach (1, 1) for the 1st time, the ice from 'intact' become 'cracked', so you can't fall down yet. You must step on (1, 1) another time to fall down, but there's no room to do this, so the answer is 'NO'.

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

ALright so i've applied the concept of a BFS in a grid but my code keeps failing at Test case 21:

2 2 .. .X 2 2 1 1

Any ideas as to why it fails?

submission: http://codeforces.net/contest/540/submission/10967359

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Ok, I've had a lot of submissions and i'm thinking this cannot be done by BF Ssince there is not way of determinig whether the adjacent edges have been stepped on or not. They may have been discovered but no way to determine that they have been stepped on i believe. Not unless i find the actual shortest path using BFS and backtrack. I'm completely lost. Could someone help me? Is this solvable with BFS?. Here's a C++ code:

    http://codeforces.net/contest/540/submission/10968998

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      The insight is that you just need to find if the destination is reachable or not. It doesn't matter which path you take. Then at the destination, if you need an extra step on that, you just look around the 4 neighbors to see if at least two of them are dots. So you can move to one dot and move back again (assuming that you might step on another dot, while getting to the destination). There is also an edge case where you start from one of the 4 neighbors. In this case, you only need one dot.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        And at least a neighbor dot have visited to ensure it reachable from start point

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          No need. We already check if the destination is reachable or not. If it's reachable, it already guarantees at least a neighbor dot has been visited or the starting point is a neighbor.

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            Can you please tell me what will be the answer for this case? 3 1 X . X 1 1 2 1

            I think answer will be YES. Path: (1,1)->(2,1)->(1,1)->(2,1)

            Accepted codes give NO.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              10 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              you cannot go back to (1,1) because it's already cracked and you'll fall down.

              → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can anyone tell me why am I getting WA on test 55 problem C? flag=0 if destination cell is intact, else it is 1. Solution

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone please explain problem E in detail? I m not able to understand anything

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Which part are you unable to understand. Do you understand the question clearly?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I tried to understand his code. CODE

      Can you please tell me what he is doing in the last for loop of the main function and what is the function bs doing.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 4   Vote: I like it +6 Vote: I do not like it

        let me explain you the general approach. suppose you have the input as: 2 1 1000000000(10^9) 100 200000000(2*10^8)

        you obviously cannot create an array of size 10^9. so you create an array with only the elements which were swaped. So the array : arr[] = {1 , 100 ,200000000,1000000000 } we then compress this array as arr[] = {1,2,3,4} (100 is replaced with 2,200000000 with 3,1000000000 with 4) now apply the swaps then we get arr[] = {4,3,2,1} now we need to do 2 things 1) Count the inversions in the compressed array 2) Count the inversions in the original sequence which contains all the elements. Add the results of 1 & 2 you get the answer. How to solve 1 ? We can use merge sort : http://www.geeksforgeeks.org/counting-inversions/ or using a fenwick tree : http://pavelsimo.blogspot.in/2012/09/counting-inversions-in-array-using-BIT.html. ans = 0 number of elements less that 4 and to its right = 3. ans = 3 number of elements less that 3 and to its right = 2. ans = 5 number of elements less that 2 and to its right = 1. ans = 6. so the answer for the first part is 6.

        Now, How to solve the 2nd part ? (this is the last loop in the editorial solution) Getting back to our original sequence after swaping. seq = 1000000000,2,3,4,...98,99,200000000,101,102.........999999998,999999999,100,1 now how many inversions for 10^9 ? it's original position — current position so 999999999 but we have already counted the inversion made by 200000000,100,1 in the first part where they were compressed, so subtract 3.

        now inversions for 2*10^8 is also calculated in the same way.

        Now add the results of the 2 parts. Please go thorough the editorial code. the above is an explanation of that code. It is easy to understand.

        also have a look at http://codeforces.net/blog/entry/17643#comment-225956 that is what the last loop is for

        → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Here's my code that uses fenwick trees (Binary Indexed Trees) and lower_bound to solve this question.

        → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can some one explain why we need to do the second part in question E. Why cant we simply count the no. Of inversions using merge sort or a fenwick tree?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I understood it after understanding the question and solution clearly.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Because you will miss cases where first number is a moved one and the other one did not move.

    look at first input:

    after swaps it looks like:

    2,4,3,1,5....

    if you just consider pairs in which both elements have moved from original you will get:

    2,4,1

    this will give you 2 pairs (2,1) and (4,1) but what about (4,3) ? you will only get this, by the second method that has been explained.

    You cannot construct the complete tree and expect to iterate through it in timelimit that is set.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

is it just me or anyone else?

I wanted to practice on this round but find the image in Problem C is a dead image... http://codeforces.net/predownloaded/5b/ff/5bff99f4731b22c9ea00f830072ddfe7040ed80d.png

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I am trying to understand the following solution 10945934 for 2 days already.
I don't get the key part of the solution:

for (int i = 0; i < m; i++)
{
    int x = a[i];
    int pos = mapchik[x];
    ans += abs(b[i] - x) - abs(pos - i);
}

Could, someone please explain in as much detail as possible, how does this part of the code work?

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem D , i cannot understand the meeting probability . According to tutorial it's r*s / (r*s + s*p + p*r) for rock species meets/kills scissors species when they meet . Now i'm giving my view , i want to know whether it's correct or not .

Suppose at any situation we have r rocks, s scissors and p papers .

Now , let's find the probability to choose 1 rock species and 1 scissors species . say it's P(x)=(r/(r+s+p))*(s/(r+s+p-1)) . That means P(x)=(r*s)/((r+s+p)*(r+s+p-1)) .

again for 1 scissors species and 1 paper species . say it's P(y)=(s*p)/((r+s+p)*(r+s+p-1)) .

again for 1 paper species and 1 rock species. say it's P(z)=(p*r)/((r+s+p)*(r+s+p-1)) .

Now the probability of rock kills scissors = P(x) / (P(x)+P(y)+P(z)) .

it's equal to (r*s) / (r*s + s*p + p*r) . exactly the same as tutorial . Plz let me know whether i'm correct or not .

→ Reply