The last round for advancing into round 2 starts today at 12:00 MSK
Good luck
Edit : Its over, congrats to all who made it.
Practice Link thanks StoneCold_ for the tip
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3885 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3580 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3506 |
| 7 | ecnerwala | 3505 |
| 8 | Radewoosh | 3457 |
| 9 | Kevin114514 | 3377 |
| 10 | gamegame | 3374 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 170 |
| 2 | Um_nik | 162 |
| 3 | atcoder_official | 161 |
| 4 | -is-this-fft- | 160 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | maomao90 | 155 |
| 8 | adamant | 154 |
| 9 | luogu_official | 153 |
| 10 | awoo | 152 |
The last round for advancing into round 2 starts today at 12:00 MSK
Good luck
Edit : Its over, congrats to all who made it.
Practice Link thanks StoneCold_ for the tip
| Название |
|---|



How to solve C-large?
Greedily add the smallest coin you need.
Proof?
Add the denominations in increasing order. If you already have interval [1,x] and none of the already existing denominations can help you increase it, then if you add a denomination greater than x + 1, you won't be able to make (x + 1), if you add a denomination smaller than x + 1 you will get a smaller interval.
I think you need to explain a bit more if you actually want to help anyone who doesn't already get it.
Its easy to prove with induction. First sort all coins and take one at a time. If we have a set of coins which can reach all values less than n, and the next coin v is at most n + 1, then we will now be able to reach n + v * c. If however v is larger than n + 1, then we will not be able to reach n + 1, so we need to add that coin to our collection. This is also the best case, we could have added a smaller coin but it will only reduce our max reach in the future so there is no reason to do it.
Another solution (too complicated, I guess, but seems interesting to me :) )
Imagine that we are to check that existing values cover
0 ... v:we could iterate through them in decreasing order and recalculate
vas max(v - c·vali, vali - 1) and check ifv = 0in the end.So, let's do the following dymanic programming:
dp[add][i]-- minimumvwe can achieve if the firstivalues were used and we addedaddnew values.One can do transitions in O(1) (the best value to add for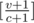 or
or 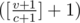 );
);  .
.
0 ... visI personally didn't take part and had no chance to submit my solution, but it seems not hard to prove the correctness of the following solution.
Suppose we have already managed to add coins in such a way that the requirements of the problem are fulfilled and we got all values in range [1,p] and considered first i-1 coins in sorted order. So now there is two cases to be considered.
1.a[i]<=p+1. This means that we can collect all the values until p+c*a[i] inclusive, so we can set i=i+1,p=p+c*a[i]. 2.a[i]>p+1. This means that we need to get all values in range [p+1,a[i]-1]. So it is better choice to add coins starting from value p+1. So here we need to decide how many coins to add starting from p+1 in order get values from required range. So we can make either binary search to find out exact number or write out sum of arithmetic progression and solve linear equation. Let k is that number, so we need to add all [p+1,p+k] coin denominations, like in the first case we will set i=i+1,p=p+sum[p+1;p+k]+(c-1)*sum[p+1;p+k] and we should increase answer by k.
I couldn't solve A large, any hints ?
For each row, except the last one you need to ensure that there's no way to place the ship.
The code is:
"""""""" answer = R*(C/W) + W;
if(C%W == 0)
--answer; """"""""""""
That means that you 'hit' all possible squares (C/W),and we multiply it by R. After the '+W' means that we fill correct final squares. the 'If' statement, decrease 'answer' by 1,because if W is multiple of C,then in our 'last' option we have one option instead of two.
What about B-large?
Dynamic programming: dp[ind][suff] — expected number bananas you will give monkey where covered ind letters and suffix with length suff is equal to prefix of target with length suff. Then iterate next letter and go to the state — (ind + 1, nsuff), where is nsuff the maximal length of suffix of current string equals to the prefix of target. Also be careful with state (ind, L). L = |target|.
But at the start you need to calculate how many bananas you need to bring. This value can be computed greedily (val).
Answer will be: dp[0][0] - val.
Code
You seriously over-complicated the problem, all you need to do is multiply all keystroke chances together, multiply this with the amount of characters typed by the monkey — target length +1 (the amount of places the string can appear at). This is the expected amount of bananas the monkey will get:
Won't this cause problems since getting a match on position i is not independent of getting a match on position i + 1 ?
Interdependence doesn't matter if we just seek the expected value. The problem setter might have missed this since it made the problem really easy, it is possible to solve this quickly even if the strings were of length 100,000.
The low limits for the Large were intentional and allowed solvers to use either DP or linearity of expectations.
"You seriously over-complicated the problem"
Well, I think I better not even mention my dp on Aho-Corasick solution =.=
You and me both. At least it worked.
Me too. I used a similar approach, but even more complex. I did DP[l][m][t], which means the probability that we reach a state with l letters typed, a current prefix match of length m and t full occurrences of target string. Then at each state, I checked the probability of typing all 26 letters and updated the next state. To check the next value of m at the transition, I used Z Algorithm / KMP's Failure Function.
The maximum bananas was the maximum value of t among all pairs {m, t} such that DP[S][m][t] > 0. And the expected bananas we keep is that minus t * DP[S][m][t] for all pairs {m, t}.
Won't the output be same for the following two test cases using this algo?
2 2 3 AB AA
and,
2 2 3 AB AB
No, the output of the program wont be the same since in the first case you need to bring 2 bananas while in the second case you only have to bring one banana. The expectation value of number of bananas the monkey will get is 0.5 in both cases though (which is whats calculated in my post), so the answer to the first is 1.5 and the answer to the second is 0.5.
Yes. I was talking about the expected number of bananas that the monkey will get only. Got confused, that, it is not the final answer. Thanks!
I have been wondering about how the expectation updating works. Your dp stores the expected values. Then you update a new expected value with an old expected value by doing something like
dp[i + 1] = p(i+1) * (1 + dp[i]). What is the principle behind this? I guess you use the law of total expectation:E(X) = sum(E(X|A_i) * P(A_i)). According to your code,P(A_i)should bep, andE(X|A_i)iscur + calc1(ind + 1, snuff). Am I right?First time I took first place in a competition! Yay me!
Cool. Any advice for how to practice and becoming better for beginners? I thought coming up for a solution for problem 2 and problem 3 was really tough. How to remove this mental block which comes up with every new problem?
I got an advanced degree in mathematics so my ability to reason about problems like these comes from many years of experience. It is kinda hard to distill that into a tip! But this is how I worked through the solutions:
Problem B is basic probability theory and some implementation.
Problem C is related to the number system; if you are only allowed to use one of each coin then the ideal solution is all powers of 2, with two of each it becomes all powers of 3 etc. Since you are forced to use some other coins as well this gets shifted a bit, but the general principle is the same.