Начал изучать потоки.
Пусть есть транспортная сеть G = (V, E). c(u, v) — пропускная способность. Если есть ребро (u, v), то нет (v, u). Исток s, сток t. Для любой вершины v верно то, что она достижима из s, и t достижима из v.
Пусть есть поток на этой сети f.
0 ≤ f(u, v) ≤ c(u, v).
Для любой 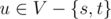 верно
верно 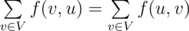 .
.
То есть всё как в Кормене (3 издание). У меня такой вопрос. Верно ли то, что исходя из ограничений на функцию потока мы не можем пропустить через какое-то ребро (u, v) вещества меньше чем f(u, v). Иными словами, верно ли то, что если мы доставили вещество в сток, то не существует ребра, через которое прошло вещества меньше, чем f(u, v)? Или я вообще спрашиваю глупость?=)











f(u, v) — это как раз поток через ребро (u, v)
Я хотел сказать следующее. Вот у нас рёбра выходящие из истока. Мы пускаем по ним количество вещества заданное потоком (то есть через них прошло вещества столько, сколько требует поток). Верно ли то, что и для остальных рёбер это произойдёт (то есть вещества по ним пройдёт f(u, v))? Походу я фигню всё таки спрашиваю=)
Мы по каждому ребру пускаем ровно f(u, v), да.
В этом и суть ограничения на суммы, что в вершинах ничего не остается.
А как доказать или где почитать, что по каждому ребру пройдёт ровно f(u, v)? Просто я могу доказать, что в вершинах ничего не останется, но не могу понять, почему все рёбра насытятся.
Не обязательно все ребра насытятся. Поток это функция f(u, v) (как sin(x)) от ребер, которая каждому ребру сопоставляет некоторое число, причем:
f(u, v) ≤ c(u, v)
f(u, v) = - f(v, u)
Для каждой вершины, кроме истока и стока, сумма потока по всем исходящим ребрам равна 0
Если немного поразмыслить, то такую функцию можно представить в виде потока некоторого вещества, где каждая единица потока, начиная свой путь из истока, идет в сток (по некоторому пути), причем по каждому ребру проходит не больше заданного для каждого ребра единиц потока.
Задача о максимальном потоке из всех потоков ищет такой, у которого величина (количество единиц потока нашедших свой путь из истока в сток) наибольшая.
Я попробую всё таки ляпнуть по-другому=) Вот мы нашли поток для графа. И мы ручками имитируем течение жидкости. То есть направим 1 литр в эту вершину и т.п.. Меня интересует, можно ли привести пример графа и потока, в котором мы через ребро направим жидкости меньше чем требует поток?
Если я правильно понял, то простой путь из трех вершин, у первого ребра пропускная способность 1, у второго — 2. По второму ребру никак не сможет пройти две единицы потока.
Если верно понял вопрос: представь граф из источника/стока и двух вершин посередине. Из источника идет по ребру в эти вершины и из каждой из этих двух вершин идет ребро в сток, у всех ребер пропускная способность = 1. Максимальный поток будет 2, а по каждому ребру пройдет 1.
Edit: кажется, все-таки не понял вопроса.
Ура я понял :)
То, о чем Вы говорите, называется декомпозиция потока.
Пока не понимаю то или не то. Но большое спасибо)
https://upload.wikimedia.org/wikipedia/commons/9/94/Max_flow.svg
Вот граф и поток. Обозначим за cnt(u, v) количество жидкости пройденное через ребро на момент, когда вся жидкость вышедшая из истока оказалась в стоке. Можно ли придумать граф и поток на нём, что cnt(u, v) < f(u, v) (исключаем рёбра исходящие из истока).
То есть например на рисунке я такое течение жидкости не вижу. Обязательно все рёбра придётся насытить и будет cnt(u, v) = f(u, v)
Читайте выше про декомпозицию)
Вообще это несколько философский вопрос, так как жидкость лишь помогает уловить суть математической модели. Скажем цикл (в который не входят ни исток, ни сток), в котором циркулирует единица потока, Вас устроит?) Т.е. в данном случае f(u, v) ребер цикла будут равны некоторой величине, но как таковой жидкости из истока в сток не притечет.
Да=) Пример с циклом работает=) Сейчас нарисую выложу=)
Отмечу, что теорема о декомпозиции говорит, что поток можно разбить на несколько путей из истока в сток и циклов, что через каждое ребро пройдет ровно f(u, v) путей и циклов. Т.е. это как раз то самое представление потока жидкости, если допустить циклы, и сказать, что жидкость по ним циркулирует просто так.
https://yadi.sk/i/xpTy2OWigpdCN
Пример, где верхние рёбра не насыщаются.
Всем спасибо!
Ссылка пишет, что ничего не найдено :(
Чтооо блин вообще?
Автора устраивал ответ "Да, в одной сети может быть несколько разных потоков"?