There is this classical problem of counting number of inversions in an array.
Let A[0...n - 1] be an array of n distinct positive integers. If i < j and A[i] > A[j] then the pair (i, j) is called an inversion of A.
This problem can be found here.
I found this problem on CF where we need to find number of such triples (i,j,k) such that i<j<k and A[i]>A[j]>A[k].
I solved both of the problems using BIT.
For the second problem, I counted number of numbers greater than A[i] at its left (left[i]) and number of numbers less than A[i] at its right (right[i]). So the output is summation of right[i]*left[i] for all i from 0 to n-1.
Now I have a question, what if the problem is counting inversions of length N? It means we need to find number of such combinations (i,j,k,...) such that i<j<k<... and A[i]>A[j]>A[k]>...
What should be a generalized solution for this problem?











You're just finding the number of decreasing/increasing sub-sequences of length N which is a known problem on spoj
it can be solved using dp, let dp[i][j] means the number of increasing sub-sequences of length j that ends in i so we have to formula to compute the dp:
dp[i][j] = sum for each index k such that k < i and A[k] < A[i] (dp[k][j - 1])
this is O(N2 * K). however, using BIT/segment tree can be done in O(N * KlogN)
Okay! It was just a simple observation.
Would you please enlighten on an implementation using segment tree?
Thanks!
here's my implementation to the problem on spoj link, it uses BIT but you can just implement the functions read and update using segment tree instead of BIT and it will be as you want
There are also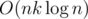 solution using mergesort.
solution using mergesort.
Problem in OJ: Timus
Solutions:
Mergesort
BIT
Policy based data structures
Can you explain your BIT solution? It would be helpful.