starius's blog

Maximum sum of all subarrays of size k for each k=1..n
By starius, 9 years ago, In English

Given an array of size n, for each k from 1 to n, find the maximum sum of contiguous subarray of size k.

This problem has an obvious solution with time complexity O(N2) and O(1) space. Lua code:

array = {7, 1, 3, 1, 4, 5, 1, 3, 6}
n = #array

function maxArray(k)
    ksum = 0
    for i = 1, k do
        ksum = ksum + array[i]
    end
    max_ksum = ksum
    for i = k + 1, n do
        add_index = i
        sub_index = i - k
        ksum = ksum + array[add_index] - array[sub_index]
        max_ksum = math.max(ksum, max_ksum)
    end
    return max_ksum
end

for k = 1, n do
    print(k, maxArray(k))
end

Is there any algorithm with lower time complexity? For example, O(N log N) + additional memory.

I asked this question on stackoverflow.

Related topics:

  • Vote: I like it
  • +14
  • Vote: I do not like it

Comments Comments (6)
| Write comment?
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I don't know better than O(n2) solution, but the second problem has solution with monotonic queue.I'll think for better solution !

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +15 Vote: I do not like it

That is an interesting problem. However I suspect that it might be not possible to solve it in O(n·polylog(n)).

Name our problem as A and we will introduce new problem B: Let a0, a1, ... , an and b0, b1, ... , bn be two sequences. Find sequence c0, c1, ... , cn such that ck = max(ai + bk - i).

It can be seen that if we are able to solve B in O(f(n)) times then we are able to solve A in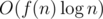 using divide and conquer (ai stands for a suffix of length i of first half and bi stands for a prefix of second half). Also, if we are able to solve A in O(f(n)) then we can solve B in O(f(n)) time by considering an array with very big element in a middle of it and every maximum subarray will contain it and we just have to choose how long suffix of first half it needs to contain. So in fact these two problems are equivalent in a meaning that if one has solution O(npolylog(n)) then second one also has it (or we can replace it with O(n2 - ε).

Also observe that we can replace ai with 2ai, so instead of maximixing sums we can maximize products. And problem looking like this already appeared on codeforces: 444B - DZY Loves FFT. But this problem was much easier than one we want to, because there one sequence was permutation, other one consisted of zeros and ones only and input was randomly sorted which allowed us to use some Las Vegas algorithm. Nobody seems to came up with solutions in more general case, so if it is not impossible to solve it then it is at least very hard.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    It seems that the problem B is solvable in O(n log n) expected time.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That is a nice result :). However it assumes that all permutations of those sequences are equiprobable which is usually not true for prefix/suffix sums which I applied in reduction. Moreover if elements in problem A are positive then those sequences are increasing and presented algorithm TACU will most likely run in O(n2). We can subtract mean of all elements to make it zero-sum (sequence from original problem A), which will very likely make it much faster, but I guess it will still be expected O(n2).

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Unfortunately, by the "expected time" they mean only that the average number of iterations over some general set of pairs of sequences has order 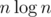. This doesn't really imply anything :(

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    sorry i understood it in a wrong way ... i understood that we need the max sum subarray of any possible length

    → Reply