Given a Matrix n*n size Let the matrix is A .. Now i have to find out.. A+A^1+A^2+A^3+.......+A^k(k=10^9).. i only can find out the A^k using matrix exponentiation... how can i find the solution of the above equation..
EXAMPLE:
n=3,k= 2
1 4 6
A=6 5 2
1 2 3
output:
208
484
722
problem link:http://lightoj.com/volume_showproblem.php?problem=1142










This was discussed many times already: A + A2 + A3 + ... + A2n = (I + AN)(A + A2 + A3 + ... + AN)
When n is odd you just find An and get again to the case when n is even.
You need to calc A^n each time. You may use formulas that doesn't require it
(I + A)(I + A2 + (A2)2 + (A2)3 + ... + (A2)n) for odd.
I + A(I + A + A2 + A3 + ... + An - 1) for even
Oh, that's a better approach. Nice.
Here is another way to calculate that power-sum. Build a new 2n × 2n matrix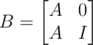 . Taking B to the kth power gives
. Taking B to the kth power gives 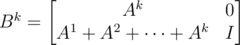 . This is easy to prove by induction.
. This is easy to prove by induction.
To solve the problem, I use classical matrix exponentiation to the following recurrences:
f(0)=A, f(n)=A*f(n-1)g(0)=O, g(n)=g(n-1)+f(n-1)This is my code, maybe this help you.