UPD Editorial of problem E was added, I apologize for the delay. Hope you found it interesting.
A. Face Detection
Author: Monyura
One should iterate through each 2x2 square and check if it is possible to rearrange letters in such way they they form the word "face". It could be done i.e. by sorting all letters from the square in alphabetic order and comparing the result with the word "acef"(sorted letters of word "face").
B. Looksery Party
Author: Igor_Kudryashov
In any cases there is such set of people that if they come on party and send messages to their contacts then each employee receives the number of messages that is different from what Igor pointed. Let's show how to build such set. There are 2 cases.
There are no zeros among Igor's numbers. So if nobody comes on party then each employee receives 0 messages and, therefore, the desired set is empty.
There is at least one zero. Suppose Igor thinks that i-th employee will receive 0 messages. Then we should add i-th employee in the desired set. He will send messages to his contacts and will receive 1 message from himself. If we add other employees in the desired set then the number of messages that i-th employee will receive will not decrease so we can remove him from considering. Igor pointed some numbers for people from contact list of i-th employee and because they have already received one message we need to decrease these numbers by one. After that we can consider the same problem but with number of employees equals to n - 1. If the remaining number of employees is equal to 0 then the desired set is built.
C. The Game Of Parity
Author: olpetOdessaONU
If n = k no moves may be done. The winner is determined with starting parity of citizens' number. Otherwise let's see that the player making the last move may guarantee his victory, if there are both odd and even cities when he makes the move. He just selects the city of which parity he should burn to obtain required parity. So, his enemy's target is to destroy all the cities of some one type. Sometimes the type does matter, sometimes doesn't. It depends on the player's name and the parity of k. So the problem's solution consists in checking if "non-last" player's moves number (n - k) / 2 is enough to destroy all the odd or even cities. If Stannis makes the last move and k is even, Daenerys should burn all the odd or all the even cities. If k is odd, Daenerys should burn all the odd cities. If Daenerys makes the last move and k is even, Stannis has no chance to win. If k is odd, Stannis should burn all the even cities.
D. Haar Features
Author: Monyura
This problem had a complicated statement but it is very similar to the real description of the features. Assume that we have a solution. It means we have a sequence of prefix-rectangles and coefficients to multiply. We can sort that sequence by the bottom-right corner of the rectangle and feature's value wouldn't be changed. Now we could apply our operations from the last one to the first. To calculate the minimum number of operations we will iterate through each pixel starting from the bottom-right in any of the column-major or raw-major order. For each pixel we will maintain the coefficient with which it appears in the feature's value. Initially it is 0 for all. If the coefficient of the current cell is not equal to + 1 for W and - 1 for B we increment the required amount of operations. Now we should make coefficient to have a proper value. Assume that it has to be X( - 1 or + 1 depends on the color) but current coefficient of this pixel is C. Then we should anyway add this pixel's value to the feature's value with the coefficient X - C. But the only way to add this pixel's value now(after skipping all pixels that have not smaller index of both row and column) is to get sum on the prefix rectangle with the bottom-left corner in this pixel. Doing this addition we also add X - C to the coefficient of all pixels in prefix-rectangle. This solution could be implemented as I describe above in O(n2m2) or O(nm).
Also I want to notice that in real Haar-like features one applies them not to the whole image but to the part of the image. Anyway, the minimum amount of operations could be calculated in the same way.
E. Sasha Circle
Authors: Krasnokutskiy, 2222
Author's solution has complexity 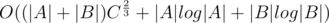 , where C is a maximum absolute value of the coordinates of all given points.
, where C is a maximum absolute value of the coordinates of all given points.
Let’s call a set of points A and B separable if there’s a circle inside or on the boundary of which lie all the points of one set. When there’re no points neither inside nor on the boundary of the circle we call this circle separating. Let points of the set A lie inside or on the boundary of the circle and points of the set B lie outside the circle. Points from set A are allowed to be on the boundary of the separative circle as after increasing radius a little we’re getting set A strictly inside and set B strictly outside the circle.
Let A contain at least two points. Separating circle can be compressed in such a way that it’ll pass at least through two points of the set A. It’s possible to look over all the pairs of points 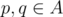 and try to pass each pair through the separating circle. The centre of the desired circle lies on the medial perpendicular of the segment pq. Let’s designate the points of the medial perpendicular as l(t) where
and try to pass each pair through the separating circle. The centre of the desired circle lies on the medial perpendicular of the segment pq. Let’s designate the points of the medial perpendicular as l(t) where 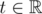 is a parameter. All the points that don’t lie on the straight line pq make parameter t bounded above or below. All the points that lie on the straight line pq have to lie outside the limits of the segment pq. E.g. a picture below displays a blue point which bounds the centre of separating circle from the left side and red points – from the right side. That’s why the centre has to lie inside a segment cd.
is a parameter. All the points that don’t lie on the straight line pq make parameter t bounded above or below. All the points that lie on the straight line pq have to lie outside the limits of the segment pq. E.g. a picture below displays a blue point which bounds the centre of separating circle from the left side and red points – from the right side. That’s why the centre has to lie inside a segment cd.
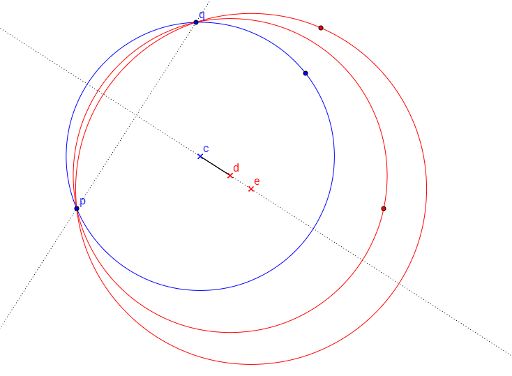
Let’s look over all the points to make sure that a value t which satisfies all the bounds exists. This provides us with the problem solving for O((|A|2 + |B|2)(|A| + |B|)).
Let’s examine paraboloid z = x2 + y2 and draw arbitrary non-vertical plane ax + by + z = c. The intersection of the paraboloid and the plane satysfies the equation ax + by + x2 + y2 = c, or 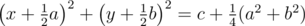 . If project points of the paraboloid (x, y, x2 + y2) onto the plane
. If project points of the paraboloid (x, y, x2 + y2) onto the plane 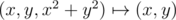 the cross-section of the paraboloid formed by the plane projects onto a circle, the paraboloid points below the plane projects onto internal points of the circle, those above the plane projects onto points outside the circle. As
the cross-section of the paraboloid formed by the plane projects onto a circle, the paraboloid points below the plane projects onto internal points of the circle, those above the plane projects onto points outside the circle. As 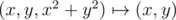 is one-to-one correspondence the opposite is also true: when points of the plane project onto the paraboloid
is one-to-one correspondence the opposite is also true: when points of the plane project onto the paraboloid 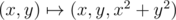 the plane projects onto the cross-section of the paraboloid formed by the plane, the internal points – onto the paraboloid below the cross-section and external points – above the cross-section.
the plane projects onto the cross-section of the paraboloid formed by the plane, the internal points – onto the paraboloid below the cross-section and external points – above the cross-section.
So, projection of points onto paraboloid assigns one-to-one correspondence between circles and planes (non-vertical). partitioning of sets of points A and B of plane by circle can be done by means of partitioning of their three-dimensional projections into paraboloid A′ and B′ by non-vertical plane. Let’s call such a plane separating (like separating circle, separating plane can include points from A′).
By analogy with separating, circle separating plane can be passed through two points of set A′. All the other points of A′ will lie below or on the plane. In other words separating plane will pass through the edge of the upper convex hull of the set A′. The projection of edges of the upper convex hull A′ onto the plane xOy will produce some sort of a set flat convex hull partitioning into A by non-intersecting edges. In this case separating plane corresponds separating circle passing through the edge partition. Let’s designate the convex hull A as coA. In case when none of 4 vertices coA lies within one circle all the edges of the upper convex hull are triangles and the derived partitioning is triangulation. Otherwise the derived partitioning should be completed to be triangulation.
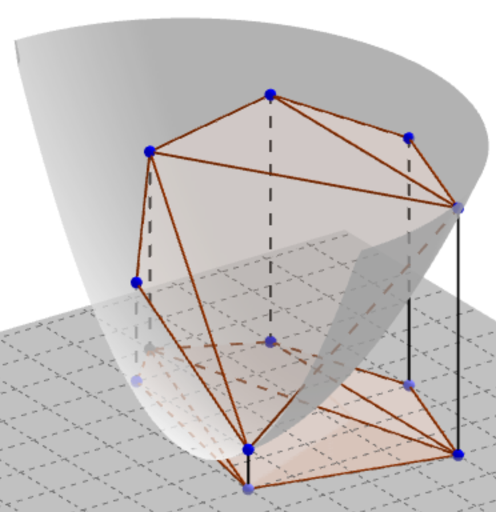
To construct a separating circle look over triangulation edges and check the possibility of drawing a circle though an edge as it is described above.
The derived triangulation has the following feature: circle drawn around any triangle contains the whole polygon coA as the corresponding bound of three-dimensional convex hull is higher than all three-dimensional points A′. The described triangulation is “opposite” to the Delaunay triangulation according to which circle drawn around any triangle doesn’t contain any points of the original set. This triangulation is commonly known as the Anti-Delaunay triangulation.
Using the characterizing feature the Anti-Delaunay triangulation can be constructed by means of the method “divide and conquer” without transferring into three-dimensional space and working with points of plane and circles only. Let us triangulate polygon created by the vertices coA when moving counter-clock-wise from i to j. Let us find the third point of triangle, that will contain edge (i, j). I.e such point k, that circumscribed circle over triangle (i, j, k) contains the whole current polygon. For this purpose let’s iterate through all polygon’s vertices and select the one, that gives the extreme position of the center of the circumscribed circle lied on the mid-perpendicular of (i, j). The circle will contain the whole polygon coA as the edge (i, j) is included in the Anti-Delaunay triangulation. Recursively triangulate polygons with vertices from i to k and from k to j. The base of recursion is a segment, that shouldn't be triangulated.
To solve the original problem one should swap A and B and perform the above procedure once more. Complexity of the algorithm is O(|A|log|A| + |coA|(|coA| + |B|) + |B|log|B| + |coB|(|coB| + |A|)=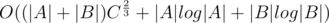 , where C is a maximum absolute value of the coordinates of all given points. Actually, O(C3 / 2) is an estimation of the number of points at a convex hull with no three points in a line.
, where C is a maximum absolute value of the coordinates of all given points. Actually, O(C3 / 2) is an estimation of the number of points at a convex hull with no three points in a line.
F. Yura and Developers
Authors: Rubanenko
Let's consider following solution:
Let f(l, r) be the solution for [l, r] subarray. It's easy to see that f(1, n) is the answer for the given problem. How should one count f(l, r)? Let m be an index of the maximum value over subarray [l, r]. All the good segments can be divided into two non-intersecting sets: those that contain m and those that don't. To count the latter we can call f(l, m - 1) and f(m + 1, r). We are left with counting the number of subarrays that contain m, i.e. the number of pairs (i, j) such that l ≤ i < m < j ≤ r and g(i, m - 1) + g(m + 1, j)%k = 0 (g(s, t) defines as + as + 1 + ... + at). Let s be the sequence of partial sums of the given array, i.e. si = a1 + a2 + ... + ai. For every j we are interested in the number of such i that sj - si - am%k = 0, so if we iterate over every possible j, then we are interested in number of i that si = sj - am(modk) and l ≤ i < m. So we are left with simple query over the segment problem of form "how many numbers equal to x and belong to a given segment (l, r)". It can be done in O(q + k) time and memory, where q is the number of generated queries. Model solution processes all the queries in offline mode, using frequency array.
One can notice that in the worst case we can generate O(n2) queries which doesn't fit into TL or ML. However, we can choose which is faster: iterate over all possible j or i. In both cases we get an easy congruence which ends up as a query described above. If we iterate only over the smaller segment, every time we "look at" the element w it moves to a smaller segment which is at least two times smaller than the previous one. So, every element will end up in 1-element length segment where recursion will meet it's base in O(log(n)) "looking at" this element.
The overall complexity is O(n × log(n) + k).
G. Happy Line
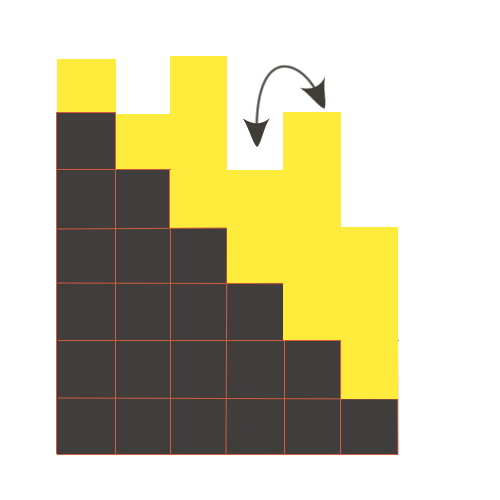
Let's reformulate the condition in terms of a certain height the towers, which will be on the stairs. Then an appropriate amount of money of a person in the queue is equal to the height of the tower with the height of the step at which the tower stands. And the process of moving in the queue will be equivalent to raising a tower on the top step, and the one in whose place it came up — down. As shown in the illustrations. Then, it becomes apparent that to make all of the tower on the steps to be sorted, it is enough to sort the tower without the height of step it stays. Total complexity of sorting is O(nlog(n)).

H. Degenerate Matrix
Author: Igor_Kudryashov
The rows of degenerate matrix are linear dependent so the matrix B can be written in the following way:
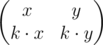
Suppose

Let's assume that elements of the first row of matrix A are coordinates of point a0 on two-dimensional plane and the elements of the second row are coordinates of point a1. Assume that the rows of matrix B are also coordinates of points b0 and b1. Let's note that in this case the line that is passing through points b0 and b1 is also passing through point (0, 0).
Let's find the answer — the number d — by using binary search. Suppose we are considering some number d0. We need to check if there is such matrix B that

In geometric interpretation it means that point b0 are inside the square which center is point a0 and length of side is 2·d0. In the same way the point b1 are inside the square which center is point a1 and length of side is 2·d0. So we need to check if there is a line that is passing through point (0, 0) and is crossing these squares. In order to do this we should consider every vertex of the first square, build the line that is passing through the chosen vertex and the center of coordinate plane and check if it cross any side of the other square. Afterwards we should swap the squares and check again. Finally if there is a desired line we need to reduce the search area and to expand otherwise.










I still don't know what problem D was asking for. What is this value, why are we multiplying etc Can someone please clarify?
You have an n*m matrix initially containing zeroes. You have a pattern of W's and B's, and want to transform the matrix such that it has a 1 where the pattern has a W, and a -1 where the pattern has a B. The only allowed operation is "add k to each position in this rectangle whose topleft is the topleft of the matrix, for some integer k". What is the minimum nummer of operations?
How on earth did you unravel this enigma? Thanks a lot though!
Jeez! Thanks for clarification. I would have had more chance understanding the problem without reading the problem statement :/
E. Sasha Circle
Authors: Krasnokutskiy, 2222
Coming soon???
Am I the only one who found it impossible to understand problem D's statement?
No No No No
I was going to abondon it at some time (especially the first time I read it)
of course NO!
In my opinion, it is good example, when easy problem complicated an incomprehensible statement to make this problem more difficult.
I thought D's statement was straightforward. I suspect the confusing aspect for all of those who found it incomprehensible was the gap between face detection and Haar features, i.e. why would we want to compute such features. Maybe once we lose the thread of motivation, things become harder to understand?
I wanted to describe the Haar features usage at a face detection but then look at the amount of text :)
Yes, peer review sometimes mutilates a problem's enlightenment potential. But well done for trying to teach Viola-Jones to 5000 people! (Worked for me, by the way. Now I know more than just the famous name.)
Don't read this xd
k = 106
Omg, I'm such a moron >_>
I was reading problem D. When I perfectly understood problem D, I found that contest is over.
I can't open the problemset... Any ideas why, it shouldn't be blocked anymore, right?
On problem B, I believed that by
it was meant that
because of my distrust in English statements of contests made by Russian-speaking guys. :/
In Problem C,
Shouldn't this be
yes, you're correct. there is an error in the editorial.
Fixed, thank you!
Problem H could be solved in O(1) without any binary search. Consider the case when a, b, c, d ≥ 0. Then define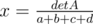 . One may note,
. One may note,
Take B as the above matrix. Then the answer in this case equals |x|. (But we strictly proved only that answer $\leq x$ ).
If some of a, b, c, d are negative, this also holds, but better answer exist. We wanna get |a| + |b| + |c| + |d| in the denominator of x. One may note that if we have an even number of negative elements, it is possible to use the same B matrix, but reverse somewhere signs for x'es (and get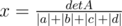 , and |x| as an answer). For example, if a < 0 and c < 0, we take
, and |x| as an answer). For example, if a < 0 and c < 0, we take
Only essential case is if we have an odd number of negative elements in initial matrix. Then we have to subtract minimal element of (|a|, |b|, |c|, |d|) instead of adding, and answer equals
However, I was unable to prove the minimality of x chosen this way during the contest (but solution got AC). Any ideas?
Hey! Really nice idea. :)
How did you come up with such an idea in the very beginning?
I found this code in the announcement page. Is this same as yours? Though it seems different. http://codeforces.net/contest/549/submission/11467650
You can come up with such an idea when you see at example tests. Futhermore, this idea is similiar to Equioscillation theorem (http://en.wikipedia.org/wiki/Equioscillation_theorem) from numerical analysis, which is used to finding polynomial of bounded degree, that maximal absolute value of difference between given function and this polynomial is as smallest as possible. This helped me with coming up with similiar idea.
this idea is really fantastic! sadly i failed to deal with the negative elements...
math is awesome
My approach was similar. I proved it using contradiction which I hope is correct. Let the optimal solution be x and x ≠ xd. Thus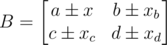 (It doesn't matter where we put x due to symmetry).
(It doesn't matter where we put x due to symmetry).
Since det(B) = 0, (a ± x)(d ± xd) = z1 . I won't make it lengthy, but it can be easily proved that there is an optimal mid value xd < x' < x which can replace both x and xd, contradicting the optimal solution x itself. Similarly we can assume xb = xc. Moving on, again assume x to be the optimal answer.
How can Problem D can be implemented in O(n,m)?Can someone please explain?
Check 11483301.
Create an array b, such that b[i][j] = 1 if (i, j) is white and b[i][j] = - 1 if (i, j) is black.
Keep a counter for the answer. For every (i, j), we want to determine if we need a rectangle whose bottom-right vertice is (i, j). The rectangles (except the one whose bottom-right vertex is (i, j)) containing (i, j) must also contains (i + 1, j) or (i, j + 1), so the sum of those rectangles' values is b[i + 1][j] + b[i][j + 1]. But, we will count some rectangles twice, those containing both (i + 1, j) and (i, j + 1), which must contain (i + 1, j + 1)! So, the effect of previous rectangles on (i, j) is b[i + 1][j] + b[i][j + 1] - b[i + 1][j + 1]. If this value doesn't equal b[i][j], we'll need another rectangle whose bottom-right corner is (i, j), so we increment the counter.
Cool trick,definitely going to remember this.Thanks johnathan
I don't get it. Could somebody explain it in other words (maybe even with pictures)? :)
My understanding of this problem might be wrong, but let me try. We will start operations from rectangle (0, 0, n, m). This way we satisfy at least point (n, m), forget about it and move on. Now all array is filled with -1's or 1's. Find next point that is not ok and do operation again. Now, for every point (i, j), how will all bigger rectangles (0, 0, i+a, j+b) effect it? Effect is b[i+1] + b[i][j+1] — b[i+1][j+1]. By effect I mean this. If we want to satisfy point (x, y) we add some value to all rectangle (0, 0, x, y). This effects points (0, 0), (0, 1), (1, 0), (1, 1) and so on to point (x, y). Hope I got it right and my explanation is not misleading :)
Be careful, this is not always possible (if the top row is 0).
Then we will not write 0,0 in the top row. Suppose the 2 points are (0,0) and (6,5). We will write in the following way.
Edit: Oh..u r right...The one with the (0,0) in top row is also degenerate but cannot be written in that form.
ad-bc=0. => ad=bc => b/a=d/c = t (problem is here. if a=0 or c=0. Then we cannot write like this) => b=at and d=ct.
in problem B, in the second case,
solution said: Suppose Igor thinks that i-th employee will receive 0 messages. Then we should add i-th employee in the desired set.
why we should add i-th employee? maybe we don't add i-th employee and we add someone else that messages him.
You forgot that every employee is messaging himself.
No, DartJaf means why i-th employee MUST be selected. Think of the case: 110 010 011
You can select 1th and 3rd employee to send 2 messages to 2nd employee.
i got it!
with the strategy that explained in the solution we can solve any input and there is no "no solution"! if for some input this method dose not give us a solution then we can ask: why you choose i-th people while you have other choice.
so this should is different from that should!!
i had the same doubt as you did, but your words inspired me a lot!
since there's N+1 possible value for A_i, but only N employees in total. so with the method mentioned above there's always a solution to the problem! so we don't have to consider other ways to construct but just to select the point itself is OK!
Problem H, suppose we use binary search to check answer d. Let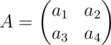 .
.
We want to check if there exists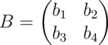 , such that |bi - ai| ≤ d and b1b4 = b2b3.
, such that |bi - ai| ≤ d and b1b4 = b2b3.
Since a1 - d ≤ b1 ≤ a1 + d and a4 - d ≤ b4 ≤ a4 + d,
we have min(S) ≤ b1b4 ≤ max(S).
where set S = {(a1 - d)(a4 - d), (a1 - d)(a4 + d), (a1 + d)(a4 - d), (a1 + d)(a4 + d)}.
Similarly, we can calculate the upper and lower bounds of b2b3.
If the range of b1b4 and b2b3 intersect, d is a possible answer; otherwise not.
Your explanation is so helpful! Thank you! And I saw someone use another way to solve problem H, just like this. I have difficulty proving its correctness. Please help me!
below is some part of your solution can you please tell me logic behind this..
REP(i, 10000) { double m = (lb + ub) / 2; auto p1 = mm(a, d, m); auto p2 = mm(b, c, m); if (p1.second < p2.first || p2.second < p1.first) { lb = m; } else { ub = m; } }
It's just binary search.
-
lb: current lower bound-
ub: current upper bound-
m: mid-point of the two bounds, corresponds to d in my previous explanation-
mm: a function returning the ranges of a * d and b * cIf those ranges don't intersect, then m is not large enough, let lower bound = m; otherwise m is large enough, let upperbound = m
your solution is awesome but why did you looped till 10000 in ur solution ?
I see most people use 100 times only. But I thought 10000 should also fit the time limit easily.
You could also stop when the difference between upper and lower bounds is less than 10 - 6.
can someone explain solution of problem H by binary search.
I hope my comment above is helpful.
Does anyone know how to avoid getting WA on Pretest 10 on Problem E?
I cannot understand why and how the solution of problem G is working. Can anyone explain more? :|
We have an array of persons (we will call it persons, persons[n - 1] — the head, persons[0] — the tail). For each person we will calculate this number val = money of a person — (number of steps to reach the head of the queue). Next we sort persons by val.
Suppose there is an answer ans. (ans[0] — the tail, ans[n - 1] — the head). ans[i].money — how much money is left with ith person in ans.
persons[n - 1].val ≥ ans[n - 1].money, so we can transform the answer so that persons[n - 1] is in the head.
persons[n - 2].val + 1 ≥ ans[n - 2].money, so again we can transform the answer. Why val + 1? Because we need to get to n - 2, no to n - 1.
Then persons[i].val + (n - i - 1) ≥ ans[i].money. So you can put persons[i] in the ans on ith position with money persons[i].val + (n - i - 1).
Excuse me for my mistakes.
http://codeforces.net/contest/549/submission/11481852
P.S. If we want to move a person to a specific position, then no matter which steps we take, the person will be left with the same amount of money. I think that's the main observation.
Hi dears The contest was not bad,but question D has been translate to English very badly...!
I have to read problem D for more than 15 times :D
Lol :D. I thought it happend just for me :D
For problem C I am thinking in a greedy manner . Initially I can find whether my total sum is even or odd store the parity in a variable sum and accordingly maintain two variables which would store count of even and odd numbers present . Now say the player A wins when the total sum of remaining cities is odd and B wins when the total sum is even. When looping through N-K(Number of cities to destroy) if parity of my sum is even then A would try to take an odd number in doing so count of odd number would be decreased and parity of my sum would be flipped and accordingly B would also approach in a similar manner . If at any time in between the loop if count of a variable goes to 0 then other player wins else after the loop has completed we check the sum variable if it is 1 A wins and if 0 B wins . Is this intuition right ?
This statement is already incorrect. If the count of a variable goes to 0, then the game is fully determined afterwards, but it's not true that the other player wins. (For example, if Daenerys destroys the last odd city, then Daenerys is the winner, not Stannis.)
I did not understand one bit, the explanation for problem G. Can someone please explain a little more clearly? Thanks
Nor did I ...
I had to read some solutions from some top coders to figure it out on my own.
Denote A[i] as the money of the ith person standing in the queue. First realize that the coin difference after performing a number of swaps ultimately depends on the absolute displacement of each person. In other words, if a person was at position i, their position changed to j, and they had c money initially, then their new amount would be c + (i - j).
So instead of performing the +1 and -1 operations we will increase the money of each person standing at i by i, i.e., A[i]: = A[i] + i. After we performed some swaps, we then subtract the money of the person standing at j by j, i.e., A[j]: = A[j] - j. This is equivalent to gaining i - j units at the end.
Now, after we increased every A[i], we must sort the array, and we must check if A[i] is strictly increasing because if A[i] = A[i + 1], then A[i] - i > A[i + 1] - (i + 1), and this would mean, we failed our original goal.
That made it very clear, thanks a lot :)
Just to add a final bit to your nice explanation:
Why we sort after adding i to every A[i]?
Ans: Consider a permutation of the A[i] + i different from the sorted order and now subtract j from A[j]. Now some consecutive pair of elements exists such that A[j] > A[j + 1]. The equality A[j] - j ≤ A[j + 1] - (j + 1) should hold. Which cannot hold if A[j] > A[j + 1]. Hence, we need to sort.
That's cool. But how could someone possibly come up with the idea of those towers and stairs of the tutorial or adding i to A[i]? Pretty much 'bolt from the blue'. :P
On a serious note, how to actually come up with such an idea?
Indeed, I think that solving this problem is much easier than understanding this explanation xD. Just note that money+position is an invariant for each person and there's nothing left to be done here.
I don't quite get your point — It's an invariant... so what?
Sooo, if rightmost man needs to have largest amount of money then he needs to have largest value of (money+position) and so on, so we need to sort them by that invariant and check if that's a valid arrangement.
Nice Swistakk! Something to add to the arsenal of solving techniques:
Find an invariant. Establish a realtion to the problem.
Lots of physics problems are solved that way.
Thanks for appreciation, but keep in mind that my thought process was not like "Let's find an invariant! Hmm, money-position doesn't work, money*position also, oh, money+position works!" rather "Hmmm... If guy walks one unit to right he loses one coin and if he walks one unit to left he gains one coin, so money+position is invariant!"
Thanks for showing your thought process.
Here's ITDOI's solution for H that is O(1) : 11490362
It is based on the guess that there is one desired matrix B, which entries of matrix A-B have equal absolute values! (like two sample tests)
Can anyone prove it please?
looking for proofs too
I made almost the same thing.The idea is that when you are binary searching, you obtains 2 intervals which have to intersect.if x is bigger, the intersection is bigger, and you want the smallest x, so the intersection must be exactly one point.For that, left part of the first interval must be equal to the right one of the other, and the limit cases are obtain using a difference equal to either -x, either x.In my solution I fixed the signs of difference for each cell, but is still O(1)
Generally I can prove it in a way acceptable to some people, but not really formal:
Suppose
where |a| < |b|. We'll prove that such B cannot be optimal.
Let's apply some small variation to matrix B:
where δ has the same sign as b. Then if |δ| is small enough then norm of A - B' will be |b - δ| which is obviously less than |b|. QED.
I'm not buying it. What if number of entries with biggest absolute value is bigger than 1 and less than 4? There are lots of such cases.
Ok, this is what will work in more generic case:
Worst case you have 3 biggest values (let's say all except bottom right). Then let's say,
and the signs are chosen in such way that the absolute value of corresponding elements in A - B are improved. Then can be determined in such way that
can be determined in such way that 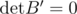 .
.
so you say that this code should not be accept?!
No, on the contrary I actually claim it's possible to prove this approach.
thanks
If we see A as two vectors, then adding B is like adding a couple of parallel vectors of possibly different lengths to these two column vectors of A (because B is degenerate). So we can slide these two column vectors on parallel rails in a direction and by distances that we choose. Now, if there is a line in 2D, I think it's easy to see that the point on the line that is nearest the origin, in the Manhattan metric, is going to always lie on the corner of some axis-aligned square centred on the origin. (In other words, either on the line x = y or x = -y.) So we have two such squares for some choice of B, and they must be of equal size, because otherwise we would rotate the line of B to reduce the size of the larger one (we can always do that because for some choice of B it goes to zero). There is always a solution for which the column vectors of A-B are opposite corners of such a square. (Which, by the way, means that A-B is also degenerate.)
Thanks, now it's been clear for me ;)
wonder why is problem E's still coming soon?
just cant wait XD
why was i getting downvote?
anyone please tell me why?
really that comment was before the update of the tutorial....
I dont know if someone already realized that and discussed here, but the editorial for C is wrong when says: "If Stannis makes the last move and k is odd, Daenerys should burn all the odd or all the even cities...", the correct is even.
sorry for my bad english, and please correct me if I'm wrong or i misunderstood the editorial.
This might be useful for Smallest enclosing circle
For problem E can it not be done by finding out convex hull for one set of points then find two most distant points on the boundary of convex hull, with the mid-point between these two points as center and half of distance as radius we can create a circle covering all the set-one points. Next we can check one by one for the points from other set if they lie outside the circle.
First of all, the circle that you described won't necessarily contain all the points from the convex hull, for example : (0, 0), (1, - 2), (4, 0), (1, 2). And even if it does, the circle could contain also some points from another set so it couldn't be taken as an answer, but answer could exist.
For problem E, why finding out the smallest enclose circle and check if there's one point from the other set in the circle to decide the answer can't be accepted?
Here's a counterexample: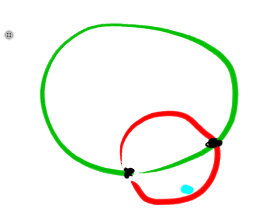 The red circle doesn't work, but the green circle splits the black and blue points. EDIT: To strengthen the counterexample, add another blue point somewhere above the diagram.
The red circle doesn't work, but the green circle splits the black and blue points. EDIT: To strengthen the counterexample, add another blue point somewhere above the diagram.
tourist solved 549D - Haar Features using BigInteger in java. submission : 11464258 He might think the difference that should applied to the image increases exponentially. Can anyone explain how the maximum difference increases according to N?
In problem B, why choosing the position with zero requirement is optimal? Why not someone who can message him?
We want to guarantee that already picked people got more than a[i] messages. If the next person to pick got less than a[i] messages then there is no guarantee that the person will have got the number of messages not equal to a[i] by the end. But.. If you pick a person which got a[i] messages, then he will get +1 from himself. So, we satisfied the requirement that "already picked people got more than a[i] messages". If there is no person which got a[i] messages, then we should not invite them to the party.
I am asking why a solution is not possible by taking someone who sends the guy a message if we do not get a solution by taking the sane guy?
In problem F , how do we find number of occurrences of a number of O(Q + K) time ? , i used a vector and lower_bound but in worst case its (Q * log(N)) . How to do it in O(Q + K) time ?
If you have queries like how many times S[pos] = val with L <= pos <= R (So you have parameters L, R and val), you cand count how many times you have S[pos] = val with pos <= R and than subtract the number of position pos such that S[pos] = val ans pos < L. This way you have just queries like how many values equal to val are on some prefix. You can keep some STL vector, storing in v[i] all val of all the queries on prefix i. Now you can just iterate with i from 1 to N and at this step process the queries on prefix i (keep in parallel a frequency array). Here is my source: http://codeforces.net/contest/549/submission/12921309 .Look at fucntion add_query and at the end where ai process the queries for better understanding
why these two images from the last problem dose not appear well?!
I tried many browsers and none of them showed these images!!
would anyone please explain this method for solving 549H - Degenerate Matrix
Pictures for H are 404'ing... maybe Monyura or someone else can reupload them?
E is much harder than a 2700 problem, even tourist didn't solve it during contest. Why is it rated only 2700?