keyvankhademi's blog

Project Euler Problem #511
By keyvankhademi, 10 years ago, In English

Recently i was trying to solve some Project Euler question. Then i met problem #511 in which i interested a lot.
I want to share the problem and my solution with you. Here it the link to the problem.

The Problem:

let define seq(n, k) number of sequences a1...an which has this two property.
1) n is divisible by ai
2) n + a1 + a2 + ... + an is divisible by k

Two numbers n ans k are given, output seq(n, k) mod M
you may consider n <  = 1012 and k <  = 5000

Solution:

My solution idea came from this blog. Thanks from kien_coi_1997.
Consider dp(m, rem) which mean the answer to the problem if the the sequence size is m and sum of numbers in sequence is rem mod M.
You can recursively call function dp. consider m is odd then you can brute force a1 and find the rest with dp(m - 1, rem - ai). and if m was even you can split the sequence in to two equal sized sub-sequence. By brute forcing the sum of the first sub-sequence you can find the answer with dp(m / 2, r1) * dp(m / 2, rem - r1) .

long long dp(long long m, long long rem)
{
    long long ans = 0;
    if(m&1)
    {
	for(int i = 0; i < dv.size(); i++)
	{
	    ans += dp(m-1, ( rem - dv[i] + k )%k );
	}
    }
    else
    {
	for(int i = 0; i < k; i++)
	{
	    ans += dp(m/2, i)*dp(m/2, (rem - i + k)%k );
	}
    }
    return ans;
}

Then you can call function dp(n,  - n) as the answer for the problem.
The time complexity of this solution is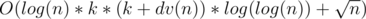
which dv(n) is number of divisors of n and log(log(n)) is because we should memoized with map
Although this solution is not very efficient but it was enough for PE, any faster solution will be appreciate.

UPD: With optimization we can reach time complexity.

  • Vote: I like it
  • +18
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Discussing PE problems publicly is usually frowned upon (there is after all a forums thread for the problem available to those who have solved the problem), but it is indeed an interesting problem so whatever (and you've already made a feasible solution public so...). =D

  • First of all, you're only interested in the value of the divisors mod k, i.e. you can count for each residue value how many divisors/numbers there are. This helps you get rid of the dv(n) factor.
  • You don't need a map, an ordinary matrix will do. Just index it by the recursion depth (which is bounded by ) and the remainder.
  • Using these two ideas you'll get a solution, disregarding the time taken to calculate the divisors of n.
  • Once you've coded this solution it's quite obvious that each dp-level in the recursion is just a result of the circular discrete convolution of the previous one with either itself (even case) or the count array for divisors (odd case). And the circular discrete convolution can be calculated with FFT, so in total we get .
→ Reply
»
10 years ago, # |
  Vote: I like it +23 Vote: I do not like it

It is bad idea to discuss new projecteuler problems.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I Know, but it is not a recent problem of PE. so it has no effect on PE's rating.
    And the reason that i post it here was that i wanted others try to solve this beautiful question and then see others solution.

    → Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

In order to clarify my solution above a little bit, I've implemented basically the same idea but using Karatsuba instead of FFT, which yields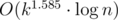 complexity disregarding the initial computation of the divisors.

Code: Reduction to Karatsuba

This solution reduces the problem to polynomial multiplication, and uses the trick that the range [k, 2k) of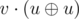 (where denotes concatenation) corresponds to the circular discrete convolution of v and u.

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

Another idea of this problem:

If you get recursion formula of dynamic programming, and then write it in the matrix form, one will notice that the matrix is a circulant matrix. The circulant matrix has some interesting properties, forms a cyclic group of order K. So similar to the polynomial multiplication, we can reduce the complexity of matrix multiplication to O(K2), or O(KlogK) through FFT.

→ Reply