Given the area of 3 triangles S1, S2 and S3 as shown in figure. 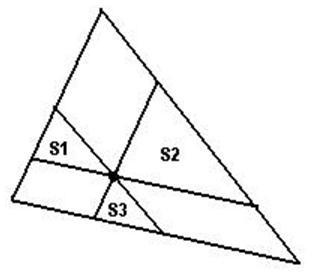
How to find the area of large triangle. ?
For example — if areas given are S1 = 1.0, S2 = 2.0 AND S3 = 3.0
Then Area of large Triangle = 17.19150823
I got this problem on link
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
Given the area of 3 triangles S1, S2 and S3 as shown in figure. 
How to find the area of large triangle. ?
For example — if areas given are S1 = 1.0, S2 = 2.0 AND S3 = 3.0
Then Area of large Triangle = 17.19150823
I got this problem on link
| Name |
|---|



Hint: Try to find area of 'medium' triangles. Use the similarity of triangles.
Short answer:
Explanation:
First of all, the three triangles are similar to each other, and similar to the big triangle. Every two smaller triangles are also similar to a bigger triangle that encloses them (for example, see the enclosing triangle of the triangles S1 and S3). These three enclosing triangles are similar to the big triangle. We know that if two triangles are similar, then the ratio of similarity is equal to the square root of the ratio of their areas. We also know that . Knowing these, we can compute the area of the triangle which encloses S1 and S3. Let L1, L3 be the lengths of the left sides for triangles S1 and S3 respectively. We know that the ratio of similarity of S1 and S3 is
. Knowing these, we can compute the area of the triangle which encloses S1 and S3. Let L1, L3 be the lengths of the left sides for triangles S1 and S3 respectively. We know that the ratio of similarity of S1 and S3 is  . We can see that λ2 = L1 / (L1 + L3) is the ratio of similarity of the triangles S1 and S1,3 (S1,3 is the triangle enclosing S1 and S3). So, now we can find the area of S1,3, which is
. We can see that λ2 = L1 / (L1 + L3) is the ratio of similarity of the triangles S1 and S1,3 (S1,3 is the triangle enclosing S1 and S3). So, now we can find the area of S1,3, which is  . In the same manner, we can find S1,2 and S2,3. We add them all together and subtract the parts that are counted twice, which are the triangles S1, S2 and S3.
. In the same manner, we can find S1,2 and S2,3. We add them all together and subtract the parts that are counted twice, which are the triangles S1, S2 and S3.
Sorry for the numerous revisions on my comment, but I am not very familiar with latex.
Answer is :
(sqrt(S1)+sqrt(S2)+sqrt(S3))^2