In how many ways can you tile a 2 * n rectangle with triominoes? A triomino is a geometric shape made from three squares joined along complete edges. There are only two possible triominoes:
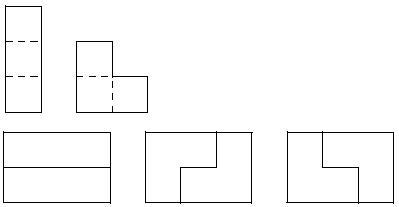
For example, you can tile a 2 * 3 rectangle only in 3 different ways. As the answer can be quite big, you just need to find the number of ways modulo 106.
Constraints : Number of test cases t (1≤t≤100). Each of the following t lines contains the value of n(0 < n < 109).
Output : Answer modulo 106.










Matrix exponentiation.
Let's consider all the states we can reach from a state x where x can equal (00, 01, 10) first bit stands for the up cell and the second bit for the bottom cell.
Now for example for state 00 and column i
F(i, 00) - > F(i + 1, 01)||F(i + 1, 10)||F(i + 3, 00)
Now we can make a transition matrix and raise it to power n.
Not getting the idea what exactly this states 00, 01, and 10 means with respect to problem?
It's a bitmask means that in the i-th column the first row was occupied or not (first bit) and the second bit for the second row likewise.
3^(n/3) if 3 divides n, 0 otherwise.
I'm assuming you got this from treating each group of 3 columns independently, since each such group can be filled in any of the following ways:
111
222
112
122
122
112
However, this misses tilings such as this one:
122233
114443
First you need to get a recurrence relation for the answer. There are several ways, like the one described by RetiredAmrMahmoud, here is a bit different approach:
Let the answer be an, and the number of tilings of 2 × n rectangle without a single corner cell is bn. Notice, that on the left side of 2 × n rectangle can be either two horizontal I-triominoes, or one L-triomino with its corner up or down (i.e. L or Г). It gives the following relation: an = an - 3 + 2bn - 1. Similarly, bn = an - 2 + bn - 3. It's enough for getting a solution, but substituting one into another we can get a simpler relation: an = 4an - 3 - an - 6.
Now, the usual way is to use matrix exponentiation, but this problem can be solved even if you don't know about it. The recurrence above modulo 106 has a small period (I think less than 107), so you just need to precalculate answers in that period.
AFAIR the problem was used in the ACM ICPC Quarterfinal in Ukraine in 2009, and several teams used the latter approach.
Can you explain a bit how come this recurrence formed bn = an - 2 + bn - 3 I think, it should be bn = an - 2 + bn - 1. I got this difference while generating recurrence by myself.
On the side of 2 × n rectangle without a corner cell there is either L-triomino (an - 2), or two I-triominoes (bn - 3).
Looking at the first recurrence an = an - 3 + 2bn - 1, Say n = 3, we have
a3 = a0 + 2b2
a3 = 1 + 2 * 0 ..... since a0 = 1&b2 = 0
a3 = 1
But there are 3 different ways.
b2 = 1, containing a single L-triomino. Here are a few first values:
Nice one. I have seen recurrence problems solved this way.
What can be a generalized approach to solve this kind of problems?