Since the possible mods are limited, if we used 4 numbers for example and our current modulo is 3 ,and another permutation of those 4 numbers gives also modulo 3, in the naive solution if we have 18 digits we would try the left 14 digit permutations twice, but the answer of this subproblem is saved in the DP table you don't have to recalculate it , you just add the numbers as you calculated them before!, So the complexity is cut to the number of subproblems you need to calculate!

First of all, the actual complexity is 2^N * M * N.

I'll try to explain why you don't need to go through all the permutations, then maybe the DP solution will start making sense. The key idea, like in every other DP problem, is that you don't need to know the exact intermediate state (in this case, the prefix of the permutation) to be able to compute the answer for the whole problem. Instead, you can define features of intermediate state that are important for your problem -- in this case, the subset of digits that have been used and the remainder modulo M that this prefix has. Two prefixes that consist of the same subset of digits and have the same remainder will "behave" in the same way with regard to the function you are trying to compute (i.e., the number of permutations that divide by M).

This probably didn't make so much sense to you, so let's look at an example. Suppose M = 7 and N = 1122334. Look at the following two prefixes, both comprised of (multi)set {1, 2, 2, 3, 3}: 31232 and 12332. They both have remainder 5 modulo M = 7. You obviously have the same set of numbers that can be appended to these prefixes. On the other hand, for any digit X, when you append it to either of this prefixes, the resulting remainder will be the same for both of them. For example X = 1: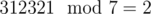 , 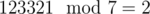. If this confuses you, think about the rules of how modulo operation behaves for multiplication: 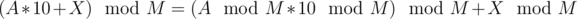, therefore the exact value of A does not matter, only 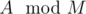does. Hence, you don't care any more if it was prefix 31232 or 12332 that you were trying to complete, the number of ways to complete it will be the same. This means that you could count how many prefixes are there comprised of {1, 2, 2, 3, 3} with remainder 5 modulo M and see in how many ways any of them can be completed and multiply these two numbers, instead of computing the number of ways to complete every one of these prefixes.

Hope this helps a bit.

You write: "For example, bitmask 0110 can be obtained as 0100 adding third digit to the end or 0010 adding second digit to the end." Now consider the next step: the bitmask 0111 can among others be obtained from 0110, and now your two ways of reaching 0110 are taken care of using one operation only.

It might help to look at the following somewhat silly DP to calculate the number of permutations:

dp[0] = 1;
for (int mask = 1; mask < (1 << N); mask++)
    for (int i = 0; i < N; i++)
         if (mask & (1 << i))
             dp[mask] += dp[mask ^ (1 << i)];

Here, dp[mask] is the number of ways to obtain mask, and dp[(1 << N) - 1] is of course N!.

in this comment it is well explained. however, this maybe a hard example for dp magic i suggest you to see this problem. it is somehow easier, at least no need to mask anything here. in short the problem states that you have(n <= 10000) number and (k <= 100) after you read this n numbers you have to say whether we can put operations between the numbers (+, -) that the final result will be divisible by k or not. as a naive solution we have (n-1) gabs between the numbers and we are to choose to put + or - this is 2^(n-1) possibilities! then for each possibility we calculate the result and see if it's divisible or not. However we can see that we are not interested in the final result, we are interested in its modulo on k, and from there we can see how dynamic programming will work just define state dp[i][j] = can we put operations between numbers (0 ... i) to reach modulo j on k, and the transition is simply dp[i][j] = dp[i-1][(j+A[i])%k] || dp[i-1][(j-A[i])%k], so we reduced O(2^(n-1)) to O(n*k) !

При добавлений новой цифры, как он изменит остаток?

remainder = (remainder * 10 + added) % mod

Значит, при добавлений новой цифры тебе важно только какие цифры до нее. Тебе не важно, в каком они порядке.

Can Anybody show me the whole procedure for following input?

Input: 123 3 Output: 6

Жыл один парень и однажды его сбила машина, ноги отказали и он не мог ходить(((( друзья помогали но потом перестали а девушка бросила... И вот он отчаялся и решил спрыгнуть из моста, но когда он уже свесился с перил какойто прохожий расказал ему про дп с битовыми масками.. парень не поверил но прыгать не стал, а поехал домой, зарегался на кодфорсе и стал изучать дп с битовыми масками. И вот когда он сдал задачу на контексте этой техникой, парень уверовал по настоящему и произошло чудо ОН ВСТАЛ И НАЧАЛ ХОДИТЬ!!! И стех пор никогда больше не болеет!