Всем спасибо за участие! Задачи следуют в порядке, в котором они шли на оригинальном соревновании.
562A - Логистические вопросы
(в трансляции: 566C - Логистические вопросы)
Формализуем задачу. Нам дано необычное определение расстояния по дереву: ρ(a, b) = dist(a, b)1.5. У каждой вершины есть её вес wi. Нужно как-то так выбрать место x для проведения соревнования, чтобы минимизировать сумму взвешенных расстояний от всех вершин до неё: f(x) = w1ρ(1, x) + w2ρ(x, 2) + ... + wnρ(x, n).
Давайте изучим свойства функции f(x). Мысленно разрешим себе ставить точку x не только в вершины дерева, но и в любую точку на ребре, доопределив естественным образом расстояние от точки внутри ребра до всех остальных вершин (например, середина ребра длины 4 находится на обычном расстоянии 2 от концов ребра).
Утверждение 1. На любом пути 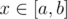 в дереве функция ρ(i, x) является выпуклой вниз. Действительно, функция dist(i, x) на любом пути выглядит как график функции abs(x), то есть сначала линейно убывает до ближайшей к i точки на пути [a, b], а потом линейно возрастает. Взяв композицию с выпуклой возрастающей функциея t1.5, как нетрудно видеть, мы снова получим выпуклую вниз на пути функцию. Здесь под функцией на пути мы подразумеваем обычную функцию действительной переменной x, где под x мы подразумеваем координату точки x на пути [a, b], или, что то же самое, dist(a, x). Таким образом, каждое из слагаемых в определении функции f(x) выпукло вниз на любом пути в дереве, а значит и функция f(x) выпукла на любом пути в дереве.
в дереве функция ρ(i, x) является выпуклой вниз. Действительно, функция dist(i, x) на любом пути выглядит как график функции abs(x), то есть сначала линейно убывает до ближайшей к i точки на пути [a, b], а потом линейно возрастает. Взяв композицию с выпуклой возрастающей функциея t1.5, как нетрудно видеть, мы снова получим выпуклую вниз на пути функцию. Здесь под функцией на пути мы подразумеваем обычную функцию действительной переменной x, где под x мы подразумеваем координату точки x на пути [a, b], или, что то же самое, dist(a, x). Таким образом, каждое из слагаемых в определении функции f(x) выпукло вниз на любом пути в дереве, а значит и функция f(x) выпукла на любом пути в дереве.
Будем называть функции, выпуклые вниз на любом пути в дереве выпуклыми на дереве. Сформулируем пару утверждений про выпуклые функции на дереве.
Утверждение 2. У выпуклой на дереве функции не может быть двух различных локальных минимумов. Действительно, в противном случае на пути между двумя этими минимумами функция сначала возрастает, а в конце убывает, что нарушает условие на выпуклость на этом пути.
Таким образом, у выпуклой вниз функции f(x) есть единственный локальный минимум на дереве, совпадающий с глобальным.
Утверждение 3. Из каждой вершины v дерева существует не более одного ребра, при движении по которому функция убывает. Действительно, в противном случае, если рассмотреть путь, образованный двумя такими рёбрами, то в точке, соответствующей вершине v, функция не будет выпукла вниз.
Назовём направление ребра из вершины v, при движении по которому убывает функция, градиентом функции f в точке x. Согласно утверждению 3, у выпуклой вниз функции f в любой вершине либо однозначно определён градиент, либо вершина является минимумом (глобальным).
Предположим, мы умеем некоторым образом эффективно искать направление градиента из вершины v. Научимся, пользуясь этим знанием и утверждениями 2 и 3 находить глобальный минимум. Если бы наше дерево представляло собой бамбук, то задача бы стала обычной одномерной задачей минимизации выпуклой функции, которая эффективно решается бинарным поиском, т. е. дихотомией. Нам же нужен некоторый эквивалент дихотомии на дереве. Что же это за эквивалент?
Воспользуемся centroid decmoposition! Действительно, возьмём центр дерева (т. е. такую вершину, что размеры всех её поддеревьев не превосходят n / 2). По утверждению 3 можно рассмотреть градиент функции в центре дерева. Во-первых, у функции может не оказаться градиента в центре дерева, что значит, что мы уже нашли оптимум. Иначе, мы знаем, что глобальный минимум расположен именно в поддереве в направлении градиента, значит все остальные поддеревья и сам центр можно выбросить из рассмотрения и оставить только выбранное поддерево. Таким образом, за один подсчёт градиента мы сократили в два раза количество вершин в рассматриваемой части дерева.
Значит, за  подсчётов градиента мы практически научились решать задачу. Осталось только понять, где именно расположен ответ. Заметим, что глобальный оптимум, скорее всего, окажется внутри какого-то ребра. Тогда, как нетрудно видеть, оптимальной вершиной является один из концов этого ребра, а именно, одна из двух последних рассмотренных в процессе нашего алгоритма вершин. В какой именно можно определить, явно вычислив значение функции в них и взяв меньшее.
подсчётов градиента мы практически научились решать задачу. Осталось только понять, где именно расположен ответ. Заметим, что глобальный оптимум, скорее всего, окажется внутри какого-то ребра. Тогда, как нетрудно видеть, оптимальной вершиной является один из концов этого ребра, а именно, одна из двух последних рассмотренных в процессе нашего алгоритма вершин. В какой именно можно определить, явно вычислив значение функции в них и взяв меньшее.
Теперь научимся считать направление градиента в вершине v. Зафиксируем одно поддерево ui вершины v. Рассмотрим производную всех слагаемых, соответствующих поддереву ui при движении в поддерево ui, и обозначим её за deri. Тогда, как нетрудно видеть, производная f(x) при движении от x = v в сторону поддерева ui есть - der1 - der2 - ... - deri - 1 + deri - deri + 1 - ... - derk, где k — степень вершины v. Таким образом, мы можем за один запуск обхода из вершины v определить все вершины deri, а значит, и направление градиента, найдя с помощью формулы выше направление, в котором производная функции отрицательна.
Таким образом, получилось решение за  .
.
562B - Клика в графе делителей
(в трансляции: 566F - Клика в графе делителей)
Упорядочим числа в искомой клике по возрастанию. Заметим, что чтобы множество X = {x1, ..., xk} образовывало клику, необходимо и достаточно, чтобы 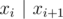 для (1 ≤ i ≤ k - 1). Таким образом, нетрудно сформулировать задачу динамического программирования: D[x] есть длина наибольшей подходящей возрастающей подпоследовательности, заканчивающейся в числе x. Формула пересчёта:
для (1 ≤ i ≤ k - 1). Таким образом, нетрудно сформулировать задачу динамического программирования: D[x] есть длина наибольшей подходящей возрастающей подпоследовательности, заканчивающейся в числе x. Формула пересчёта: 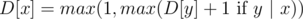 по всем x, лежащим в A.
по всем x, лежащим в A.
Если оформлять задачу динамического программирования в виде динамики "вперёд", то легко оценить сложность получившегося решения: в худшем случае количество переходов есть 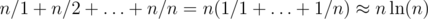 .
.
562C - Восстановление карты
(в трансляции: 566E - Восстановление карты)
Назовём окрестностью вершины — множество, состоящее из вершины и всех близких к ней вершин. Таким образом, нам известен набор окрестностей всех вершин в некотором произвольном порядке, причём каждая окрестность также перечислена в произвольном порядке.
Назовём вершину дерева внутренней, если она не является листом дерева. Аналогично, назовём ребро дерева внутренним, если оно соединяет две внутренних вершины. Заметим, что если две окрестности пересекаются ровно по двум элементам a и b, то a и b обязаны быть соединены ребром, причём ребро (a, b) является внутренним. Наоборот, любое внутреннее ребро (a, b) может быть найдено как пересечение каких-то двух окрестностей С и D двух вершин c и d, таких что в дереве есть путь c – a – b – d. Таким образом, мы можем найти все внутренние рёбра, рассмотрев попарные пересечения всех окрестностей. Это можно сделать за время порядка n3 / 2 наивно, либо в 32 раза быстрее, воспользовавшись битовым сжатием.
Заметим, что зная все внутренние рёбра, мы можем узнать все внутренние вершины, за исключением случая, когда граф представляет из себя звезду (т. е. вершину, к которой подцеплены все остальные). Случай звезды нужно разобрать отдельно.
Теперь мы знаем все листы, все внутренние вершины и структуру дерева на внутренних вершинах. Осталось только определить для каджого листа, к какой внутренней вершине он подцеплен. Это можно сделать следующим образом. Рассмотрим лист l. Рассмотрим все окрестности, его содержащие. Рассмотрим минимальную по включению окрестность — утверждается, что это есть окрестность L, соответствующая самому листу l. Рассмотрим все внутренние вершины в L. Их не может быть меньше двух. Если их три или более, то мы можем однозначно определить, к какой из них надо подцепить l — это должна быть та вершина из них, которая имеет степень внутри L больше единицы. Если же их ровно две (скажем, a и b), то определить, к кому из них надо подцепить l, несколько сложнее.
Утверждение: l должна быть подсоединена к той из двух вершин a и b, у которой степень по всем внутренним рёбрам — ровно один. Действительно, если бы l была подсоединена к вершине со внутренней степнью два или более, мы бы рассмотрели этот случай ранее.
Если же у обоих вершин a и b внутренняя степень — 1, то наш граф имеет вид гантели (ребро (a, b), и все остальные вершины, подцепленные либо за a, либо за b). Такой случай также придётся разобрать отдельно.
Разбор двух специальных случаев оставляется пытливому читателю как несложное упражнение.
562D - Реструктуризация компании
(в трансляции: 566D - Реструктуризация компании)
Эта задача допускает множество решений с разными асимптотиками. Опишем решение за 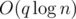 .
.
Рассмотрим сначала задачу, в которой присутствуют только запросы второго и третьего типа. Её можно решить следующим образом. Отметим всех работников в ряд на прямой от 1 до n. Заметим, что отделы представляют собой отрезки из подряд идущих работников. Будем поддерживать эти отрезки в любой логарифмической структуре данных, например в сбалансированном дереве поиска (std::set или TreeSet). Объединяя все отделы с позиции x по позицию y, вытаскиваем все отрезки, попавшие в диапазон [x, y] и сливаем их. Для ответа на запрос третьего типа проверяем, лежат ли работники x и y в одном отрезке. Таким образом, мы получаем решение более простой задачи за  на запрос.
на запрос.
Добавляя запросы первого типа мы на самом деле разрешаем некоторым отрезкам на прямой относиться к одному и тому же отделу. Добавим в решение систему непересекающихся множеств, которая будет поддерживать классы эквивалентности на отрезках. Теперь запросы первого типа можно реализовать как вызов merge в системе непересекающихся множеств от номеров отделов, к которым принадлежат сотрудники x и y. Также в запросах второго типа надо не забывать вызывать merge от всех удаляемых отрезков.
Получилось решение за время 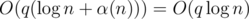 .
.
562E - Макс и Мин
(в трансляции: 566G - Макс и Мин)
Сформулируем задачу в геометрической интерпретации. У Макса и у Мина есть набор векторов из первой координатной четверти на плоскости и точка (x, y). За свой ход Макс может прибавить любой из имеющихся у него векторов к (x, y), а Мин — вычесть. Мин хочет добиться, чтобы точка (x, y) оказалась строго в третьей координатной четверти, Макс пытается ему помешать. Обозначим вектора Макса за Mxi, вектора Мина за Mnj.
Сформулируем очевидное достаточное условие для Макса, чтобы тот мог выиграть. Рассмотрим некоторое неотрицательное направление на плоскости, т. е. вектор (a, b), такой что a, b ≥ 0, при этом хотя бы одно из чисел a, b — не ноль. Тогда если среди ходов Макса есть такой вектор Mxi, что он не короче всех векторов Мина Mnj вдоль направления (a, b), то Макс может гарантировать себе победу. Здесь под длиной вектора v вдоль направления (a, b) подразумевается скалярное произведение вектора v на вектор (a, b).
Действительно, пусть Макс постоянно ходит в этот вектор Mxi. Тогда за пару ходов Макса и Мина точка (x, y) сдвинется на вектор Mxi - Mnj для некоторого j, а значит её сдвиг вдоль вектора (a, b) составит ((Mxi - Mnj), (a, b)) = (Mxi, (a, b)) - (Mnj, (a, b)) ≥ 0. Значит, так как исходно скалярное произведение ((x, y), (a, b)) = ax + by > 0, то и в любой момент времени ax + by будет строго положительно. А значит, Мин ни в какой момент времени не сможет добиться чтобы x и y стали оба отрицательными (так как это значило бы, что ax + by < 0).
Теперь сформулируем некоторый вариант обратного утверждения. Пусть вектор Макса Mxi лежит строго внутри треугольника, образованного векторами Мина Mnj и Mnk. При этом, вектор Mxi не может лежать на отрезке [Mnj, Mnk], но может быть коллинеарен одному из векторов Mnj и Mnk.
Заметим, что раз Mxi лежит строго внутри треугольника, натянутого на Mnj и Mnk, то его можно продлить до вектора Mx'i, конец которого лежит на отрезке [Mnj, Mnk]. В силу линейной зависимости Mx'i и Mnj, Mnk, имеем, что Mx'i = (p / r)Mnj + (q / r)Mnk, где p + q = r и p, q, r — целые неотрицательные числа. Это эквивалентно rMx'i = pMnj + qMnk, а значит, если на каждые r ходов Макса в Mxi мы будем отвечать p ходами Мина в Mnj и q ходами Мина в Mnk, то суммарный сдвиг составит - pMnj - qMnk + rMxi = - rMx'i + rMxi = - r(Mx'i - Mxi), то есть вектор со строго отрицательными компонентами. Таким образом, мы можем мажорировать данный ход Макса, т. е. он ему невыгоден.
Естественным образом возникает желание построить выпуклую оболочку на ходах Мина и посмотреть на все ходы Макса относительно неё. Если ход Макса лежит внутри выпуклой оболочки ходов Мина, то из предыдущего утверждения этот ход Максу невыгоден. В противном случае, возможно два варианта.
Либо этот ход пересекает выпуклую оболочку, но выходит из неё наружу — в таком случае этот ход Макса не короче всех ходов Мина в некотором неотрицательном направлении, а значит Макс победил.
Либо же, вектор Макса находится сбоку от выпуклой оболочки ходов Мина. Пусть для определённости вектор Mxi В таком случае, требуется отдельный анализ. Рассмотрим самый верхний из векторов Мина. Если вектор Mxi не ниже самого верхнего из ходов Макса Mxj, то по первому утверждению Макс может выиграть, ходя исключительно в этот вектор. В противном же случае, как несложно видеть, разность Mni - Mxj — это вектор со строго отрицательными компонентами, ходя в который мы можем мажорировать соответствующий вектор Макса.
Значит, полная версия критерия победы Мина выглядит следующим образом. Рассмотрим выпуклую оболочку ходов Мина и продлим её от самой верхней точки влево и от самой правой точки вниз. Если все ходы Макса попадают строго внутрь образованной фигуры, то Мин побеждает. Иначе побеждает Макс.
562F - Подбор имён
(в трансляции: 566A - Подбор имён)
Сформиурем бор из всех имён и псевдонимов. Отметим красным все вершины, соответствующие именам, и синим все вершины, соответствующие всем псевдонимам (одна вершина может быть отмечена несколько раз, в том числе разными цветами). Заметим, что если мы сопоставили имя a и псевдоним b, то качество такого сопоставления может быть выражено как lcp(a, b) = 1 / 2(2 * lcp(a, b)) = 1 / 2(|a| + |b| - (|a| - lcp(a, b)) - (|b| - lcp(a, b))), что представляет собой константу 1 / 2(|a| + |b|), из которой вычитается половина длины пути между a и b по бору. Таким образом, мы должны соединить все красные вершины с синими, минимизировав суммарную длину путей.
Нетрудно видеть, что такая задача решается жадным образом следующей рекурсивной процедурой: если у нас есть вершина v, в поддереве которой x красных вершин и y синих вершин, то мы должны сопоставить min(x, y) красных вершин этого поддерева синим вершинам, а оставшиеся max(x, y) - min(x, y) красных или синих вершин "отдать" на уровень выше. Корректность данного алгоритма легко объясняется следующим соображением. Ориентируем ребро каждого пути по направлению от красной вершины к синей. Если ребро получает две разных ориентации, то два пути, на которых оно лежит, легко "развести", уменьшив их суммарную длину.
Таким образом, получается несложное решение за O(sumlen), где sumlen — суммарная длина всех имён и псевдонимов.
562G - Репликация процессов
(в трансляции: 566B - Репликация процессов)
Эту задачу можно решить симулируя процесс реплицирования. Будем к каждому шагу поддерживать список всех репликаций, которые в текущий момент можно применить. Применяем любую репликацию, после чего обновляем список, добавляя/удаляя все подходящие или переставшие быть подходящими репликации со всех затронутых на данном шаге серверов. Список репликаций можно поддерживать в структуре данных "двусвязный список", которая позволяет за O(1) добавлять и удалять элемент в/из множества и вынимаь произвольный элемент множества.
Доказательство корректности этого алгоритма несложно и оставляется как упражнение (впрочем, если будет большое количество желающих, оно появится здесь позднее).
Получается решение за O(n) операций (впрочем, константа, скрытая за O-нотацией весьма немаленькая — один только ввод составляет 12n чисел, да и само решение оперирует по меньшей мере константой 36).













Автокомментарий: текст был обновлен пользователем Zlobober (предыдущая версия, новая версия, сравнить).
В 562G есть решение с очень простым доказательством, придуманное Petr'ом. Будем симулировать процесс с конца, поддерживая такой инвариант: в каждый момент времени есть не более одного сервера, у которого заняты все 9 слотов. Шаг делается так: если у всех серверов < занятых 9 слотов, делаем что угодно; иначе берём единственный 9-слотовый сервер, и применяем reverse-репликацию для любого из его процессов. В результате снова получится не более одного 9-слотового сервера.
Я бы послушал доказательство в g.
Сами мы в какой-то момент придумали то, что написал ilyakor, но не сдали т.к занимались другой задачей.
Очень легко решается, если посмотреть на процесс с конца. В конце можно делать любой ход, у нас в b и c -1, в а +1, если в a стало 9, значит, очевидно есть ход, который ещё не отменили, давайте следующим с конца ставить его, ну и так далее. [UPD] Ой, такое уже написали.
У меня есть доказательство для жадного алгоритма в прямом направлении, оно совсем не сложное, но я его напишу, наверное, уже завтра, а то время позднее и спать охота.
Буду благодарен.
Прошу прощения за задержку.
Давай для начала докажем в случае, когда нет репликации на один и тот же сервер. Будем говорить, что уровень сервера — это количество процессов на нём. Таким образом, у нас все сервера разбиваются по уровням от 0 до 9 включительно.
Нарисуем граф, соответствующий серверам, где для каждой оставшейся репликации из сервера a выходят рёбра в сервера b и c. Мы знаем, что репликацию можно произвести, если оба сервера b и c расположены на 8 уровне и ниже. Таким образом, для каждой из оставшихся репликаций хотя бы один из целевых серверов расположен на 9 уровне. Из этого следует, что есть хотя бы один сервер ровно 9 уровня (иначе у нас просто не осталось репликаций, а значит мы победили).
Оставим теперь в рассмотрении только сервера 9 уровня и все репликации, их затрагивающие. Применим разом все эти репликации — каждая из них либо понижает на один уровень максимум одного рассмотренного сервера (если он является a-сервером в репликации) и повышает на один уровень минимум одного, а может быть и двух серверов (соответственно b- и c- серверов этой репликации, т. к. среди них хотя бы один сервер обязательно 9 уровня). Таким образом, если применить разом все репликации, затрагивающие сервера 9 уровня, то суммарный уровень всех серверов 9 уровня не уменьшится, а в итоге он должен уменьшиться, так как в конце все эти сервера должны стать 8 уровня. Получаем противоречие.
В данное рассуждение не сильно сложно добавить случай, когда есть репликации на один и тот же сервер — достаточно аналогично рассмотреть в качестве потенциала сумму уровней всех серверов 8 и 9 уровня.
When you realize that problem Max and Min is a convex hull problem
В задаче F можно не писать бор, а отсортировать оба массива и запустить рекурсию на подотрезках(они будут соответсовать вершинам в боре как раз).
Возникает следующий вопрос: а будет ли работать сортировка массива за O(sumlen log smth). Довольно легко понять что mergesort и heapsort будут работать за O(sumlen log n). А правда ли это для quicksort? Ясно, что верхняя оценка не верна(как и у обычного qsorta), а правда ли что она верна для любого теста в среднем по выбору пивотов?
Ну а больше всего интересно, естественно, для std::sort aka introsort, но там как раз, вероятно, должно делаться из соображений про qsort+heapsort
Если quicksort обошёл k уровней, а сравнение строк шло за длину меньшей из них, очевидно, что каждый уровень был обработан за sumlen.
Да, согласен. Это как раз объяснить почему работает introsort(если я правильно понимаю, что он делает). Для куиксорта остаётся понять что уровней O(log n). Это вроде звучит правдоподобно
В задача "562G — Репликация процессов" с большим запасом прошел random_shuffle с последующим тупым многократным проходом в цикле по всем правилам и выполнением правил, не противоречащих условию.
Это всегда правильно работает и без random_shuffle.
Без шафла это точно должно работать за квадрат.
Более того, если не использовать собственную рандом-функцию в шафле, то такое решение тоже валится тестом:
(1 2 i%n) x 60000,(2 1 i%n) x 60000На счёт теста: если я его правильно понял, то он некорректен, так как каждый сервер должен встречаться в роли a, b и c O(1) раз.
Хм. Действительно.
А я вот как-то решал задачу, даже не заметив этого в условии:
А без этого ограничения задача не решаема? Или это просто упрощение?
Без этого условия не очень понятна постановка в целом. И не понятно, откуда взяться тому, что решение всегда существует.
Констната 4 скорее всего не существенна,и взята из реальности, хотя и модель ей не совсем соответствует. Задача родилась в процессе проведения достаточно похожей операции одним из админов компании.
For problem D — Restructuring Company the first solution coming to my mind was to use a Segment Tree supporting these operations:
Then create the tree of size N and for the operations:
This can be done with some kind of lazy propagation but I'm not sure if fits in the time limit.
P.S: I didn't take part in contest but I read this problem, I'll try to implement this solution when I have the time.
For problem D — Restructuring Company the first solution coming to my mind was to use a Segment Tree supporting these operations:
Then create the tree of size N and for the operations:
This can be done with some kind of lazy propagation but I'm not sure if fits in the time limit.
P.S: I didn't take part in contest but I read this problem, I'll try to implement this solution when I have the time.
Maybe I didn't get get your idea right, but I don't think it is going to work.
Try it on second sample. You have
1 2 3 4 5 6 7 8
at the beginning.
After first merge it becomes
1 2 3 4 2 6 7 8
Now second merge comes. If you are going to implement it in the way you described, your array will become:
1 2 3 4 4 4 4 8.
You have already lost information about 2 and 5 being in a same component — you repainted 5 with 4 after last query, but 2 remains painted with 2 (instead of being changed to 4 to remain same as 5).
Oh, you are right, I'm not sure if can be made some tricks to make it work but surely is overkill comparing with editorial solution.
Thanks, I only read the problem before going to take the lunch and build this idea while walking, never tried in paper or sample cases but I liked the problem.
What if we first query the range for the minimum value present(say x), and then update the range to x?
So here after second merge our answer will become(as minimum value is 2)
1 2 3 2 2 2 2 8
Now move to the next part of sample 2 and merge 1 with 2 :)
Now it is definitely an overkill. :P
for this part I thought about another infromation for every node called
bestwhere the best value for some range is the smallest parent of all elements parents and I'll propagate this information upward.
So for the sample input, the node with range [4,7] will have have it's best value equal to
2.Will this work ??
My idea has a little bit different to k790alex, I use DSU + Segment Tree(Lazy), when
I merge x and y the result is min of them. I using update to merge x,x+1,..y but when using DSU I can control the parent of them. I think it so perfect but it is wrong answer on test 3. My submission: 222029107
I'm not good at English, but I tried explain my idea, I want to contact to everybody. I'm sorry about that
It can be done with segment tree and DSU. No need for lazy propagation. Just keep array of visited nodes, so when you update an interval, you dont need to worry if some nodes below visited ones are already in the same group. Code.
Problem D can be solved in O(Q + (N * alpha(N))) . 12279157
Problem D, I use another method and passed all tests. And the time complexity seems to be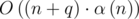 . Usa a array to mark the next index which elements is not in the same union, to deal with second type of query. So in the second type of query, every elements will just be merge once, so it is linear. 12278498
. Usa a array to mark the next index which elements is not in the same union, to deal with second type of query. So in the second type of query, every elements will just be merge once, so it is linear. 12278498
Ignore.
I tried simulating in Problem G — Replicating Processes but it is giving me WA. If you kept applying any arbitrary move that is possible as said in the editorial, we will fail sample test 1 itself.
An arbitrary order of valid moves in sample test 1 can look like this —
1 2 5 6 7 3
And this results in the final configuration being 7 processes for server 1 and 7 processes for server thus giving us a deadlock. So there is obviously something I am missing :/
Can someone please elaborate?
up to 9 processes at a single time, so both remaining operations are valid ( no deadlock ) ...
Ohh yeah missed that :P
So how do you prove this strategy then?Solved.
Why is it always possible to find a valid sequence of execution? I am unable to prove it. From what I could get from the editorial, given a sequence of steps we have already done, it is always possible to find a new rule which will be valid. Why is it so?
This is what I believe is the "proof" and it was enough to convince me.
Each server initially has 4 processes and each process will be replicated. Consider first the case where each replication is of the form A -> A, A. It is easy to see that in this case all replications can be carried out directly.
Now consider the case where we change one replication of the form A -> A, A to A -> A, B. This replication can also be carried out and now server B has 9 processes in its memory. But we know that in the final configuration, each server should contain exactly 8 processes in its memory. This means that one replication in B will change from B -> B, B to B -> B, X.
This will produce a chain reaction until we form a cycle. It is in fact guaranteed that a cycle will form since currently, server A has only 7 processes in its memory and it needs 8 so eventually we will get a cycle. Thus we can perform the replication by starting at any point in this cycle and finish the replication process. This argument can be extended to replications of the form A -> X, Y. Thus it is always possible to perform all the replication requests.
thanks for Editorial ;)
You'r welcome ;)
Are you Zlobober ?!! ;))
I have implemented algorithm mentioned in editorial for problem 'F. Clique in the Divisibility Graph' in Python which is getting TLE. But the same solution is accepted in Java. Is algorithm mentioned in editorial not applicable for Python?
Please find the link to find my submissions. Python: 12295295 Java: 12295231
Thanks in advance.
Accepted with Pypy. Typically, Python is slower than C++, and Pypy is faster than Python.
Thanks ItsLastDay. But does codeforces have different time limits for different programming languages like codechef?
As far as I know, on Codeforces time limits are the same for different languages.
In "Clique in the Divisibility Graph",what is meant by "xi | xi+1"?
| means "divides", so x_{i+1} is a multiple of x_i.
Почему моё решение С неверно? var N,i:longint; BEGIN read(N); for i:=1 to N-1 do writeln(i,' ',N); END.
Ведь я строю дерево,где все вершины близкие,что ВСЕГДА удовлетворяет входным данным (ведь по условию сказано о некоторой информации о близости, а не о том,что только данные из условия вершины близки). В моём случае ВСЕ вершины близки N-ой.
Почему моё решение С неверно?Потому что оно не для каждого теста строит решение, удовлетворяющее информации о близких дорогах.
ведь по условию сказано о некоторой информации о близости, а не о том,что только данные из условия вершины близкиДавайте посмотрим в условие: "Однако, информация о точном устройстве дорог в Древляндии была утеряна. Единственное, что могут использовать археологи — это сохранившуюся информацию о близких городах". Информация о близких дорогах полностью сохранилась у археологов, поэтому добавлять какой-то вершине иные близкие не разрешается.
Thanks for the editorial.
I don't understand something about solution of problem Logistical Question. Why do we use derivatives to find gradient direction? How can we get the formular of these derivatives?
Thanks.
It's well-known that function decreases if its derivative is negative. We don't have a derivative of a function in a point that is vertex of the tree in normal sence, but we have a one-sided derivative of its value when we move along some edge. Let's denote this derivative as .
.
Let's express value of f(x) as s1(x) + ... + sk(x) where s1, ..., sk are summands that are taken from each of the k subtrees of vertex v. Then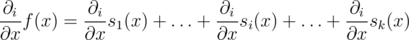 .
.
Let's denote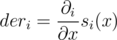 . Then it's easy to see that
. Then it's easy to see that  for j ≠ i (if when we move along the edge, the function decreases with some speed, then when we move to the other edge in the opposite direction, it will increase with the same speed). So, we get the formula from the editorial:
for j ≠ i (if when we move along the edge, the function decreases with some speed, then when we move to the other edge in the opposite direction, it will increase with the same speed). So, we get the formula from the editorial: 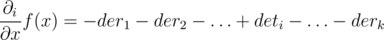 .
.
Thanks for your nice explaination. I got it now.
An alternative solution to problem 566E:
Define F(u, v) as the number of neighborhoods that contain both vertex u and vertex v. (u != v)
Observation: F(u, v) = 1 if and only if dist(u, v) = 4, F(u, v) = 2 if and only if dist(u, v) = 3 and F(u, v) > 2 if and only if dist(u, v) <= 2. (an exception: n = 2, this time we can simply output "1, 2") Using bitsets, we can easily find all F(u, v)s in O(n^3 / w) time so that we know all pairs of vertices that have a distance 3 or 4, which forms a weighted graph G.
Let the diameter of the tree be D.
D is 2(D can't be 1 for n > 2) if and only if G has no edges. In this situation, we can output any tree of diameter 2.
D is 3 if and only if G has some edge(s) of weight 3 but no edges of weight 4. Then G must be a complete bipartite graph plus 2 isolated vertices. The order of the isolated vertices doesn't matter.
Otherwise:
Let a vertex be black if its distance to 1 is even, and white if it's not black.
D is 4 if and only if G has 1 connected component plus an isolated vertex. The latter vertex must be the center, and its color should be the same as that of the diameter's endpoint.
If D is larger than 4, G is connected and it's easy to determine the color of each vertex.
After coloring each vertex, it's easy to figure out that two vertices u and v are connected if and only if F(u, v) >2 and u and v are in different colors.
Total complexity: O(n^3 / w)
This can also be used to check whether it's possible to satisfy the constraints.