Tribbiani's blog

221D — Little Elephant and Array
By Tribbiani, history, 9 years ago, In English

I've solved this problem using sqrt decomposition. but how can i solve it using segment tree?

Thanks in advance :)

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You can solve this problem without sqrt decomposition and segment tree. See this 11088217 submission

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

That solution uses the idea that since we're asking for all numbers x that have at least x occurences, and the maximum number of elements is 105, the maximum amount of such numbers is 446, because .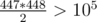

While it's not Mo's algorithm or dividing the queries into buckets, it's still based on the concept of square root.

→ Reply